Question Number 152532 by mondli66 last updated on 29/Aug/21
Answered by amin96 last updated on 29/Aug/21
$$\begin{cases}{\mathrm{0}+{y}+\mathrm{3}{z}=−\mathrm{4}}\\{{x}+\mathrm{2}{y}+{z}=\mathrm{7}}\\{{x}−\mathrm{2}{y}+\mathrm{0}=\mathrm{1}}\end{cases}\:\:\:\Rightarrow\:\:\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{7}}\\{\mathrm{1}}&{−\mathrm{2}}&{\mathrm{0}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{1}}&{\mathrm{3}}&{−\mathrm{4}}\end{pmatrix}^{\left(\mathrm{1}\right)−\left(\mathrm{1}\right)} = \\ $$$$=\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{7}}\\{\mathrm{0}}&{\mathrm{4}}&{\mathrm{1}}&{\mathrm{6}}\\{\mathrm{0}}&{\mathrm{1}}&{\mathrm{3}}&{−\mathrm{4}}\end{pmatrix}^{\left(\mathrm{3}\right)×\mathrm{4}−\left(\mathrm{2}\right)} =\begin{pmatrix}{\mathrm{1}}&{\mathrm{2}}&{\mathrm{1}}&{\mathrm{7}}\\{\mathrm{0}}&{\mathrm{4}}&{\mathrm{1}}&{\mathrm{6}}\\{\mathrm{0}}&{\mathrm{0}}&{\mathrm{11}}&{−\mathrm{22}}\end{pmatrix} \\ $$$$\begin{cases}{{x}+\mathrm{2}{y}+{z}=\mathrm{7}}\\{\mathrm{4}{y}+{z}=\mathrm{6}}\\{\mathrm{11}{z}=−\mathrm{22}}\end{cases}\:\:\Rightarrow\:{z}=−\mathrm{2}\:\Rightarrow\:{y}=\mathrm{2}\:\:\Rightarrow{x}=\mathrm{5} \\ $$$${answer}\:\:\:\left(\mathrm{5};\:\mathrm{2}\:;\:−\mathrm{2}\right) \\ $$$$ \\ $$
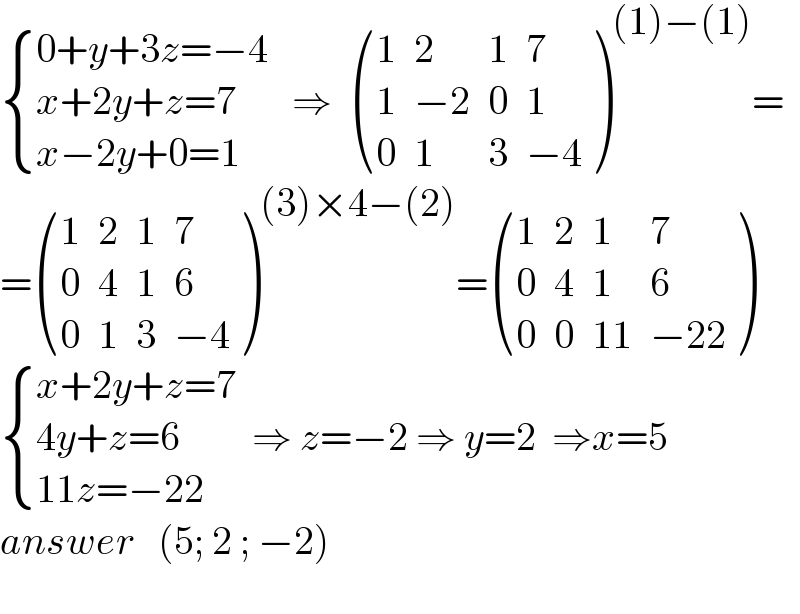
Commented by amin96 last updated on 29/Aug/21
$${Gauss}\:{method} \\ $$
Commented by SANOGO last updated on 29/Aug/21
Commented by KONE last updated on 29/Aug/21
![K=∫_(1/2) ^2 (1+(1/x^2 ))arctan(x)dx posont t=(1/x)⇔dx=−(1/t^2 )dt x=2⇔t=(1/2); x=(1/2)⇔t=2 K=∫_2 ^(1/2) (1+t^2 )arctan((1/t))×(−(1/t^2 ))dt =∫_(1/2) ^2 (1+(1/t^2 ))arctan((1/t))dt 2K=∫_(1/2) ^2 (1+(1/x^2 ))arctan(x)dx+∫_(1/2) ^2 (1+(1/t^2 ))arctan((1/t))dt =∫_(1/2) ^2 (1+(1/x^2 ))(arctan(x)+arctan((1/x)))dx car x et t son muette on sait que x>0 arctan(x)+arctan((1/x))=(Π/2) d′ou 2K=(Π/2)∫_(1/2) ^2 (1+(1/x^2 ))dx K=(Π/4)[x−(1/x)]_(1/2) ^2 =(Π/4)[2−(1/2)−(1/2)+2] K=((3Π)/4) KAB](Q152569.png)
$${K}=\int_{\mathrm{1}/\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){arctan}\left({x}\right){dx} \\ $$$${posont}\:{t}=\frac{\mathrm{1}}{{x}}\Leftrightarrow{dx}=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{dt} \\ $$$${x}=\mathrm{2}\Leftrightarrow{t}=\frac{\mathrm{1}}{\mathrm{2}};\:\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\Leftrightarrow{t}=\mathrm{2} \\ $$$${K}=\int_{\mathrm{2}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right){arctan}\left(\frac{\mathrm{1}}{{t}}\right)×\left(−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){dt} \\ $$$$=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){arctan}\left(\frac{\mathrm{1}}{{t}}\right){dt} \\ $$$$\mathrm{2}{K}=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){arctan}\left({x}\right){dx}+\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right){arctan}\left(\frac{\mathrm{1}}{{t}}\right){dt} \\ $$$$=\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\left({arctan}\left({x}\right)+{arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right){dx}\:{car}\:{x}\:{et}\:{t}\:{son}\:{muette} \\ $$$${on}\:{sait}\:{que}\:{x}>\mathrm{0}\:\:{arctan}\left({x}\right)+{arctan}\left(\frac{\mathrm{1}}{{x}}\right)=\frac{\Pi}{\mathrm{2}} \\ $$$${d}'{ou}\:\mathrm{2}{K}=\frac{\Pi}{\mathrm{2}}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right){dx} \\ $$$${K}=\frac{\Pi}{\mathrm{4}}\left[{x}−\frac{\mathrm{1}}{{x}}\right]_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{2}} =\frac{\Pi}{\mathrm{4}}\left[\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}\right] \\ $$$${K}=\frac{\mathrm{3}\Pi}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\underline{\mathscr{KAB}} \\ $$