
Question and Answers Forum
Question Number 152588 by rexford last updated on 30/Aug/21
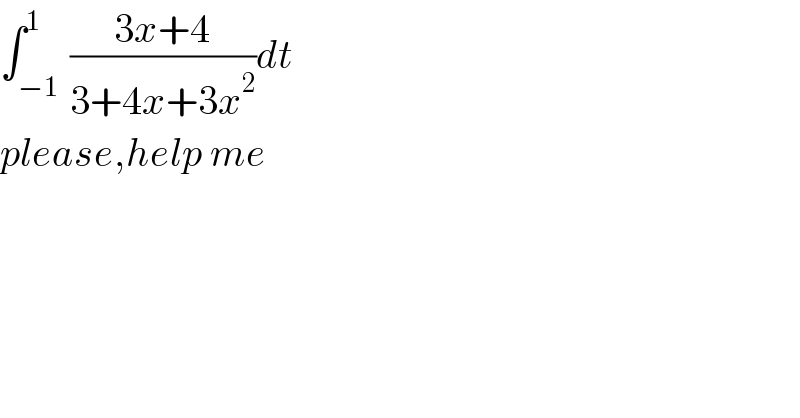
Answered by qaz last updated on 30/Aug/21
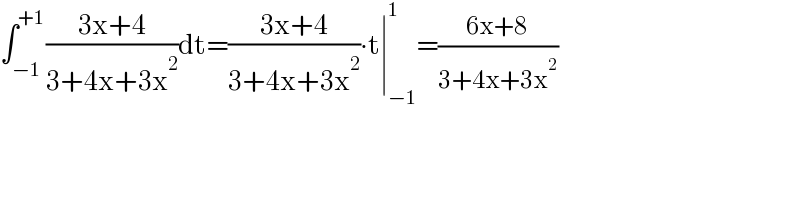
Answered by puissant last updated on 30/Aug/21
![=(1/2)∫_(−1) ^1 ((6x+4+4)/(3x^2 +4x+3))dx = (1/2)∫_(−1) ^1 ((6x+4)/(3x^2 +4x+3))dx+(2/3)∫_(−1) ^(+1) (1/(x^2 +(4/3)x+1))dx =(1/2)[ln∣3x^2 +4x+3∣]_(−1) ^1 +(2/3)Q =(1/2)ln5+(2/3)Q Q=∫_(−1) ^1 (1/(x^2 +(4/3)x+1))dx = ∫_(−1) ^1 (1/((x+(2/3))^2 −(4/9)+(9/9)))dx =∫_(−1) ^1 (1/((x+(2/3))^2 +(5/9)))dx =(9/5)∫_(−1) ^1 (1/([((3/( (√5)))(x+(2/3)))^2 +1]))dx u=(3/( (√5)))(x+(2/3)) → dx=((√5)/3)du ⇒ Q=(9/5)×((√5)/3)∫_(−1) ^1 (1/(u^2 +1))du =(3/( (√5)))[arctan(u)]_(−1) ^1 = (3/( (√5)))×(π/2). ∴∵ I=(1/2)ln5+(3/( (√5)))×(2/3)×(π/2) = (1/2)ln5+(π/( (√5)))..](Q152589.png)
Answered by phanphuoc last updated on 30/Aug/21
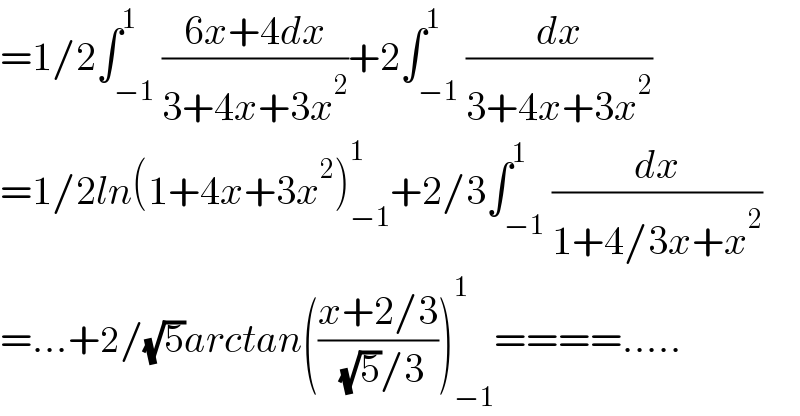
| ||
Question and Answers Forum | ||
Question Number 152588 by rexford last updated on 30/Aug/21 | ||
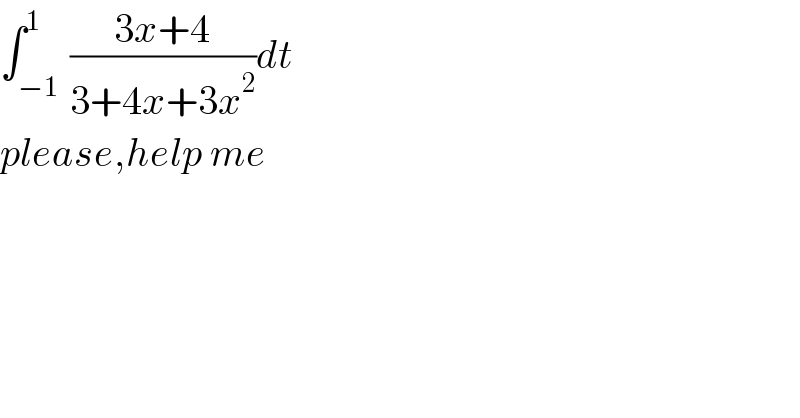 | ||
Answered by qaz last updated on 30/Aug/21 | ||
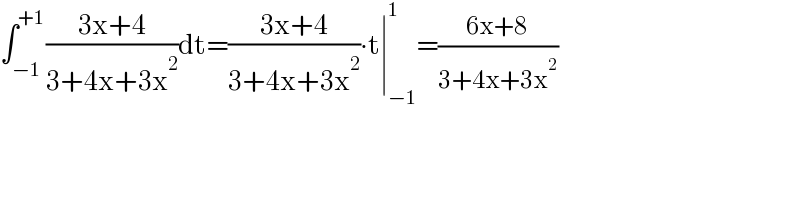 | ||
| ||
Answered by puissant last updated on 30/Aug/21 | ||
![=(1/2)∫_(−1) ^1 ((6x+4+4)/(3x^2 +4x+3))dx = (1/2)∫_(−1) ^1 ((6x+4)/(3x^2 +4x+3))dx+(2/3)∫_(−1) ^(+1) (1/(x^2 +(4/3)x+1))dx =(1/2)[ln∣3x^2 +4x+3∣]_(−1) ^1 +(2/3)Q =(1/2)ln5+(2/3)Q Q=∫_(−1) ^1 (1/(x^2 +(4/3)x+1))dx = ∫_(−1) ^1 (1/((x+(2/3))^2 −(4/9)+(9/9)))dx =∫_(−1) ^1 (1/((x+(2/3))^2 +(5/9)))dx =(9/5)∫_(−1) ^1 (1/([((3/( (√5)))(x+(2/3)))^2 +1]))dx u=(3/( (√5)))(x+(2/3)) → dx=((√5)/3)du ⇒ Q=(9/5)×((√5)/3)∫_(−1) ^1 (1/(u^2 +1))du =(3/( (√5)))[arctan(u)]_(−1) ^1 = (3/( (√5)))×(π/2). ∴∵ I=(1/2)ln5+(3/( (√5)))×(2/3)×(π/2) = (1/2)ln5+(π/( (√5)))..](Q152589.png) | ||
| ||
Answered by phanphuoc last updated on 30/Aug/21 | ||
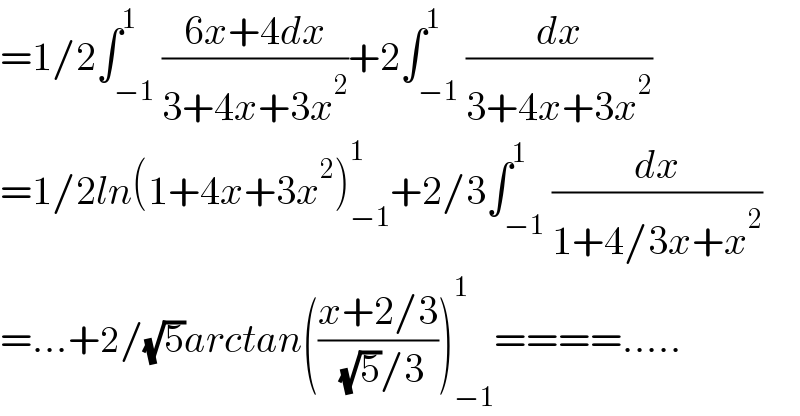 | ||
| ||