Question Number 15301 by Tinkutara last updated on 09/Jun/17
$$\mathrm{With}\:\mathrm{the}\:\mathrm{help}\:\mathrm{of}\:\mathrm{graph},\:\mathrm{find}\:\mathrm{the} \\ $$ $$\mathrm{solution}\:\mathrm{set}\:\mathrm{of}\:\mathrm{inequation}\:\mathrm{tan}\:{x}\:>\:−\sqrt{\mathrm{3}}\:. \\ $$
Answered by mrW1 last updated on 09/Jun/17
$$\mathrm{x}\in\left(\mathrm{n}\pi−\frac{\pi}{\mathrm{3}},\:\mathrm{n}\pi+\frac{\pi}{\mathrm{2}}\right)\:\wedge\:\mathrm{n}\in\mathbb{Z} \\ $$
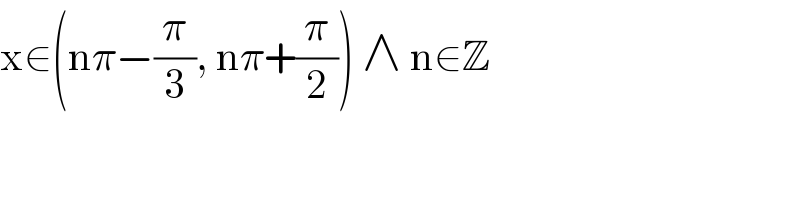
Commented byTinkutara last updated on 10/Jun/17
![But answer is [nπ − (π/3) < x < nπ + (π/2)] ∪ {nπ + ((2π)/3) < x < nπ + ((3π)/2)} Your first set is correct but how to get the 2^(nd) set in union?](Q15394.png)
$$\mathrm{But}\:\mathrm{answer}\:\mathrm{is}\:\left[{n}\pi\:−\:\frac{\pi}{\mathrm{3}}\:<\:{x}\:<\:{n}\pi\:+\:\frac{\pi}{\mathrm{2}}\right] \\ $$ $$\cup\:\left\{{n}\pi\:+\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:<\:{x}\:<\:{n}\pi\:+\:\frac{\mathrm{3}\pi}{\mathrm{2}}\right\} \\ $$ $$\mathrm{Your}\:\mathrm{first}\:\mathrm{set}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{but}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get} \\ $$ $$\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{set}\:\mathrm{in}\:\mathrm{union}? \\ $$
Commented bymrW1 last updated on 10/Jun/17
$$\mathrm{the}\:\mathrm{second}\:\mathrm{set}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{the}\:\mathrm{first}. \\ $$ $$\:\left\{{n}\pi\:+\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:<\:{x}\:<\:{n}\pi\:+\:\frac{\mathrm{3}\pi}{\mathrm{2}}\right\} \\ $$ $$\equiv\left\{\left(\mathrm{n}+\mathrm{1}\right)\pi−\frac{\pi}{\mathrm{3}}<\mathrm{x}<\left(\mathrm{n}+\mathrm{1}\right)\pi+\frac{\pi}{\mathrm{2}}\right\} \\ $$ $$\equiv\left\{\mathrm{m}\pi−\frac{\pi}{\mathrm{3}}<\mathrm{x}<\mathrm{m}\pi+\frac{\pi}{\mathrm{2}}\right\} \\ $$ $$\mathrm{since}\:\mathrm{n}\:\in\:\mathbb{Z},\:\mathrm{in}\:\mathrm{set}\:\mathrm{1}\:\mathrm{is}\:\mathrm{set}\:\mathrm{2}\:\mathrm{included}. \\ $$
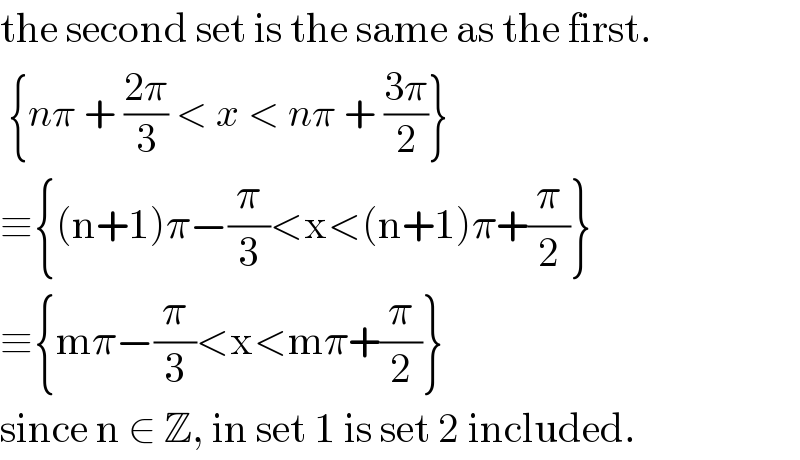
Commented byTinkutara last updated on 10/Jun/17
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$