
Question and Answers Forum
Question Number 173424 by mnjuly1970 last updated on 11/Jul/22
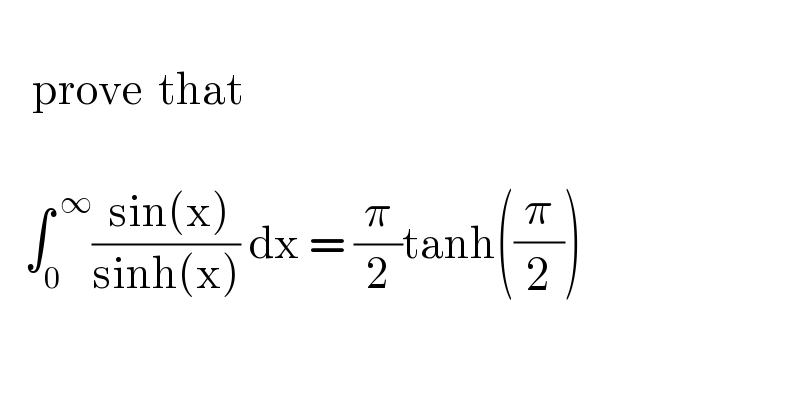
Answered by Mathspace last updated on 11/Jul/22
![Ψ=∫_0 ^∞ ((sinx)/(sh(x)))dx=2∫_0 ^∞ ((sinx)/(e^x −e^(−x) ))dx =2∫_0 ^∞ ((e^(−x) sinx)/(1−e^(−2x) ))dx =2∫_0 ^∞ e^(−x) sinxΣ_(n=0) ^∞ e^(−2nx) dx =2Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(2n+1)x) sinx dx but ∫_0 ^∞ e^(−(2n+1)x) sinxdx =Im(∫_0 ^∞ e^(−(n+1)x+ix) dx) and ∫_0 ^∞ e^(−(n+1)+i)x) dx =(1/(−(n+1)+i))e^(−(n+1)+i)x) ]_0 ^∞ =(1/(n+1−i))=((n+1+i)/((n+1)^2 +1)) ⇒ Im(∫_0 ^∞ ....)=(1/((n+1)^2 +1)) ⇒ Ψ=2Σ_(n=0) ^∞ (1/((n+1)^2 +1)) =2Σ_(n=1) ^∞ (1/(n^2 +1)) Σ_(n=0) ^∞ (1/(n^2 +1))=Σ_(n=0) ^∞ (1/((n+i)(n−i))) =((Ψ(i)−Ψ(−i))/(2i)) after we use Ψ(z)−Ψ(1−z)=πcotan(πz) or we can developp cos(αx) at fourier serie to find the value...](Q173427.png)
Commented by mnjuly1970 last updated on 11/Jul/22

Commented by Tawa11 last updated on 13/Jul/22

| ||
Question and Answers Forum | ||
Question Number 173424 by mnjuly1970 last updated on 11/Jul/22 | ||
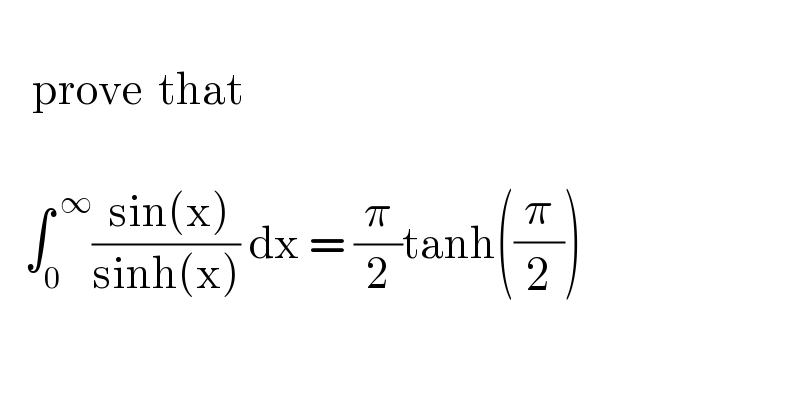 | ||
Answered by Mathspace last updated on 11/Jul/22 | ||
![Ψ=∫_0 ^∞ ((sinx)/(sh(x)))dx=2∫_0 ^∞ ((sinx)/(e^x −e^(−x) ))dx =2∫_0 ^∞ ((e^(−x) sinx)/(1−e^(−2x) ))dx =2∫_0 ^∞ e^(−x) sinxΣ_(n=0) ^∞ e^(−2nx) dx =2Σ_(n=0) ^∞ ∫_0 ^∞ e^(−(2n+1)x) sinx dx but ∫_0 ^∞ e^(−(2n+1)x) sinxdx =Im(∫_0 ^∞ e^(−(n+1)x+ix) dx) and ∫_0 ^∞ e^(−(n+1)+i)x) dx =(1/(−(n+1)+i))e^(−(n+1)+i)x) ]_0 ^∞ =(1/(n+1−i))=((n+1+i)/((n+1)^2 +1)) ⇒ Im(∫_0 ^∞ ....)=(1/((n+1)^2 +1)) ⇒ Ψ=2Σ_(n=0) ^∞ (1/((n+1)^2 +1)) =2Σ_(n=1) ^∞ (1/(n^2 +1)) Σ_(n=0) ^∞ (1/(n^2 +1))=Σ_(n=0) ^∞ (1/((n+i)(n−i))) =((Ψ(i)−Ψ(−i))/(2i)) after we use Ψ(z)−Ψ(1−z)=πcotan(πz) or we can developp cos(αx) at fourier serie to find the value...](Q173427.png) | ||
| ||
Commented by mnjuly1970 last updated on 11/Jul/22 | ||
 | ||
Commented by Tawa11 last updated on 13/Jul/22 | ||
 | ||