Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 153162 by mathdanisur last updated on 05/Sep/21

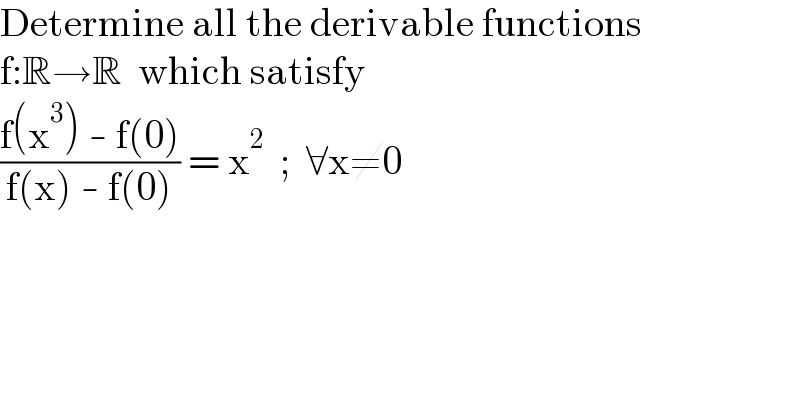
Determine all the derivable functions f:R→R which satisfy ((f(x^3 ) - f(0))/(f(x) - f(0))) = x^2 ; ∀x≠0

$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{the}\:\mathrm{derivable}\:\mathrm{functions} \\ $$$$\mathrm{f}:\mathbb{R}\rightarrow\mathbb{R}\:\:\mathrm{which}\:\mathrm{satisfy} \\ $$$$\frac{\mathrm{f}\left(\mathrm{x}^{\mathrm{3}} \right)\:-\:\mathrm{f}\left(\mathrm{0}\right)}{\mathrm{f}\left(\mathrm{x}\right)\:-\:\mathrm{f}\left(\mathrm{0}\right)}\:=\:\mathrm{x}^{\mathrm{2}} \:\:;\:\:\forall\mathrm{x}\neq\mathrm{0} \\ $$

Answered by aleks041103 last updated on 05/Sep/21

let g(x)=f(x)−f(0) g(x^3 )=x^2 g(x)⇒((g(x^3 ))/x^3 )=((g(x))/x) let h(x)=g(x)/x=((f(x)−f(0))/x) h(x^3 )=h(x) by induction h(x)=h(x^3^n )=h(x^3^(−n) ), for ∀n∈N let 1>ε>0. case 1: x∈(0,1) we can always find some n such that 1>a=x^3^(−n) >1−ε Then for ∀x∈(0,1) and any 1>ε>0, exists a number a∈[1−ε,1) such that h(x)=h(a). Since we can take ε to be arbitrairly small, then h(x)=lim_(ε→0) h(1>a>1−ε) Since f(x) is differentiable, then h(x) is too(for x≠0) and so h is continuous ⇒h(x∈(0,1))=lim_(ε→0) h(1>a>1−ε)=h(1). case 2: x∈(1,∞) by analogy, we can always find n such that x^3^(−n) ∈(1,1+ε). Then again h(x>1)=lim_(ε→0) h(1<a<1+ε)=h(1) Conclusion: h(x>0)=h(1)=a=const. Analogously one can prove h(x<0)=h(−1)=b=const. Then f(x)= { ((ax+f(0), x≥0)),((bx+f(0), x<0)) :} But for f(x) to be diff. at x=0 we need a=b. ⇒f(x)=ax+f(0) is the only solution!

$${let}\:{g}\left({x}\right)={f}\left({x}\right)−{f}\left(\mathrm{0}\right) \\ $$$${g}\left({x}^{\mathrm{3}} \right)={x}^{\mathrm{2}} {g}\left({x}\right)\Rightarrow\frac{{g}\left({x}^{\mathrm{3}} \right)}{{x}^{\mathrm{3}} }=\frac{{g}\left({x}\right)}{{x}} \\ $$$${let}\:{h}\left({x}\right)={g}\left({x}\right)/{x}=\frac{{f}\left({x}\right)−{f}\left(\mathrm{0}\right)}{{x}} \\ $$$${h}\left({x}^{\mathrm{3}} \right)={h}\left({x}\right) \\ $$$${by}\:{induction} \\ $$$${h}\left({x}\right)={h}\left({x}^{\mathrm{3}^{{n}} } \right)={h}\left({x}^{\mathrm{3}^{−{n}} } \right),\:{for}\:\forall{n}\in\mathbb{N} \\ $$$${let}\:\mathrm{1}>\varepsilon>\mathrm{0}. \\ $$$$\boldsymbol{{c}}{ase}\:\mathrm{1}:\:{x}\in\left(\mathrm{0},\mathrm{1}\right) \\ $$$${we}\:{can}\:{always}\:{find}\:{some}\:{n}\:{such}\:{that} \\ $$$$\mathrm{1}>{a}={x}^{\mathrm{3}^{−{n}} } >\mathrm{1}−\varepsilon \\ $$$${Then}\:{for}\:\forall{x}\in\left(\mathrm{0},\mathrm{1}\right)\:{and}\:{any}\:\mathrm{1}>\varepsilon>\mathrm{0},\: \\ $$$${exists}\:{a}\:{number}\:{a}\in\left[\mathrm{1}−\varepsilon,\mathrm{1}\right)\:{such}\:{that} \\ $$$${h}\left({x}\right)={h}\left({a}\right). \\ $$$${Since}\:{we}\:{can}\:{take}\:\varepsilon\:{to}\:{be}\:{arbitrairly} \\ $$$${small},\:{then} \\ $$$${h}\left({x}\right)=\underset{\varepsilon\rightarrow\mathrm{0}} {\mathrm{lim}}\:{h}\left(\mathrm{1}>{a}>\mathrm{1}−\varepsilon\right) \\ $$$${Since}\:{f}\left({x}\right)\:{is}\:{differentiable},\:{then}\:{h}\left({x}\right) \\ $$$${is}\:{too}\left({for}\:{x}\neq\mathrm{0}\right)\:{and}\:{so}\:{h}\:{is}\:{continuous} \\ $$$$\Rightarrow{h}\left({x}\in\left(\mathrm{0},\mathrm{1}\right)\right)=\underset{\varepsilon\rightarrow\mathrm{0}} {\mathrm{lim}}\:{h}\left(\mathrm{1}>{a}>\mathrm{1}−\varepsilon\right)={h}\left(\mathrm{1}\right). \\ $$$$\boldsymbol{{case}}\:\mathrm{2}:\:\boldsymbol{{x}}\in\left(\mathrm{1},\infty\right) \\ $$$${by}\:{analogy},\:{we}\:{can}\:{always}\:{find}\:{n}\:{such}\:{that} \\ $$$${x}^{\mathrm{3}^{−{n}} } \in\left(\mathrm{1},\mathrm{1}+\varepsilon\right). \\ $$$${Then}\:{again} \\ $$$${h}\left({x}>\mathrm{1}\right)=\underset{\varepsilon\rightarrow\mathrm{0}} {\mathrm{lim}}\:{h}\left(\mathrm{1}<{a}<\mathrm{1}+\varepsilon\right)={h}\left(\mathrm{1}\right) \\ $$$$\boldsymbol{{Conclusion}}: \\ $$$${h}\left({x}>\mathrm{0}\right)={h}\left(\mathrm{1}\right)={a}={const}. \\ $$$$ \\ $$$${Analogously}\:{one}\:{can}\:{prove} \\ $$$${h}\left({x}<\mathrm{0}\right)={h}\left(−\mathrm{1}\right)={b}={const}. \\ $$$$ \\ $$$${Then} \\ $$$${f}\left({x}\right)=\begin{cases}{{ax}+{f}\left(\mathrm{0}\right),\:{x}\geqslant\mathrm{0}}\\{{bx}+{f}\left(\mathrm{0}\right),\:{x}<\mathrm{0}}\end{cases} \\ $$$${But}\:{for}\:{f}\left({x}\right)\:{to}\:{be}\:{diff}.\:{at}\:{x}=\mathrm{0}\:{we}\:{need} \\ $$$${a}={b}. \\ $$$$\Rightarrow{f}\left({x}\right)={ax}+{f}\left(\mathrm{0}\right)\:{is}\:{the}\:{only}\:{solution}! \\ $$

Commented by mathdanisur last updated on 06/Sep/21

Thank you ser nice

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{ser}\:\mathrm{nice} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com