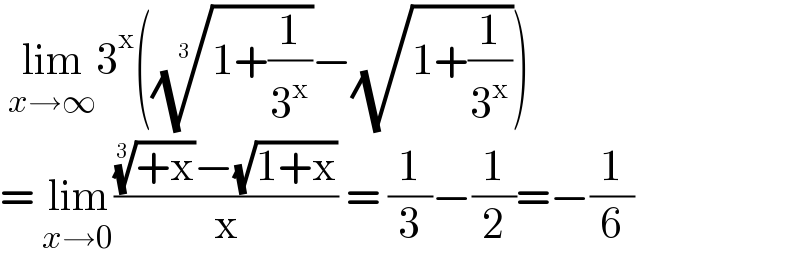Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 153352 by liberty last updated on 06/Sep/21

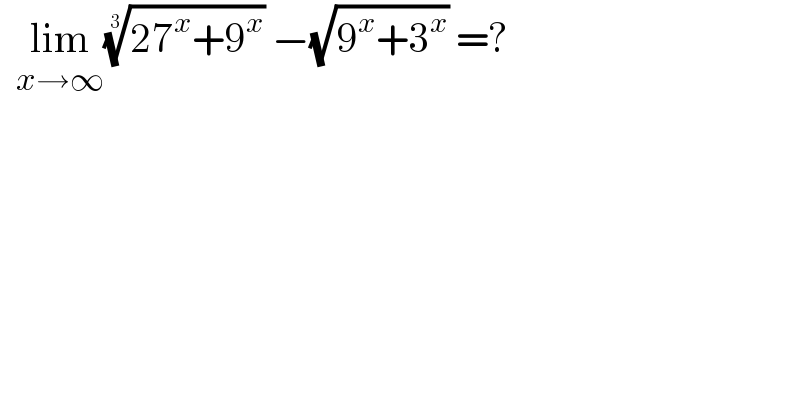
lim_(x→∞) ((27^x +9^x ))^(1/3) −(√(9^x +3^x )) =?

$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{3}}]{\mathrm{27}^{{x}} +\mathrm{9}^{{x}} }\:−\sqrt{\mathrm{9}^{{x}} +\mathrm{3}^{{x}} }\:=? \\ $$

Answered by MJS_new last updated on 06/Sep/21

lim_(x→+∞) (27^x +9^x )^(1/3) −(9^x +3^x )^(1/2) = [x=−((ln t)/(ln 3)) → t→0^+ ] =lim_(t→0^+ ) (((t+1)^(1/3) −(t+1)^(1/2) )/t) = [L′Ho^� pital] =lim_(t→0^+ ) ((2−3(t+1)^(1/6) )/(6(t+1)^(2/3) )) =−(1/6)

$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\left(\mathrm{27}^{{x}} +\mathrm{9}^{{x}} \right)^{\mathrm{1}/\mathrm{3}} −\left(\mathrm{9}^{{x}} +\mathrm{3}^{{x}} \right)^{\mathrm{1}/\mathrm{2}} \:= \\ $$$$\:\:\:\:\:\left[{x}=−\frac{\mathrm{ln}\:{t}}{\mathrm{ln}\:\mathrm{3}}\:\rightarrow\:{t}\rightarrow\mathrm{0}^{+} \right] \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\left({t}+\mathrm{1}\right)^{\mathrm{1}/\mathrm{3}} −\left({t}+\mathrm{1}\right)^{\mathrm{1}/\mathrm{2}} }{{t}}\:= \\ $$$$\:\:\:\:\:\left[\mathrm{L}'\mathrm{H}\hat {\mathrm{o}pital}\right] \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{2}−\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{1}/\mathrm{6}} }{\mathrm{6}\left({t}+\mathrm{1}\right)^{\mathrm{2}/\mathrm{3}} }\:=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Commented by liberty last updated on 06/Sep/21

yes sir

$${yes}\:{sir} \\ $$

Commented by MJS_new last updated on 06/Sep/21

��

Commented by liberty last updated on 06/Sep/21

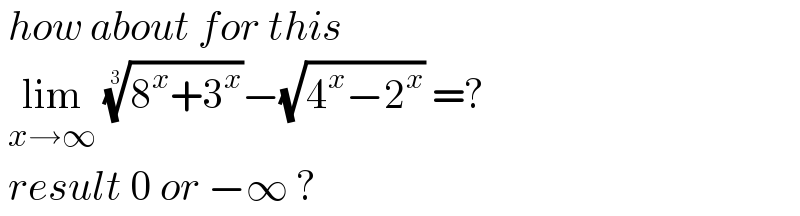
how about for this lim_(x→∞) ((8^x +3^x ))^(1/3) −(√(4^x −2^x )) =? result 0 or −∞ ?

$$\:{how}\:{about}\:{for}\:{this}\: \\ $$$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}}]{\mathrm{8}^{{x}} +\mathrm{3}^{{x}} }−\sqrt{\mathrm{4}^{{x}} −\mathrm{2}^{{x}} }\:=? \\ $$$$\:{result}\:\mathrm{0}\:{or}\:−\infty\:? \\ $$

Commented by MJS_new last updated on 07/Sep/21

it seems to be (1/2)

$$\mathrm{it}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{be}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by liberty last updated on 07/Sep/21

yes sir

$${yes}\:{sir} \\ $$

Answered by liberty last updated on 06/Sep/21

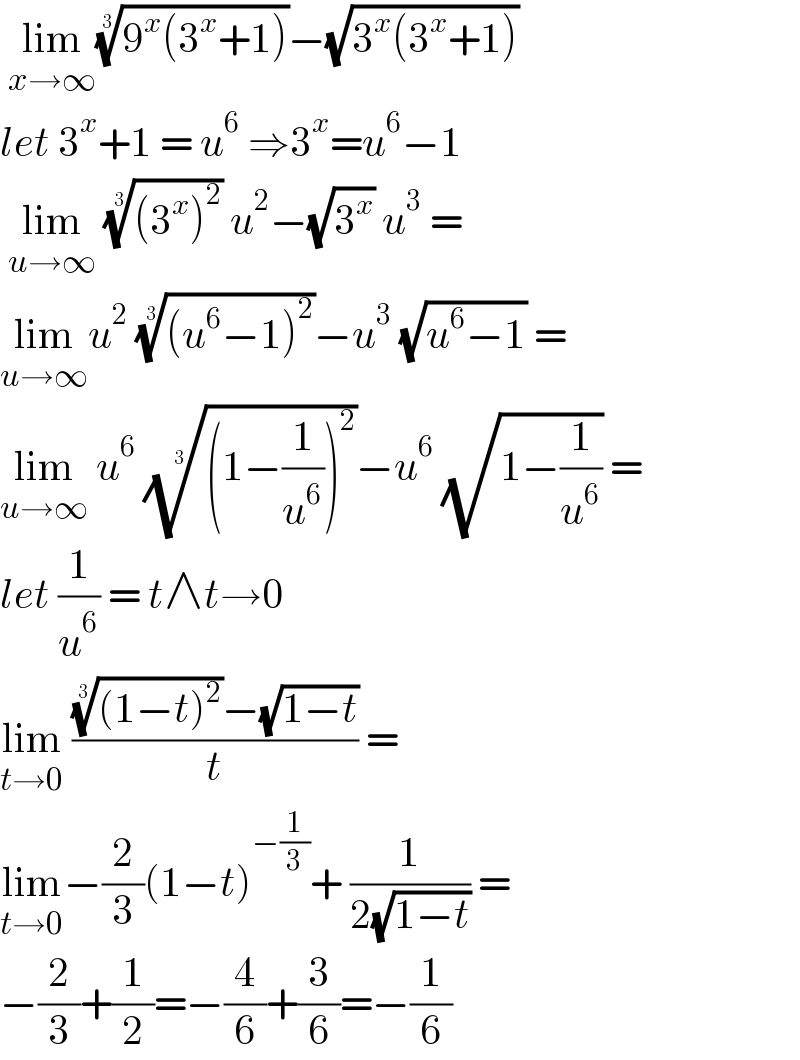
lim_(x→∞) ((9^x (3^x +1)))^(1/3) −(√(3^x (3^x +1))) let 3^x +1 = u^6 ⇒3^x =u^6 −1 lim_(u→∞) (((3^x )^2 ))^(1/3) u^2 −(√3^x ) u^3 = lim_(u→∞) u^2 (((u^6 −1)^2 ))^(1/3) −u^3 (√(u^6 −1)) = lim_(u→∞) u^6 (((1−(1/u^6 ))^2 ))^(1/3) −u^6 (√(1−(1/u^6 ))) = let (1/u^6 ) = t∧t→0 lim_(t→0) (((((1−t)^2 ))^(1/3) −(√(1−t)))/t) = lim_(t→0) −(2/3)(1−t)^(−(1/3)) + (1/(2(√(1−t)))) = −(2/3)+(1/2)=−(4/6)+(3/6)=−(1/6)

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{3}}]{\mathrm{9}^{{x}} \left(\mathrm{3}^{{x}} +\mathrm{1}\right)}−\sqrt{\mathrm{3}^{{x}} \left(\mathrm{3}^{{x}} +\mathrm{1}\right)} \\ $$$${let}\:\mathrm{3}^{{x}} +\mathrm{1}\:=\:{u}^{\mathrm{6}} \:\Rightarrow\mathrm{3}^{{x}} ={u}^{\mathrm{6}} −\mathrm{1} \\ $$$$\:\underset{{u}\rightarrow\infty} {\mathrm{lim}}\:\sqrt[{\mathrm{3}}]{\left(\mathrm{3}^{{x}} \right)^{\mathrm{2}} }\:{u}^{\mathrm{2}} −\sqrt{\mathrm{3}^{{x}} }\:{u}^{\mathrm{3}} \:= \\ $$$$\underset{{u}\rightarrow\infty} {\mathrm{lim}}{u}^{\mathrm{2}} \:\sqrt[{\mathrm{3}}]{\left({u}^{\mathrm{6}} −\mathrm{1}\right)^{\mathrm{2}} }−{u}^{\mathrm{3}} \:\sqrt{{u}^{\mathrm{6}} −\mathrm{1}}\:= \\ $$$$\underset{{u}\rightarrow\infty} {\mathrm{lim}}\:{u}^{\mathrm{6}} \:\sqrt[{\mathrm{3}}]{\left(\mathrm{1}−\frac{\mathrm{1}}{{u}^{\mathrm{6}} }\right)^{\mathrm{2}} }−{u}^{\mathrm{6}} \:\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{u}^{\mathrm{6}} }}\:= \\ $$$${let}\:\frac{\mathrm{1}}{{u}^{\mathrm{6}} }\:=\:{t}\wedge{t}\rightarrow\mathrm{0} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }−\sqrt{\mathrm{1}−{t}}}{{t}}\:= \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{1}}{\mathrm{3}}} +\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}−{t}}}\:= \\ $$$$−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{4}}{\mathrm{6}}+\frac{\mathrm{3}}{\mathrm{6}}=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Answered by Aras last updated on 06/Sep/21

$$ \\ $$

Answered by bramlexs22 last updated on 07/Sep/21

lim_(x→∞) 3^x (((1+(1/3^x )))^(1/3) −(√(1+(1/3^x )))) = lim_(x→0) ((((+x))^(1/3) −(√(1+x)))/x) = (1/3)−(1/2)=−(1/6)

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}3}^{\mathrm{x}} \left(\sqrt[{\mathrm{3}}]{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }}−\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }}\right) \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{+\mathrm{x}}−\sqrt{\mathrm{1}+\mathrm{x}}}{\mathrm{x}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com