Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 153518 by Tawa11 last updated on 08/Sep/21

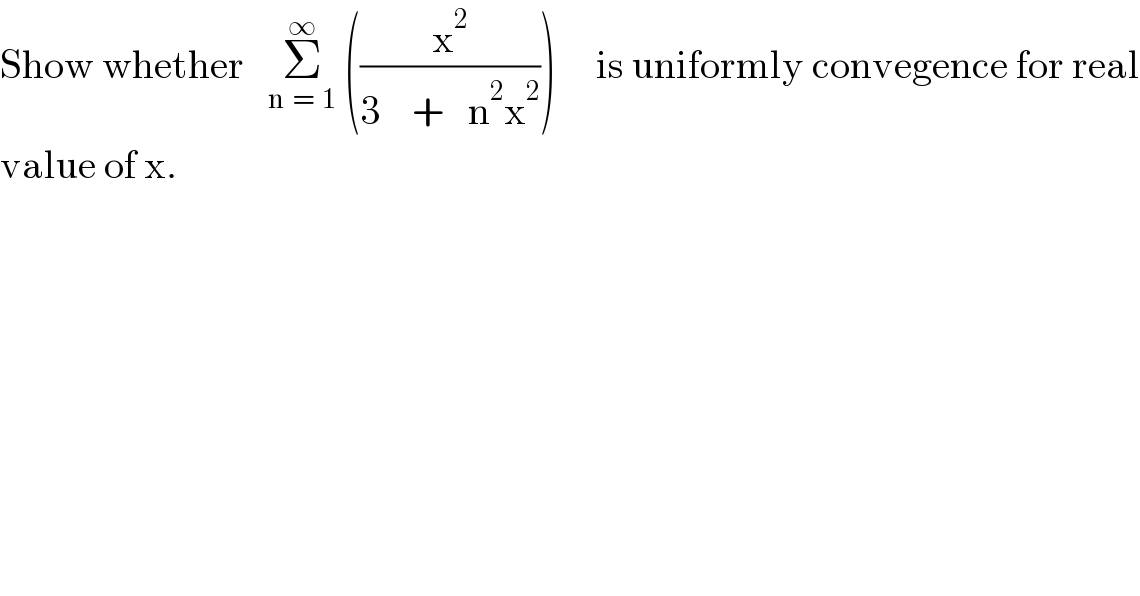
Show whether Σ_(n = 1) ^∞ ((x^2 /(3 + n^2 x^2 ))) is uniformly convegence for real value of x.

$$\mathrm{Show}\:\mathrm{whether}\:\:\:\underset{\mathrm{n}\:\:=\:\:\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}\:\:\:\:+\:\:\:\mathrm{n}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }\right)\:\:\:\:\:\mathrm{is}\:\mathrm{uniformly}\:\mathrm{convegence}\:\mathrm{for}\:\mathrm{real} \\ $$$$\mathrm{value}\:\mathrm{of}\:\mathrm{x}. \\ $$

Answered by puissant last updated on 08/Sep/21

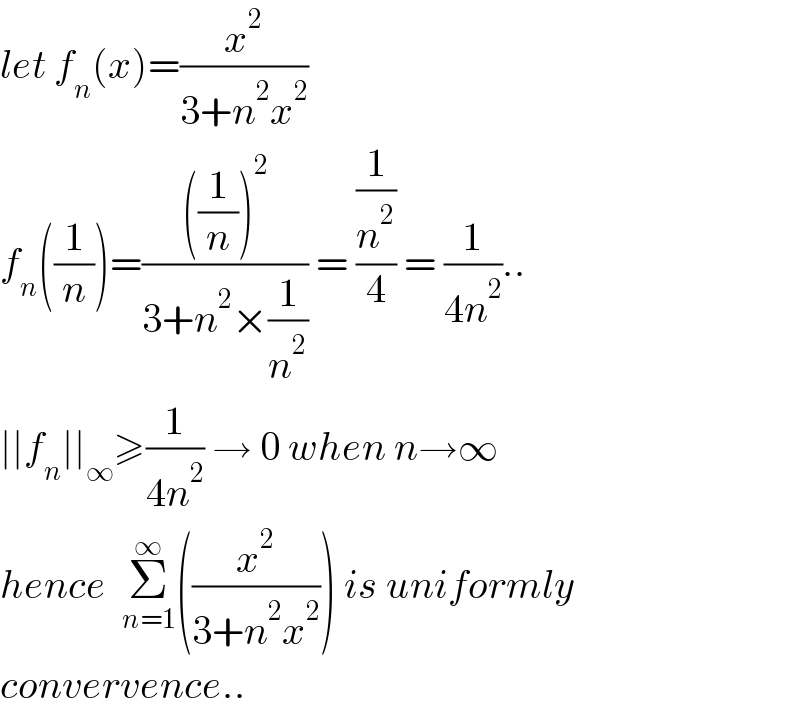
let f_n (x)=(x^2 /(3+n^2 x^2 )) f_n ((1/n))=((((1/n))^2 )/(3+n^2 ×(1/n^2 ))) = ((1/n^2 )/4) = (1/(4n^2 )).. ∣∣f_n ∣∣_∞ ≥(1/(4n^2 )) → 0 when n→∞ hence Σ_(n=1) ^∞ ((x^2 /(3+n^2 x^2 ))) is uniformly convervence..

$${let}\:{f}_{{n}} \left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{3}+{n}^{\mathrm{2}} {x}^{\mathrm{2}} } \\ $$$${f}_{{n}} \left(\frac{\mathrm{1}}{{n}}\right)=\frac{\left(\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} }{\mathrm{3}+{n}^{\mathrm{2}} ×\frac{\mathrm{1}}{{n}^{\mathrm{2}} }}\:=\:\frac{\frac{\mathrm{1}}{{n}^{\mathrm{2}} }}{\mathrm{4}}\:=\:\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }.. \\ $$$$\mid\mid{f}_{{n}} \mid\mid_{\infty} \geqslant\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\:\rightarrow\:\mathrm{0}\:{when}\:{n}\rightarrow\infty \\ $$$${hence}\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{3}+{n}^{\mathrm{2}} {x}^{\mathrm{2}} }\right)\:{is}\:{uniformly}\: \\ $$$${convervence}.. \\ $$

Commented by Tawa11 last updated on 08/Sep/21

God bless you sir. I appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Answered by mindispower last updated on 08/Sep/21

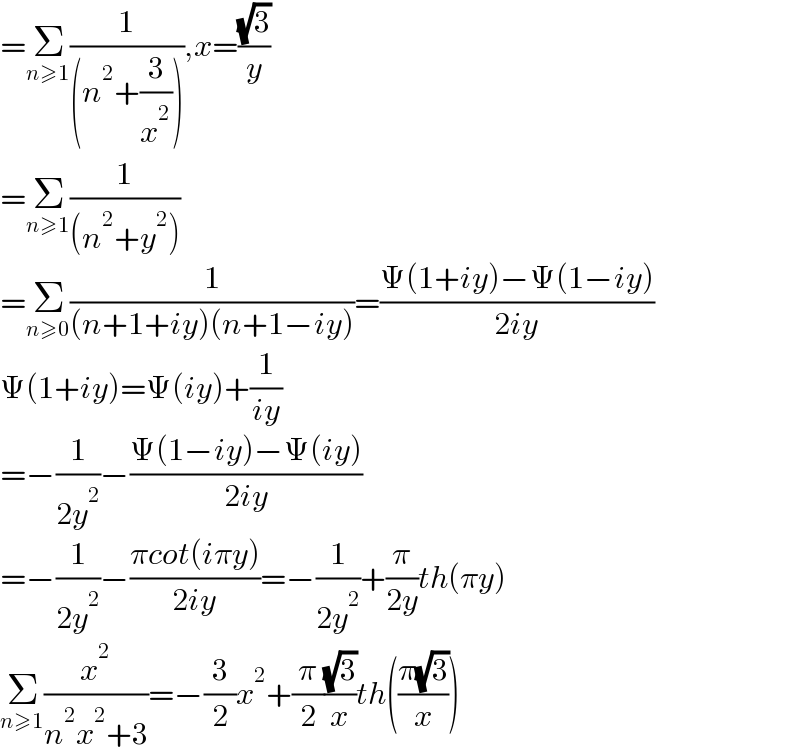
=Σ_(n≥1) (1/((n^2 +(3/x^2 )))),x=((√3)/y) =Σ_(n≥1) (1/((n^2 +y^2 ))) =Σ_(n≥0) (1/((n+1+iy)(n+1−iy)))=((Ψ(1+iy)−Ψ(1−iy))/(2iy)) Ψ(1+iy)=Ψ(iy)+(1/(iy)) =−(1/(2y^2 ))−((Ψ(1−iy)−Ψ(iy))/(2iy)) =−(1/(2y^2 ))−((πcot(iπy))/(2iy))=−(1/(2y^2 ))+(π/(2y))th(πy) Σ_(n≥1) (x^2 /(n^2 x^2 +3))=−(3/2)x^2 +(π/2)((√3)/x)th(((π(√3))/x))

$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +\frac{\mathrm{3}}{{x}^{\mathrm{2}} }\right)},{x}=\frac{\sqrt{\mathrm{3}}}{{y}} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+\mathrm{1}+{iy}\right)\left({n}+\mathrm{1}−{iy}\right)}=\frac{\Psi\left(\mathrm{1}+{iy}\right)−\Psi\left(\mathrm{1}−{iy}\right)}{\mathrm{2}{iy}} \\ $$$$\Psi\left(\mathrm{1}+{iy}\right)=\Psi\left({iy}\right)+\frac{\mathrm{1}}{{iy}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} }−\frac{\Psi\left(\mathrm{1}−{iy}\right)−\Psi\left({iy}\right)}{\mathrm{2}{iy}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} }−\frac{\pi{cot}\left({i}\pi{y}\right)}{\mathrm{2}{iy}}=−\frac{\mathrm{1}}{\mathrm{2}{y}^{\mathrm{2}} }+\frac{\pi}{\mathrm{2}{y}}{th}\left(\pi{y}\right) \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{3}}=−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{\pi}{\mathrm{2}}\frac{\sqrt{\mathrm{3}}}{{x}}{th}\left(\frac{\pi\sqrt{\mathrm{3}}}{{x}}\right) \\ $$

Commented by Tawa11 last updated on 08/Sep/21

God bless you sir. I appreciate.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{appreciate}. \\ $$

Commented by Tawa11 last updated on 08/Sep/21

What is th sir.

$$\mathrm{What}\:\mathrm{is}\:\:\mathrm{th}\:\:\mathrm{sir}. \\ $$

Commented by mindispower last updated on 08/Sep/21

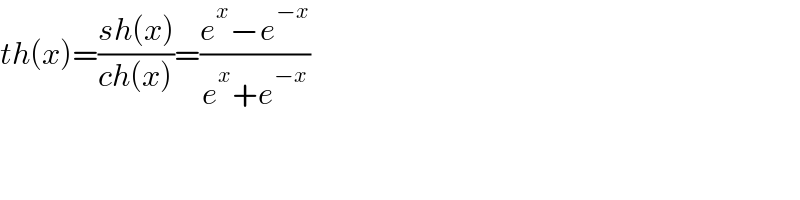
th(x)=((sh(x))/(ch(x)))=((e^x −e^(−x) )/(e^x +e^(−x) ))

$${th}\left({x}\right)=\frac{{sh}\left({x}\right)}{{ch}\left({x}\right)}=\frac{{e}^{{x}} −{e}^{−{x}} }{{e}^{{x}} +{e}^{−{x}} } \\ $$

Commented by Tawa11 last updated on 08/Sep/21

Ohh. Thanks sir

$$\mathrm{Ohh}.\:\mathrm{Thanks}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com