Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 15352 by Tinkutara last updated on 09/Jun/17

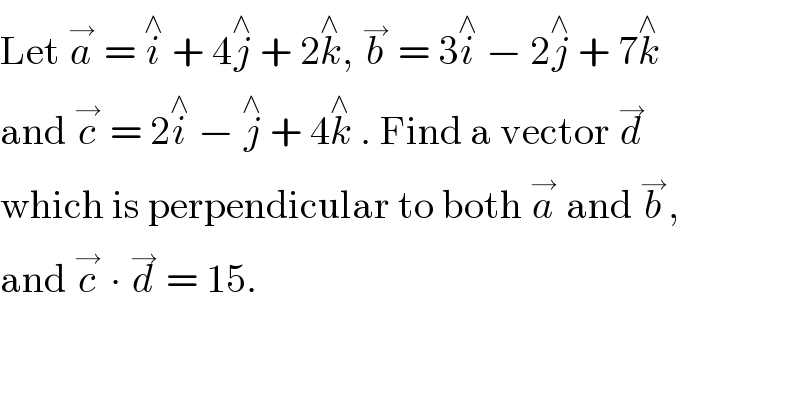
Let a^→ = i^∧ + 4j^∧ + 2k^∧ , b^→ = 3i^∧ − 2j^∧ + 7k^∧ and c^→ = 2i^∧ − j^∧ + 4k^∧ . Find a vector d^→ which is perpendicular to both a^→ and b^→ , and c^→ ∙ d^→ = 15.

$$\mathrm{Let}\:\overset{\rightarrow} {{a}}\:=\:\overset{\wedge} {{i}}\:+\:\mathrm{4}\overset{\wedge} {{j}}\:+\:\mathrm{2}\overset{\wedge} {{k}},\:\overset{\rightarrow} {{b}}\:=\:\mathrm{3}\overset{\wedge} {{i}}\:−\:\mathrm{2}\overset{\wedge} {{j}}\:+\:\mathrm{7}\overset{\wedge} {{k}} \\ $$$$\mathrm{and}\:\overset{\rightarrow} {{c}}\:=\:\mathrm{2}\overset{\wedge} {{i}}\:−\:\overset{\wedge} {{j}}\:+\:\mathrm{4}\overset{\wedge} {{k}}\:.\:\mathrm{Find}\:\mathrm{a}\:\mathrm{vector}\:\overset{\rightarrow} {{d}} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{both}\:\overset{\rightarrow} {{a}}\:\mathrm{and}\:\overset{\rightarrow} {{b}}, \\ $$$$\mathrm{and}\:\overset{\rightarrow} {{c}}\:\centerdot\:\overset{\rightarrow} {{d}}\:=\:\mathrm{15}. \\ $$

Commented by prakash jain last updated on 10/Jun/17

a^→ ×b^→ = determinant ((i,j,k),(1,4,2),(3,(−2),7)) =i(28+4)−j(7−6)+k(−2−12) =32i−j−14k a^→ ×b^→ is perpendicular to both a and b. unit vector perpendicular to a and b n=((a×b)/(∣a×b∣))=((32i−j−14k)/(√(32^2 +1+14^2 )))=((32i−j−14k)/(√(1221))) d=kn=k((32i−j−14k)/(√(1221))) c∙d=15 k((32×2+1−14×4)/(√(1221)))=15 k(9/(√(1221)))=15 k=((15(√(1221)))/9) d=kn=((15(√(1221)))/9)(((32i−j−14k)/(√(1221)))) d=(5/3)(32i−j−14k)

$$\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}=\begin{vmatrix}{\boldsymbol{{i}}}&{\boldsymbol{{j}}}&{\boldsymbol{{k}}}\\{\mathrm{1}}&{\mathrm{4}}&{\mathrm{2}}\\{\mathrm{3}}&{−\mathrm{2}}&{\mathrm{7}}\end{vmatrix} \\ $$$$=\boldsymbol{{i}}\left(\mathrm{28}+\mathrm{4}\right)−\boldsymbol{{j}}\left(\mathrm{7}−\mathrm{6}\right)+\boldsymbol{{k}}\left(−\mathrm{2}−\mathrm{12}\right) \\ $$$$=\mathrm{32}\boldsymbol{{i}}−\boldsymbol{{j}}−\mathrm{14}\boldsymbol{{k}} \\ $$$$\overset{\rightarrow} {{a}}×\overset{\rightarrow} {{b}}\:\mathrm{is}\:\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{both}\:\boldsymbol{{a}}\:\mathrm{and}\:\boldsymbol{{b}}. \\ $$$${unit}\:{vector}\:{perpendicular}\:{to}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}} \\ $$$$\boldsymbol{{n}}=\frac{\boldsymbol{{a}}×\boldsymbol{{b}}}{\mid\boldsymbol{{a}}×\boldsymbol{{b}}\mid}=\frac{\mathrm{32}{i}−{j}−\mathrm{14}{k}}{\sqrt{\mathrm{32}^{\mathrm{2}} +\mathrm{1}+\mathrm{14}^{\mathrm{2}} }}=\frac{\mathrm{32}{i}−{j}−\mathrm{14}{k}}{\sqrt{\mathrm{1221}}} \\ $$$$\boldsymbol{{d}}={k}\boldsymbol{{n}}={k}\frac{\mathrm{32}{i}−{j}−\mathrm{14}{k}}{\sqrt{\mathrm{1221}}} \\ $$$$\boldsymbol{{c}}\centerdot\boldsymbol{{d}}=\mathrm{15} \\ $$$${k}\frac{\mathrm{32}×\mathrm{2}+\mathrm{1}−\mathrm{14}×\mathrm{4}}{\sqrt{\mathrm{1221}}}=\mathrm{15} \\ $$$${k}\frac{\mathrm{9}}{\sqrt{\mathrm{1221}}}=\mathrm{15} \\ $$$${k}=\frac{\mathrm{15}\sqrt{\mathrm{1221}}}{\mathrm{9}} \\ $$$$\boldsymbol{{d}}={k}\boldsymbol{{n}}=\frac{\mathrm{15}\sqrt{\mathrm{1221}}}{\mathrm{9}}\left(\frac{\mathrm{32}\boldsymbol{{i}}−\boldsymbol{{j}}−\mathrm{14}\boldsymbol{{k}}}{\sqrt{\mathrm{1221}}}\right) \\ $$$$\boldsymbol{{d}}=\frac{\mathrm{5}}{\mathrm{3}}\left(\mathrm{32}\boldsymbol{{i}}−\boldsymbol{{j}}−\mathrm{14}\boldsymbol{{k}}\right) \\ $$

Commented by Tinkutara last updated on 10/Jun/17

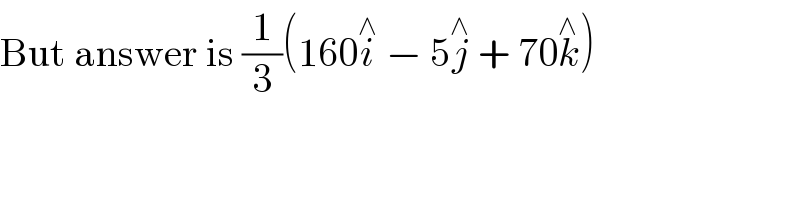
But answer is (1/3)(160i^∧ − 5j^∧ + 70k^∧ )

$$\mathrm{But}\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{160}\overset{\wedge} {{i}}\:−\:\mathrm{5}\overset{\wedge} {{j}}\:+\:\mathrm{70}\overset{\wedge} {{k}}\right) \\ $$

Commented by prakash jain last updated on 10/Jun/17

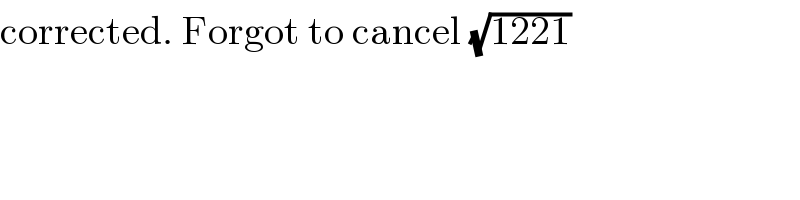
corrected. Forgot to cancel (√(1221))

$$\mathrm{corrected}.\:\mathrm{Forgot}\:\mathrm{to}\:\mathrm{cancel}\:\sqrt{\mathrm{1221}} \\ $$

Commented by Tinkutara last updated on 10/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com