Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 15358 by Tinkutara last updated on 09/Jun/17

If a^→ , b^→ , c^→ are mutually perpendicular vectors of equal magnitudes, show that the vector a^→ + b^→ + c^→ is equally inclined to a^→ , b^→ and c^→ .

$$\mathrm{If}\:\overset{\rightarrow} {{a}},\:\overset{\rightarrow} {{b}},\:\overset{\rightarrow} {{c}}\:\mathrm{are}\:\mathrm{mutually}\:\mathrm{perpendicular} \\ $$$$\mathrm{vectors}\:\mathrm{of}\:\mathrm{equal}\:\mathrm{magnitudes},\:\mathrm{show}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{vector}\:\overset{\rightarrow} {{a}}\:+\:\overset{\rightarrow} {{b}}\:+\:\overset{\rightarrow} {{c}}\:\mathrm{is}\:\mathrm{equally}\:\mathrm{inclined} \\ $$$$\mathrm{to}\:\overset{\rightarrow} {{a}},\:\overset{\rightarrow} {{b}}\:\mathrm{and}\:\overset{\rightarrow} {{c}}\:. \\ $$

Answered by prakash jain last updated on 09/Jun/17

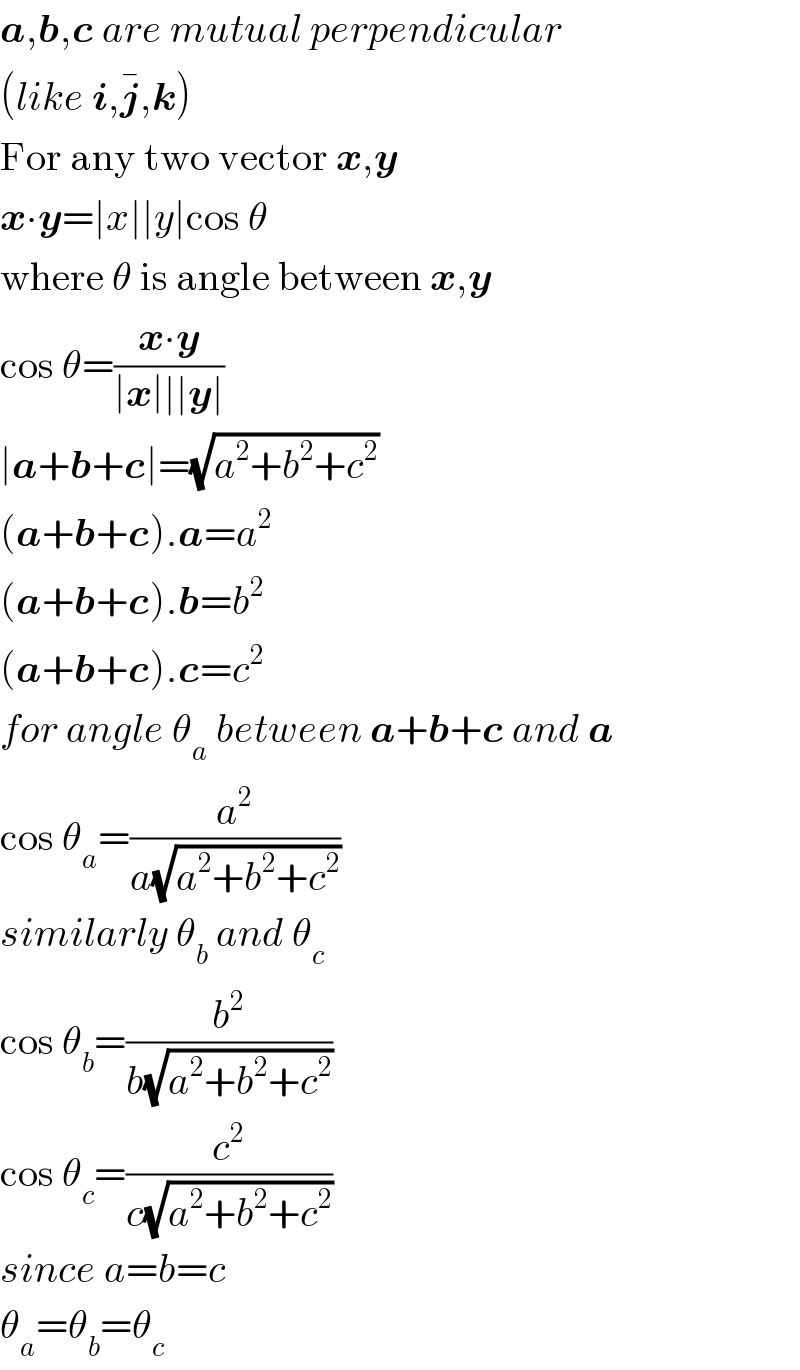
a,b,c are mutual perpendicular (like i,j^� ,k) For any two vector x,y x∙y=∣x∣∣y∣cos θ where θ is angle between x,y cos θ=((x∙y)/(∣x∣∣∣y∣)) ∣a+b+c∣=(√(a^2 +b^2 +c^2 )) (a+b+c).a=a^2 (a+b+c).b=b^2 (a+b+c).c=c^2 for angle θ_a between a+b+c and a cos θ_a =(a^2 /(a(√(a^2 +b^2 +c^2 )))) similarly θ_b and θ_c cos θ_b =(b^2 /(b(√(a^2 +b^2 +c^2 )))) cos θ_c =(c^2 /(c(√(a^2 +b^2 +c^2 )))) since a=b=c θ_a =θ_b =θ_c

$$\boldsymbol{{a}},\boldsymbol{{b}},\boldsymbol{{c}}\:{are}\:{mutual}\:{perpendicular} \\ $$$$\left({like}\:\boldsymbol{{i}},\bar {\boldsymbol{{j}}},\boldsymbol{{k}}\right) \\ $$$$\mathrm{For}\:\mathrm{any}\:\mathrm{two}\:\mathrm{vector}\:\boldsymbol{{x}},\boldsymbol{{y}} \\ $$$$\boldsymbol{{x}}\centerdot\boldsymbol{{y}}=\mid{x}\mid\mid{y}\mid\mathrm{cos}\:\theta \\ $$$$\mathrm{where}\:\theta\:\mathrm{is}\:\mathrm{angle}\:\mathrm{between}\:\boldsymbol{{x}},\boldsymbol{{y}} \\ $$$$\mathrm{cos}\:\theta=\frac{\boldsymbol{{x}}\centerdot\boldsymbol{{y}}}{\mid\boldsymbol{{x}}\mid\mid\mid\boldsymbol{{y}}\mid} \\ $$$$\mid\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right).\boldsymbol{{a}}={a}^{\mathrm{2}} \\ $$$$\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right).\boldsymbol{{b}}={b}^{\mathrm{2}} \\ $$$$\left(\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\right).\boldsymbol{{c}}={c}^{\mathrm{2}} \\ $$$${for}\:{angle}\:\theta_{{a}} \:{between}\:\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\:{and}\:\boldsymbol{{a}} \\ $$$$\mathrm{cos}\:\theta_{{a}} =\frac{{a}^{\mathrm{2}} }{{a}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$${similarly}\:\theta_{{b}} \:{and}\:\theta_{{c}} \\ $$$$\mathrm{cos}\:\theta_{{b}} =\frac{{b}^{\mathrm{2}} }{{b}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$$\mathrm{cos}\:\theta_{{c}} =\frac{{c}^{\mathrm{2}} }{{c}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }} \\ $$$${since}\:{a}={b}={c} \\ $$$$\theta_{{a}} =\theta_{{b}} =\theta_{{c}} \\ $$

Commented by Tinkutara last updated on 10/Jun/17

Thanks Sir!

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com