
Question and Answers Forum
Question Number 1540 by Rasheed Soomro last updated on 17/Aug/15
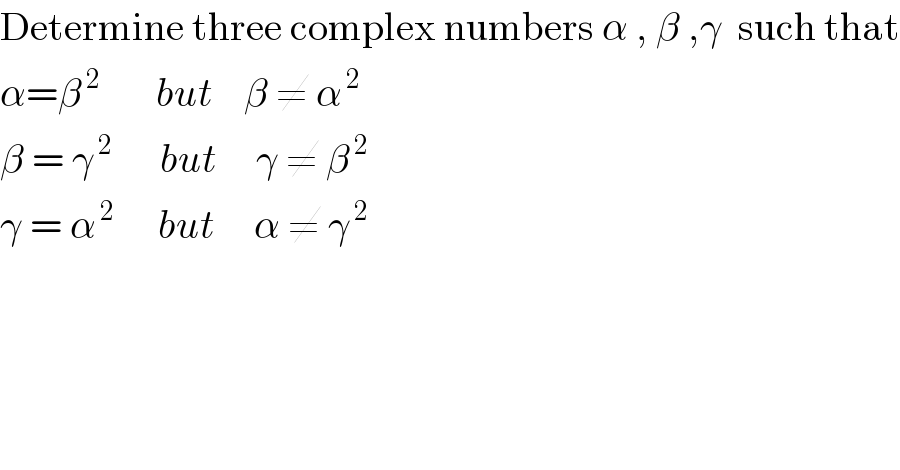
Answered by 123456 last updated on 17/Aug/15
![{ ((α=β^2 ∧β≠α^2 )),((β=γ^2 ∧γ≠β^2 )),((γ=α^2 ∧α≠γ^2 )) :}≡ { ((α=β^2 ∧β≠γ)),((β=γ^2 ∧γ≠α)),((γ=α^2 ∧α≠β)) :} α=β^2 =(γ^2 )^2 =[(α^2 )^2 ]^2 =α^(2×2×2) =α^8 α^8 −α=0 α(α^7 −1)=0 α=0∨α^7 =1 α=0⇒γ=0⇒γ^2 =α α=e^(((2π)/7)kı) ,k∈Z_7 γ=α^2 =e^(((4π)/7)kı) β=γ^2 =e^(((8π)/7)kı) (α,β,γ)=(e^(((2π)/7)kı) ,e^(((8π)/7)kı) ,e^(((4π)/7)kι) ) β≠α^2 ⇒e^(((8π)/7)kı) ≠e^(((4π)/7)kı) (k≠0) γ≠β^2 ⇒e^(((4π)/7)kı) ≠e^(((16π)/7)kı) =e^(((2π)/7)kı) (k≠0) α≠γ^2 ⇒e^(((2π)/7)kı) ≠e^(((8π)/7)kı) (k≠0) (α,β,γ)=(e^(((2π)/7)kı) ,e^(((8π)/7)kı) ,e^(((4π)/7)kı) ),k∈Z_7 \{0}](Q1541.png)
Commented by 123456 last updated on 17/Aug/15

| ||
Question and Answers Forum | ||
Question Number 1540 by Rasheed Soomro last updated on 17/Aug/15 | ||
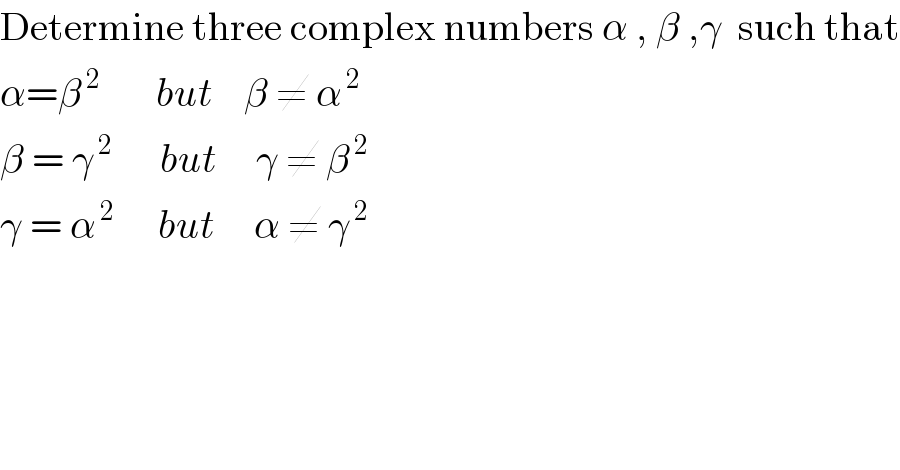 | ||
Answered by 123456 last updated on 17/Aug/15 | ||
![{ ((α=β^2 ∧β≠α^2 )),((β=γ^2 ∧γ≠β^2 )),((γ=α^2 ∧α≠γ^2 )) :}≡ { ((α=β^2 ∧β≠γ)),((β=γ^2 ∧γ≠α)),((γ=α^2 ∧α≠β)) :} α=β^2 =(γ^2 )^2 =[(α^2 )^2 ]^2 =α^(2×2×2) =α^8 α^8 −α=0 α(α^7 −1)=0 α=0∨α^7 =1 α=0⇒γ=0⇒γ^2 =α α=e^(((2π)/7)kı) ,k∈Z_7 γ=α^2 =e^(((4π)/7)kı) β=γ^2 =e^(((8π)/7)kı) (α,β,γ)=(e^(((2π)/7)kı) ,e^(((8π)/7)kı) ,e^(((4π)/7)kι) ) β≠α^2 ⇒e^(((8π)/7)kı) ≠e^(((4π)/7)kı) (k≠0) γ≠β^2 ⇒e^(((4π)/7)kı) ≠e^(((16π)/7)kı) =e^(((2π)/7)kı) (k≠0) α≠γ^2 ⇒e^(((2π)/7)kı) ≠e^(((8π)/7)kı) (k≠0) (α,β,γ)=(e^(((2π)/7)kı) ,e^(((8π)/7)kı) ,e^(((4π)/7)kı) ),k∈Z_7 \{0}](Q1541.png) | ||
| ||
Commented by 123456 last updated on 17/Aug/15 | ||
 | ||