
Question Number 154103 by SANOGO last updated on 14/Sep/21
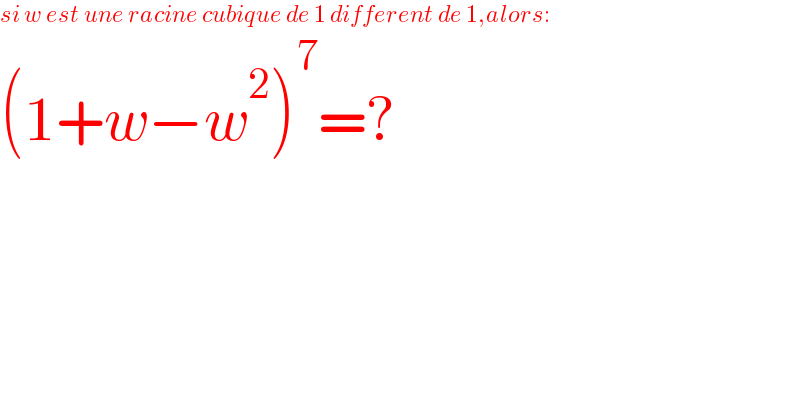
$${si}\:{w}\:{est}\:{une}\:{racine}\:{cubique}\:{de}\:\mathrm{1}\:{different}\:{de}\:\mathrm{1},{alors}: \\ $$$$\left(\mathrm{1}+{w}−{w}^{\mathrm{2}} \right)^{\mathrm{7}} =? \\ $$
Commented by ZiYangLee last updated on 14/Sep/21
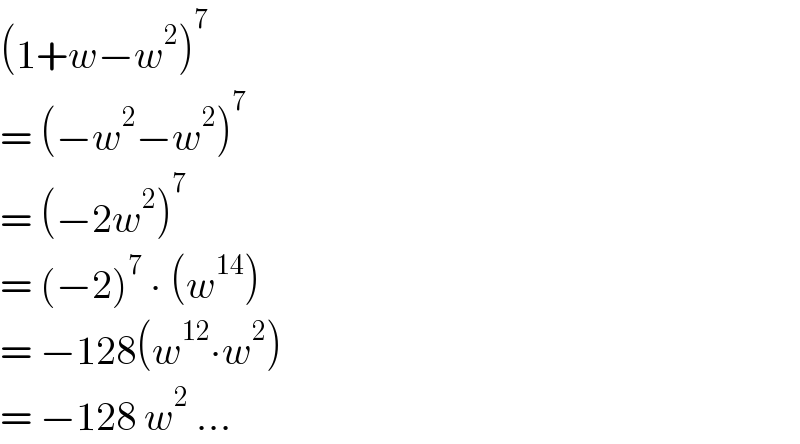
$$\left(\mathrm{1}+{w}−{w}^{\mathrm{2}} \right)^{\mathrm{7}} \\ $$$$=\:\left(−{w}^{\mathrm{2}} −{w}^{\mathrm{2}} \right)^{\mathrm{7}} \\ $$$$=\:\left(−\mathrm{2}{w}^{\mathrm{2}} \right)^{\mathrm{7}} \\ $$$$=\:\left(−\mathrm{2}\right)^{\mathrm{7}} \:\centerdot\:\left({w}^{\mathrm{14}} \right) \\ $$$$=\:−\mathrm{128}\left({w}^{\mathrm{12}} \centerdot{w}^{\mathrm{2}} \right) \\ $$$$=\:−\mathrm{128}\:{w}^{\mathrm{2}} \:... \\ $$
Commented by SANOGO last updated on 14/Sep/21
$${merc}\:{bien} \\ $$
Answered by Jonathanwaweh last updated on 14/Sep/21

$$ \\ $$puisque w est une racine cubique différent de 1 alors 1+w+w^2=0 donc 1+w=-w^2 il vient que (1+w-w^2)^7=(-w^2-w^2)^7=-2^7(w)^14 or 14=3*4+2 donc w^14=(w^3)^4*w^2=1*w^2 finalement on a (1+w-w^2)^7=-(2^7)(w^2)
Commented by SANOGO last updated on 17/Sep/21
$${merci}\:{bien}\:{le}\:{grand} \\ $$
Answered by puissant last updated on 14/Sep/21
![posons w=e^(i((2π)/3)) =−(1/2)+((√3)/2)i et w^2 =e^(i((4π)/3)) =e^(−i((2π)/3)) =−(1/2)−((√3)/2)i alors (1+w−w)=(1−(1/2)+((√3)/2)i+(1/2)+((√3)/2)i)=(1+(√3)i) alors , (1+w−w^2 )^7 =(1+i(√3))^7 = [2((1/2)+i((√3)/2))]^7 =2^7 (e^(i(π/3)) )^7 = 128 e^(i((7π)/3)) ∴∵ (1+w−w^2 )^7 = 128 e^((iπ)/3) =128(√w)..(car ((7π)/3)≡(π/3)[2π])..](Q154111.png)
$${posons}\:{w}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} =−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i} \\ $$$${et}\:{w}^{\mathrm{2}} ={e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} ={e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} =−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i} \\ $$$${alors}\:\left(\mathrm{1}+{w}−{w}\right)=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right)=\left(\mathrm{1}+\sqrt{\mathrm{3}}{i}\right) \\ $$$${alors}\:, \\ $$$$\:\left(\mathrm{1}+{w}−{w}^{\mathrm{2}} \right)^{\mathrm{7}} =\left(\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)^{\mathrm{7}} =\:\left[\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right]^{\mathrm{7}} \\ $$$$=\mathrm{2}^{\mathrm{7}} \left({e}^{{i}\frac{\pi}{\mathrm{3}}} \right)^{\mathrm{7}} =\:\mathrm{128}\:{e}^{{i}\frac{\mathrm{7}\pi}{\mathrm{3}}} \\ $$$$ \\ $$$$\therefore\because\:\:\left(\mathrm{1}+{w}−{w}^{\mathrm{2}} \right)^{\mathrm{7}} =\:\mathrm{128}\:{e}^{\frac{{i}\pi}{\mathrm{3}}} =\mathrm{128}\sqrt{{w}}..\left({car}\:\frac{\mathrm{7}\pi}{\mathrm{3}}\equiv\frac{\pi}{\mathrm{3}}\left[\mathrm{2}\pi\right]\right).. \\ $$$$ \\ $$
Commented by SANOGO last updated on 14/Sep/21
$${merci}\:{bien} \\ $$
