Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 154143 by mnjuly1970 last updated on 14/Sep/21

Answered by phanphuoc last updated on 14/Sep/21

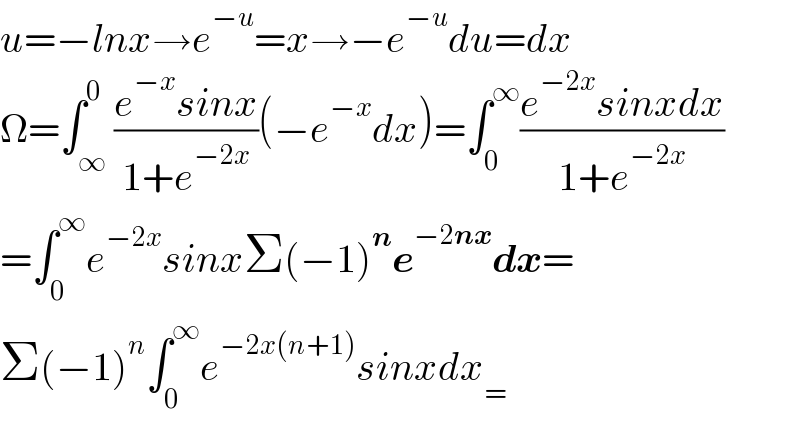
u=−lnx→e^(−u) =x→−e^(−u) du=dx Ω=∫_∞ ^0 ((e^(−x) sinx)/(1+e^(−2x) ))(−e^(−x) dx)=∫_0 ^∞ ((e^(−2x) sinxdx)/(1+e^(−2x) )) =∫_0 ^∞ e^(−2x) sinxΣ(−1)^n e^(−2nx) dx= Σ(−1)^n ∫_0 ^∞ e^(−2x(n+1)) sinxdx_=

$${u}=−{lnx}\rightarrow{e}^{−{u}} ={x}\rightarrow−{e}^{−{u}} {du}={dx} \\ $$$$\Omega=\int_{\infty} ^{\mathrm{0}} \frac{{e}^{−{x}} {sinx}}{\mathrm{1}+{e}^{−\mathrm{2}{x}} }\left(−{e}^{−{x}} {dx}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\mathrm{2}{x}} {sinxdx}}{\mathrm{1}+{e}^{−\mathrm{2}{x}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}} {sinx}\Sigma\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} \boldsymbol{{e}}^{−\mathrm{2}\boldsymbol{{nx}}} \boldsymbol{{dx}}= \\ $$$$\Sigma\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{x}\left({n}+\mathrm{1}\right)} {sinxdx}_{=} \\ $$

Answered by puissant last updated on 14/Sep/21

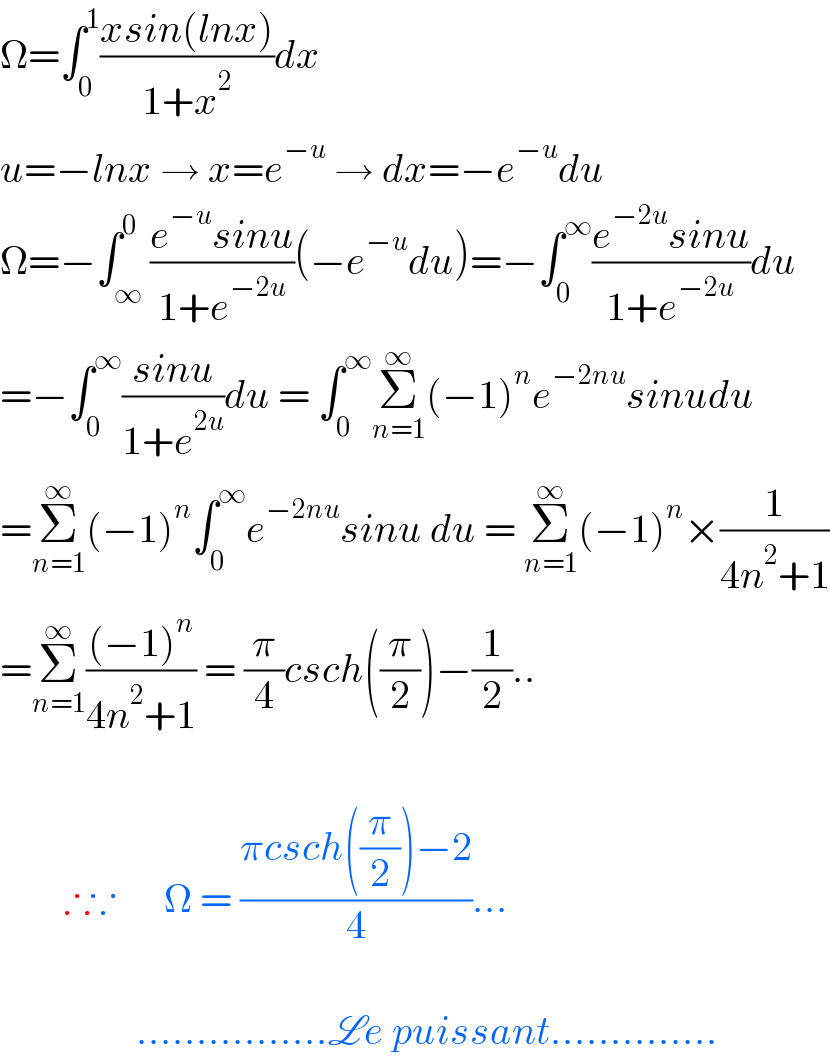
Ω=∫_0 ^1 ((xsin(lnx))/(1+x^2 ))dx u=−lnx → x=e^(−u) → dx=−e^(−u) du Ω=−∫_∞ ^0 ((e^(−u) sinu)/(1+e^(−2u) ))(−e^(−u) du)=−∫_0 ^∞ ((e^(−2u) sinu)/(1+e^(−2u) ))du =−∫_0 ^∞ ((sinu)/(1+e^(2u) ))du = ∫_0 ^∞ Σ_(n=1) ^∞ (−1)^n e^(−2nu) sinudu =Σ_(n=1) ^∞ (−1)^n ∫_0 ^∞ e^(−2nu) sinu du = Σ_(n=1) ^∞ (−1)^n ×(1/(4n^2 +1)) =Σ_(n=1) ^∞ (((−1)^n )/(4n^2 +1)) = (π/4)csch((π/2))−(1/2).. ∴∵ Ω = ((πcsch((π/2))−2)/4)... ................Le puissant..............

$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{xsin}\left({lnx}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${u}=−{lnx}\:\rightarrow\:{x}={e}^{−{u}} \:\rightarrow\:{dx}=−{e}^{−{u}} {du} \\ $$$$\Omega=−\int_{\infty} ^{\mathrm{0}} \frac{{e}^{−{u}} {sinu}}{\mathrm{1}+{e}^{−\mathrm{2}{u}} }\left(−{e}^{−{u}} {du}\right)=−\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\mathrm{2}{u}} {sinu}}{\mathrm{1}+{e}^{−\mathrm{2}{u}} }{du} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \frac{{sinu}}{\mathrm{1}+{e}^{\mathrm{2}{u}} }{du}\:=\:\int_{\mathrm{0}} ^{\infty} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {e}^{−\mathrm{2}{nu}} {sinudu} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{nu}} {sinu}\:{du}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} ×\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}\:=\:\frac{\pi}{\mathrm{4}}{csch}\left(\frac{\pi}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\therefore\because\:\:\:\:\:\:\Omega\:=\:\frac{\pi{csch}\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{2}}{\mathrm{4}}... \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:................\mathscr{L}{e}\:{puissant}.............. \\ $$

Commented by mnjuly1970 last updated on 15/Sep/21

grate..

$${grate}.. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com