Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 1543 by 112358 last updated on 17/Aug/15

Let a, b∈R. Show that ∣∣a∣−∣b∣∣≤∣a−b∣.

$${Let}\:{a},\:{b}\in\mathbb{R}.\:{Show}\:{that}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mid{a}\mid−\mid{b}\mid\mid\leqslant\mid{a}−{b}\mid. \\ $$

Answered by Rasheed Soomro last updated on 18/Aug/15

Alternative way , technically simpler. ∣∣a∣−∣b∣∣≤∣a−b∣......................(I) Let ∣a∣ = x and ∣b∣ = y , Clearly x,y≥0 ∣a∣=x ⇒ a=±x and ∣b∣=±y By substituting in (I) we have four simpler inequalities: ∣ x−y ∣≤ ∣ (+x)−(+y) ∣= ∣ x−y ∣......................(II) ≤ ∣ (+x)−(−y) ∣=∣ x+y ∣.......(III) ≤∣ (−x)−(+y) ∣=∣−(x+y)∣= ∣ x+y ∣..........(IV) ≤∣ (−x)−(−y) ∣=∣ −(x−y) ∣= ∣ x−y ∣ .....(V) (II) and (V) are obvious.For (III) and (IV) we proceed as follow x−y≤x+y for x and y are both +ve. ∴ ∣ x−y ∣ ≤ ∣x + y∣ Since (II) , (III) , (IV) and (V) are true. It implies that ∣∣a∣−∣b∣∣≤∣a−b∣

$$\boldsymbol{\mathrm{Alternative}}\:\boldsymbol{\mathrm{way}}\:,\:\boldsymbol{\mathrm{technically}}\:\boldsymbol{\mathrm{simpler}}. \\ $$$$\mid\mid{a}\mid−\mid{b}\mid\mid\leqslant\mid{a}−{b}\mid......................\left(\boldsymbol{\mathrm{I}}\right) \\ $$$$\mathrm{L}{et}\:\mid{a}\mid\:=\:{x}\:\:\:\:{and}\:\:\:\:\:\:\mid{b}\mid\:=\:{y}\:\:\:,\:\:{Clearly}\:\:{x},{y}\geqslant\mathrm{0} \\ $$$$\mid{a}\mid={x}\:\Rightarrow\:{a}=\pm{x}\:\:\:{and}\:\:\:\:\:\mid{b}\mid=\pm{y} \\ $$$${By}\:{substituting}\:{in}\:\left(\boldsymbol{\mathrm{I}}\right)\:{we}\:{have}\:{four}\:{simpler}\:\:{inequalities}: \\ $$$$\:\:\:\:\:\:\:\:\:\mid\:{x}−{y}\:\mid\leqslant\:\mid\:\left(+{x}\right)−\left(+{y}\right)\:\mid=\:\mid\:{x}−{y}\:\mid......................\left(\boldsymbol{\mathrm{II}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\leqslant\:\mid\:\left(+{x}\right)−\left(−{y}\right)\:\mid=\mid\:{x}+{y}\:\mid.......\left(\boldsymbol{\mathrm{III}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\leqslant\mid\:\left(−{x}\right)−\left(+{y}\right)\:\mid=\mid−\left({x}+{y}\right)\mid=\:\mid\:{x}+{y}\:\mid..........\left(\boldsymbol{\mathrm{IV}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\leqslant\mid\:\left(−{x}\right)−\left(−{y}\right)\:\mid=\mid\:−\left({x}−{y}\right)\:\mid=\:\mid\:{x}−{y}\:\mid\:.....\left(\boldsymbol{\mathrm{V}}\right) \\ $$$$\left(\boldsymbol{\mathrm{II}}\right)\:\:\:{and}\:\:\left(\boldsymbol{\mathrm{V}}\right)\:\:\:\:{are}\:{obvious}.{For}\:\left(\boldsymbol{\mathrm{III}}\right)\:{and}\:\left(\boldsymbol{\mathrm{IV}}\right)\:{we} \\ $$$${proceed}\:{as}\:{follow} \\ $$$$\:\:\:\:\:\:\:\:\:{x}−{y}\leqslant{x}+{y}\:\:\:{for}\:{x}\:{and}\:{y}\:{are}\:{both}\:+{ve}. \\ $$$$\:\:\:\therefore\:\:\mid\:{x}−{y}\:\mid\:\leqslant\:\mid{x}\:+\:{y}\mid \\ $$$${Since}\:\left(\boldsymbol{\mathrm{II}}\right)\:,\:\:\left(\boldsymbol{\mathrm{III}}\right)\:,\:\left(\boldsymbol{\mathrm{IV}}\right)\:{and}\:\left(\boldsymbol{\mathrm{V}}\right)\:{are}\:{true}.\:{It}\:{implies}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\mid{a}\mid−\mid{b}\mid\mid\leqslant\mid{a}−{b}\mid \\ $$

Answered by 123456 last updated on 17/Aug/15

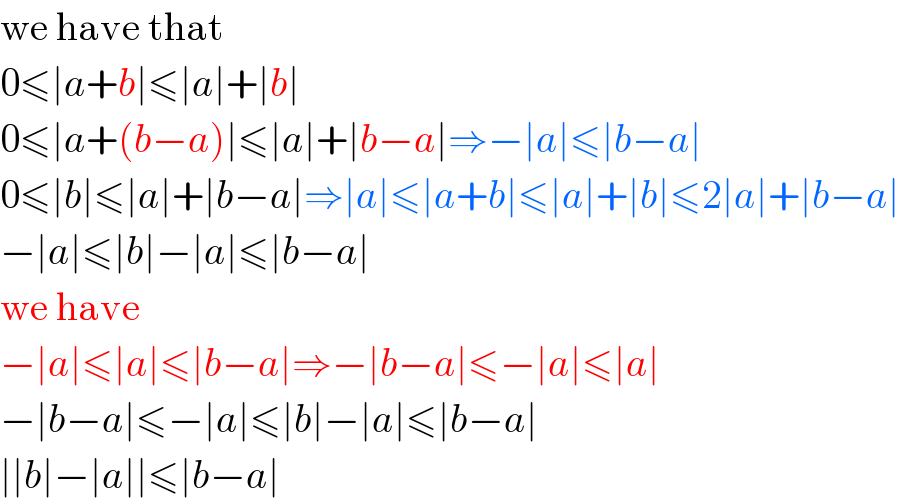
we have that 0≤∣a+b∣≤∣a∣+∣b∣ 0≤∣a+(b−a)∣≤∣a∣+∣b−a∣⇒−∣a∣≤∣b−a∣ 0≤∣b∣≤∣a∣+∣b−a∣⇒∣a∣≤∣a+b∣≤∣a∣+∣b∣≤2∣a∣+∣b−a∣ −∣a∣≤∣b∣−∣a∣≤∣b−a∣ we have −∣a∣≤∣a∣≤∣b−a∣⇒−∣b−a∣≤−∣a∣≤∣a∣ −∣b−a∣≤−∣a∣≤∣b∣−∣a∣≤∣b−a∣ ∣∣b∣−∣a∣∣≤∣b−a∣

$$\mathrm{we}\:\mathrm{have}\:\mathrm{that} \\ $$$$\mathrm{0}\leqslant\mid{a}+{b}\mid\leqslant\mid{a}\mid+\mid{b}\mid \\ $$$$\mathrm{0}\leqslant\mid{a}+\left({b}−{a}\right)\mid\leqslant\mid{a}\mid+\mid{b}−{a}\mid\Rightarrow−\mid{a}\mid\leqslant\mid{b}−{a}\mid \\ $$$$\mathrm{0}\leqslant\mid{b}\mid\leqslant\mid{a}\mid+\mid{b}−{a}\mid\Rightarrow\mid{a}\mid\leqslant\mid{a}+{b}\mid\leqslant\mid{a}\mid+\mid{b}\mid\leqslant\mathrm{2}\mid{a}\mid+\mid{b}−{a}\mid \\ $$$$−\mid{a}\mid\leqslant\mid{b}\mid−\mid{a}\mid\leqslant\mid{b}−{a}\mid \\ $$$$\mathrm{we}\:\mathrm{have} \\ $$$$−\mid{a}\mid\leqslant\mid{a}\mid\leqslant\mid{b}−{a}\mid\Rightarrow−\mid{b}−{a}\mid\leqslant−\mid{a}\mid\leqslant\mid{a}\mid \\ $$$$−\mid{b}−{a}\mid\leqslant−\mid{a}\mid\leqslant\mid{b}\mid−\mid{a}\mid\leqslant\mid{b}−{a}\mid \\ $$$$\mid\mid{b}\mid−\mid{a}\mid\mid\leqslant\mid{b}−{a}\mid \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com