Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 15440 by mrW1 last updated on 10/Jun/17

Commented by mrW1 last updated on 10/Jun/17

The sides of a convex quadrilateral ABCD are elongated 2 times in one direction, see diagram, to form a new quadrilateral EFGH. What is the area of the new quadrilateral if the area of ABCD is 1. What is the result, if the sides will be elongated n times?

$$\mathrm{The}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{a}\:\mathrm{convex}\:\mathrm{quadrilateral} \\ $$$$\mathrm{ABCD}\:\mathrm{are}\:\mathrm{elongated}\:\mathrm{2}\:\mathrm{times}\:\mathrm{in}\:\mathrm{one} \\ $$$$\mathrm{direction},\:\mathrm{see}\:\mathrm{diagram},\:\mathrm{to}\:\mathrm{form}\:\mathrm{a}\:\mathrm{new} \\ $$$$\mathrm{quadrilateral}\:\mathrm{EFGH}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{new}\:\mathrm{quadrilateral}\:\mathrm{if}\:\mathrm{the} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{ABCD}\:\mathrm{is}\:\mathrm{1}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{result},\:\mathrm{if}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{will}\:\mathrm{be} \\ $$$$\mathrm{elongated}\:\mathrm{n}\:\mathrm{times}? \\ $$

Commented by ajfour last updated on 10/Jun/17

n^2 +n+1 is it correct sir ?

$${n}^{\mathrm{2}} +{n}+\mathrm{1} \\ $$$${is}\:{it}\:{correct}\:{sir}\:? \\ $$

Commented by mrW1 last updated on 10/Jun/17

no, this is not correct.

$$\mathrm{no},\:\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}. \\ $$

Commented by ajfour last updated on 10/Jun/17

Commented by ajfour last updated on 10/Jun/17

Expression for Area of original quadrilateral: let area of original quadrilateral be A_0 . Then 2A_0 =(1/2)(absin β+bcsin γ+cdsin δ +dasin α ) ⇒ 2A_0 =(1/2)Σabsin β or Σabsin β=4A_0 . This is used in next figure wberein the solution is continued...

$${Expression}\:{for}\:{Area}\:{of}\:{original} \\ $$$${quadrilateral}: \\ $$$${let}\:{area}\:{of}\:{original}\:{quadrilateral} \\ $$$${be}\:{A}_{\mathrm{0}} .\:{Then} \\ $$$$\mathrm{2}{A}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\left({ab}\mathrm{sin}\:\beta+{bc}\mathrm{sin}\:\gamma+{cd}\mathrm{sin}\:\delta\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{da}\mathrm{sin}\:\alpha\:\right) \\ $$$$\Rightarrow\:\mathrm{2}{A}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\Sigma{ab}\mathrm{sin}\:\beta\: \\ $$$${or}\:\:\:\Sigma{ab}\mathrm{sin}\:\beta=\mathrm{4}{A}_{\mathrm{0}} \:. \\ $$$$\:\:\:\:{This}\:{is}\:{used}\:{in}\:{next}\:{figure} \\ $$$${wberein}\:{the}\:{solution}\:{is}\:{continued}... \\ $$

Commented by ajfour last updated on 10/Jun/17

Commented by ajfour last updated on 10/Jun/17

let area of new quadrilateral be S. S=A_0 +(1/2)[ na(n+1)bsin β +nb(n+1)csin γ +nc(n+1)dsin δ +nd(n+1)asin α ] ⇒ S=A_0 +((n(n+1))/2) Σabsin β it has been found in previous comment that Σabsin β=4A_0 , therefore S=A_0 +((n(n+1))/2)(4A_0 ) S=A_0 (1+2n^2 +2n) or (S/A_0 ) =2n^2 +2n+1 .

$${let}\:{area}\:{of}\:{new}\:{quadrilateral} \\ $$$${be}\:{S}. \\ $$$$\:{S}={A}_{\mathrm{0}} +\frac{\mathrm{1}}{\mathrm{2}}\left[\:{na}\left({n}+\mathrm{1}\right){b}\mathrm{sin}\:\beta\right. \\ $$$$\:\:\:\:\:\:\:\:\:+{nb}\left({n}+\mathrm{1}\right){c}\mathrm{sin}\:\gamma \\ $$$$\:\:\:\:\:\:\:\:\:\:+{nc}\left({n}+\mathrm{1}\right){d}\mathrm{sin}\:\delta \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:+{nd}\left({n}+\mathrm{1}\right){a}\mathrm{sin}\:\alpha\:\right] \\ $$$$\Rightarrow\:{S}={A}_{\mathrm{0}} +\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:\Sigma{ab}\mathrm{sin}\:\beta \\ $$$${it}\:{has}\:{been}\:{found}\:{in}\:{previous} \\ $$$${comment}\:{that}\:\Sigma{ab}\mathrm{sin}\:\beta=\mathrm{4}{A}_{\mathrm{0}} \:, \\ $$$${therefore}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{S}={A}_{\mathrm{0}} +\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\left(\mathrm{4}{A}_{\mathrm{0}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{S}={A}_{\mathrm{0}} \left(\mathrm{1}+\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}\right) \\ $$$$\:\:\:\:{or}\:\:\:\:\frac{{S}}{{A}_{\mathrm{0}} }\:=\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}\:. \\ $$

Commented by mrW1 last updated on 10/Jun/17

Answer 2n^2 +2n+1 is correct!

$$\mathrm{Answer}\:\mathrm{2n}^{\mathrm{2}} +\mathrm{2n}+\mathrm{1}\:\mathrm{is}\:\mathrm{correct}! \\ $$

Commented by ajfour last updated on 10/Jun/17

with n=2 , (S/A_0 ) = 13 .

$${with}\:\:{n}=\mathrm{2}\:,\:\:\frac{{S}}{{A}_{\mathrm{0}} }\:=\:\mathrm{13}\:. \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17

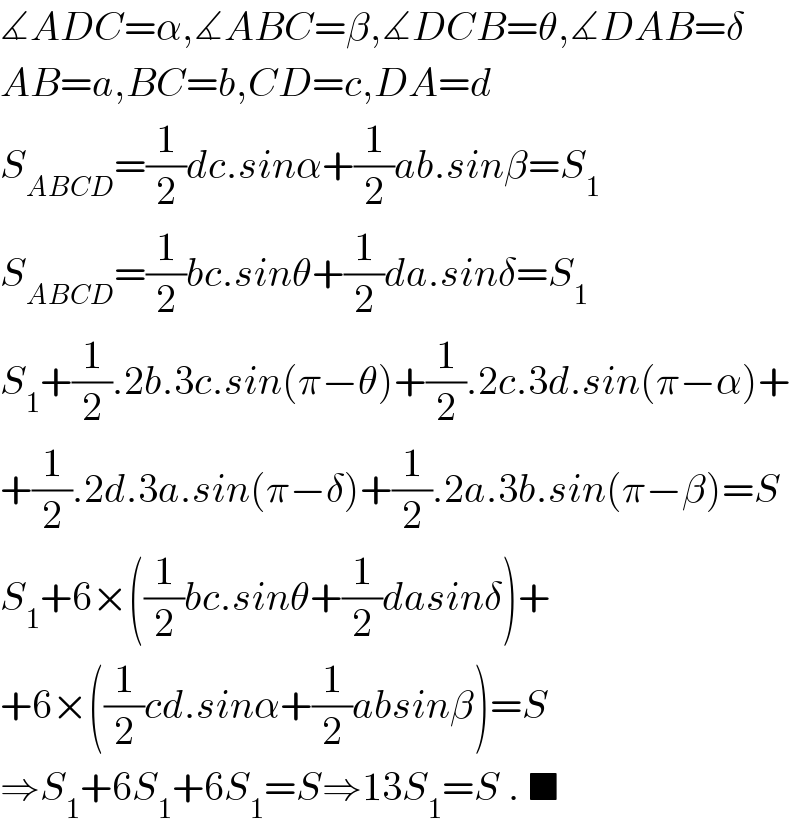
∡ADC=α,∡ABC=β,∡DCB=θ,∡DAB=δ AB=a,BC=b,CD=c,DA=d S_(ABCD) =(1/2)dc.sinα+(1/2)ab.sinβ=S_1 S_(ABCD) =(1/2)bc.sinθ+(1/2)da.sinδ=S_1 S_1 +(1/2).2b.3c.sin(π−θ)+(1/2).2c.3d.sin(π−α)+ +(1/2).2d.3a.sin(π−δ)+(1/2).2a.3b.sin(π−β)=S S_1 +6×((1/2)bc.sinθ+(1/2)dasinδ)+ +6×((1/2)cd.sinα+(1/2)absinβ)=S ⇒S_1 +6S_1 +6S_1 =S⇒13S_1 =S . ■

$$\measuredangle{ADC}=\alpha,\measuredangle{ABC}=\beta,\measuredangle{DCB}=\theta,\measuredangle{DAB}=\delta \\ $$$${AB}={a},{BC}={b},{CD}={c},{DA}={d} \\ $$$${S}_{{ABCD}} =\frac{\mathrm{1}}{\mathrm{2}}{dc}.{sin}\alpha+\frac{\mathrm{1}}{\mathrm{2}}{ab}.{sin}\beta={S}_{\mathrm{1}} \\ $$$${S}_{{ABCD}} =\frac{\mathrm{1}}{\mathrm{2}}{bc}.{sin}\theta+\frac{\mathrm{1}}{\mathrm{2}}{da}.{sin}\delta={S}_{\mathrm{1}} \\ $$$${S}_{\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{b}.\mathrm{3}{c}.{sin}\left(\pi−\theta\right)+\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{c}.\mathrm{3}{d}.{sin}\left(\pi−\alpha\right)+ \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{d}.\mathrm{3}{a}.{sin}\left(\pi−\delta\right)+\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{a}.\mathrm{3}{b}.{sin}\left(\pi−\beta\right)={S} \\ $$$${S}_{\mathrm{1}} +\mathrm{6}×\left(\frac{\mathrm{1}}{\mathrm{2}}{bc}.{sin}\theta+\frac{\mathrm{1}}{\mathrm{2}}{dasin}\delta\right)+ \\ $$$$+\mathrm{6}×\left(\frac{\mathrm{1}}{\mathrm{2}}{cd}.{sin}\alpha+\frac{\mathrm{1}}{\mathrm{2}}{absin}\beta\right)={S} \\ $$$$\Rightarrow{S}_{\mathrm{1}} +\mathrm{6}{S}_{\mathrm{1}} +\mathrm{6}{S}_{\mathrm{1}} ={S}\Rightarrow\mathrm{13}{S}_{\mathrm{1}} ={S}\:.\:\blacksquare \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17

in case of: n S_1 +2n(n+1)S_1 =S ⇒(S/S_1 )=2n^2 +2n+1 .■

$${in}\:{case}\:{of}:\:{n} \\ $$$${S}_{\mathrm{1}} +\mathrm{2}{n}\left({n}+\mathrm{1}\right){S}_{\mathrm{1}} ={S} \\ $$$$\Rightarrow\frac{{S}}{{S}_{\mathrm{1}} }=\mathrm{2}{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}\:.\blacksquare \\ $$

Commented by mrW1 last updated on 11/Jun/17

That′s right.

$$\mathrm{That}'\mathrm{s}\:\mathrm{right}. \\ $$

Answered by mrW1 last updated on 11/Jun/17

I have an other solution without using trigonometry and analytic geometry: A_(ΔBCF) =nA_(ΔACB) A_(ΔBGF) =(n+1)A_(ΔBCF) =(n+1)nA_(ΔACB) similarly A_(ΔDEH) =(n+1)nA_(ΔACD) ⇒A_(ΔBGF) +A_(ΔDEH) =(n+1)n(A_(ΔACB) +A_(ΔACD) )=(n+1)nA_(ABCD) similarly ⇒A_(ΔCHG) +A_(ΔAFE) =(n+1)n(A_(ΔCDB) +A_(ΔADB) )=(n+1)nA_(ABCD) A_(EFGH) =A_(ΔBGF) +A_(ΔDEH) +A_(ΔBGF) +A_(ΔDEH) +A_(ABCD) =2(n+1)nA_(ABCD) +A_(ABCD) =[2n(n+1)+1]A_(ABCD) =2n(n+1)+1 =2n^2 +2n+1

$$\mathrm{I}\:\mathrm{have}\:\mathrm{an}\:\mathrm{other}\:\:\mathrm{solution}\:\mathrm{without}\:\mathrm{using} \\ $$$$\mathrm{trigonometry}\:\mathrm{and}\:\mathrm{analytic}\:\mathrm{geometry}: \\ $$$$ \\ $$$$\mathrm{A}_{\Delta\mathrm{BCF}} =\mathrm{nA}_{\Delta\mathrm{ACB}} \\ $$$$\mathrm{A}_{\Delta\mathrm{BGF}} =\left(\mathrm{n}+\mathrm{1}\right)\mathrm{A}_{\Delta\mathrm{BCF}} =\left(\mathrm{n}+\mathrm{1}\right)\mathrm{nA}_{\Delta\mathrm{ACB}} \\ $$$$ \\ $$$$\mathrm{similarly} \\ $$$$\mathrm{A}_{\Delta\mathrm{DEH}} =\left(\mathrm{n}+\mathrm{1}\right)\mathrm{nA}_{\Delta\mathrm{ACD}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{A}_{\Delta\mathrm{BGF}} +\mathrm{A}_{\Delta\mathrm{DEH}} =\left(\mathrm{n}+\mathrm{1}\right)\mathrm{n}\left(\mathrm{A}_{\Delta\mathrm{ACB}} +\mathrm{A}_{\Delta\mathrm{ACD}} \right)=\left(\mathrm{n}+\mathrm{1}\right)\mathrm{nA}_{\mathrm{ABCD}} \\ $$$$ \\ $$$$\mathrm{similarly} \\ $$$$\Rightarrow\mathrm{A}_{\Delta\mathrm{CHG}} +\mathrm{A}_{\Delta\mathrm{AFE}} =\left(\mathrm{n}+\mathrm{1}\right)\mathrm{n}\left(\mathrm{A}_{\Delta\mathrm{CDB}} +\mathrm{A}_{\Delta\mathrm{ADB}} \right)=\left(\mathrm{n}+\mathrm{1}\right)\mathrm{nA}_{\mathrm{ABCD}} \\ $$$$ \\ $$$$\mathrm{A}_{\mathrm{EFGH}} =\mathrm{A}_{\Delta\mathrm{BGF}} +\mathrm{A}_{\Delta\mathrm{DEH}} +\mathrm{A}_{\Delta\mathrm{BGF}} +\mathrm{A}_{\Delta\mathrm{DEH}} +\mathrm{A}_{\mathrm{ABCD}} \\ $$$$=\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{nA}_{\mathrm{ABCD}} +\mathrm{A}_{\mathrm{ABCD}} \\ $$$$=\left[\mathrm{2n}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1}\right]\mathrm{A}_{\mathrm{ABCD}} \\ $$$$=\mathrm{2n}\left(\mathrm{n}+\mathrm{1}\right)+\mathrm{1} \\ $$$$=\mathrm{2n}^{\mathrm{2}} +\mathrm{2n}+\mathrm{1} \\ $$

Commented by mrW1 last updated on 11/Jun/17

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17

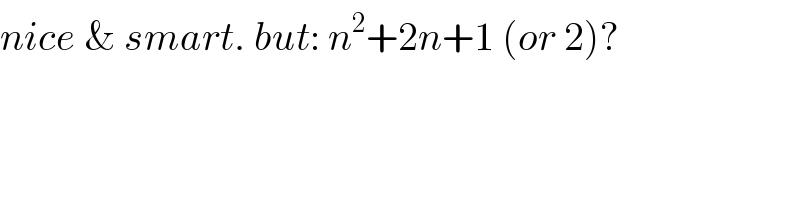
nice & smart. but: n^2 +2n+1 (or 2)?

$${nice}\:\&\:{smart}.\:{but}:\:{n}^{\mathrm{2}} +\mathrm{2}{n}+\mathrm{1}\:\left({or}\:\mathrm{2}\right)? \\ $$

Commented by mrW1 last updated on 11/Jun/17

thank you! 2n^2 +2n+1 is correct.

$$\mathrm{thank}\:\mathrm{you}!\:\mathrm{2n}^{\mathrm{2}} +\mathrm{2n}+\mathrm{1}\:\mathrm{is}\:\mathrm{correct}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com