Question Number 154437 by ArielVyny last updated on 18/Sep/21
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {arcos}\left(\frac{{cosx}}{\mathrm{1}+\mathrm{2}{cosx}}\right){dx} \\ $$
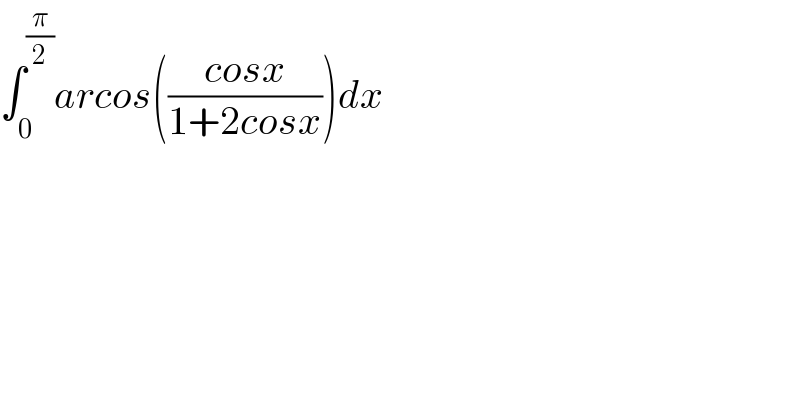
Answered by phanphuoc last updated on 18/Sep/21
$${put}\:{x}={tan}\left({t}/\mathrm{2}\right) \\ $$$$ \\ $$
Answered by Kamel last updated on 18/Sep/21
$$\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{24}} \\ $$
Answered by puissant last updated on 18/Sep/21
![Q=∫_0 ^(π/2) arccos(((cosx)/(1+2cosx)))dx=2∫_0 ^(π/2) arccos((√((1+((cosx)/(1+2cosx)))/2)))dx =2∫_0 ^(π/2) arctan((√((1+cosx)/(1+3cosx))))dx=4∫_0 ^(π/4) arctan((√((1+cos2u)/(1+3cos2u))))du Diver: ′′1+cos2u=2cosu et cos2u=1−sin^2 u (Trivial)′′ ⇒ Q=4∫_0 ^(π/4) arctan((√((cos^2 u)/(1−sin^2 u))))du=4∫_0 ^(π/4) arctan(((cosu)/( (√(1−2sinu)))))du =4∫_0 ^(π/4) ∫_0 ^1 (((√(2−3sin^2 u)) cosu)/((x^2 +2)−sin^2 u(x^2 +3)))dxdu (√3)sinu=(√2)sinθ → cosudu=((√2)/( (√3)))cosθdθ ⇒ Q=4∫_0 ^(π/3) ∫_0 ^1 ((2(√3) cos^2 θ)/(3x^2 +6−2(1−cos^2 θ)(x^2 +3)))dxdθ =^(t=tanu) 8(√3)∫_0 ^(√3) ∫_0 ^1 (1/((1+t^2 )(t^2 x^2 +3x^2 +6)))dxdt =8(√3)∫_0 ^(√3) ∫_0 ^1 (((−(1/(2x^2 +6)))/(1+t^2 ))+((x^2 /(2x^2 +6))/(t^2 x^2 +3x^2 +6)))dxdt=8(√3)∫_0 ^1 (1/(2x^2 +6))(∫_0 ^(√3) (dt/(1+t^2 ))−∫_0 ^(√3) (dt/(t^2 +3+(6/x^2 ))))dx =((2π^2 )/9)−4[arctan((x/( (√(x^2 +2)))))arctan((√(x^2 +2)))]_0 ^1 +4∫_0 ^1 ((arctan((√(x^2 +2))))/((x^2 +1)(√(x^2 +1))))dx =4∫_0 ^1 ((arctan((√(x^2 +2))))/((x^2 +1)(√(x^2 +1))))dx = 4×((5π^2 )/(96)) = ((5π^2 )/(24)).. ∵∴ Q = ((5π^2 )/(24))... ......................Le puissant......................](Q154472.png)
$${Q}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {arccos}\left(\frac{{cosx}}{\mathrm{1}+\mathrm{2}{cosx}}\right){dx}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {arccos}\left(\sqrt{\frac{\mathrm{1}+\frac{{cosx}}{\mathrm{1}+\mathrm{2}{cosx}}}{\mathrm{2}}}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {arctan}\left(\sqrt{\frac{\mathrm{1}+{cosx}}{\mathrm{1}+\mathrm{3}{cosx}}}\right){dx}=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {arctan}\left(\sqrt{\frac{\mathrm{1}+{cos}\mathrm{2}{u}}{\mathrm{1}+\mathrm{3}{cos}\mathrm{2}{u}}}\right){du} \\ $$$${Diver}:\:''\mathrm{1}+{cos}\mathrm{2}{u}=\mathrm{2}{cosu}\:{et}\:{cos}\mathrm{2}{u}=\mathrm{1}−{sin}^{\mathrm{2}} {u}\:\left({Trivial}\right)'' \\ $$$$\Rightarrow\:{Q}=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {arctan}\left(\sqrt{\frac{{cos}^{\mathrm{2}} {u}}{\mathrm{1}−{sin}^{\mathrm{2}} {u}}}\right){du}=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {arctan}\left(\frac{{cosu}}{\:\sqrt{\mathrm{1}−\mathrm{2}{sinu}}}\right){du} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{2}−\mathrm{3}{sin}^{\mathrm{2}} {u}}\:{cosu}}{\left({x}^{\mathrm{2}} +\mathrm{2}\right)−{sin}^{\mathrm{2}} {u}\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dxdu} \\ $$$$\sqrt{\mathrm{3}}{sinu}=\sqrt{\mathrm{2}}{sin}\theta\:\rightarrow\:{cosudu}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}{cos}\theta{d}\theta \\ $$$$\Rightarrow\:{Q}=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}\sqrt{\mathrm{3}}\:{cos}^{\mathrm{2}} \theta}{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{6}−\mathrm{2}\left(\mathrm{1}−{cos}^{\mathrm{2}} \theta\right)\left({x}^{\mathrm{2}} +\mathrm{3}\right)}{dxd}\theta \\ $$$$\overset{{t}={tanu}} {=}\:\mathrm{8}\sqrt{\mathrm{3}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{6}\right)}{dxdt} \\ $$$$=\mathrm{8}\sqrt{\mathrm{3}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}}}{{t}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{6}}\right){dxdt}=\mathrm{8}\sqrt{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{6}}\left(\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }−\int_{\mathrm{0}} ^{\sqrt{\mathrm{3}}} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{3}+\frac{\mathrm{6}}{{x}^{\mathrm{2}} }}\right){dx} \\ $$$$=\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{9}}−\mathrm{4}\left[{arctan}\left(\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}}\right){arctan}\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arctan}\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arctan}\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dx}\:=\:\mathrm{4}×\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{96}}\:=\:\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{24}}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\because\therefore\:\:\:\:\:{Q}\:=\:\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{24}}...\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......................\mathscr{L}{e}\:{puissant}...................... \\ $$
Commented by peter frank last updated on 18/Sep/21
$$\mathrm{good} \\ $$
Commented by ArielVyny last updated on 19/Sep/21
$${thank}\:{sir} \\ $$