Question Number 154478 by mnjuly1970 last updated on 18/Sep/21
$$ \\ $$$$ \\ $$$$\:\:{prove}\:{that}\:# \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{sin}^{\:\mathrm{3}} \left(\:{x}\:\right).{ln}\left(\:{x}\:\right)}{{x}}\:{dx}\:\overset{?} {=}\:\frac{\pi}{\mathrm{8}}\:\left(−\mathrm{2}\gamma\:+{ln}\left(\mathrm{3}\right)\right)\:.....\blacksquare\:{m}.{n}\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\: \\ $$$$ \\ $$
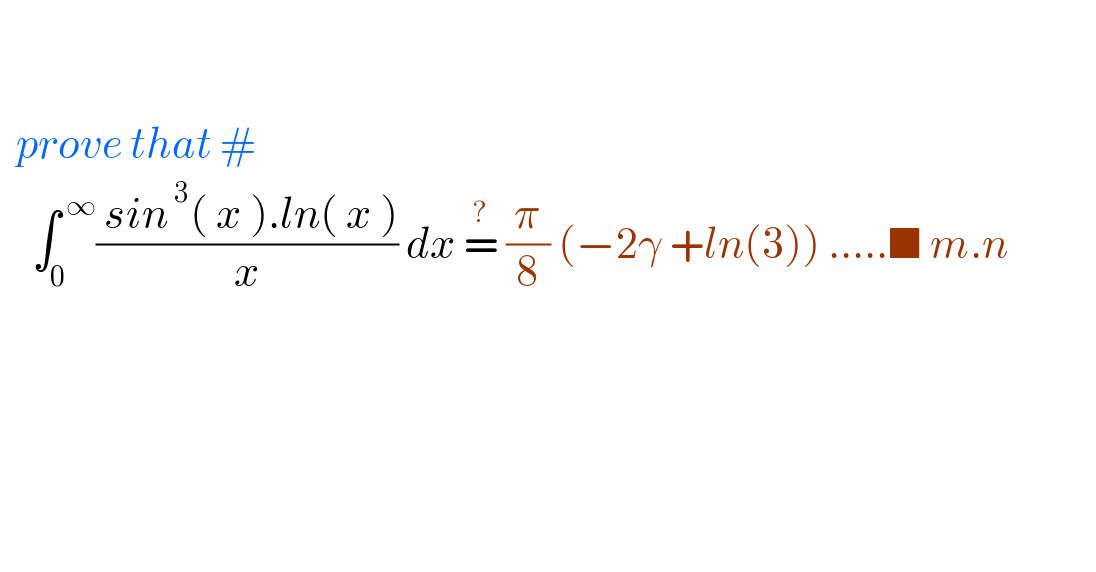
Answered by ARUNG_Brandon_MBU last updated on 18/Sep/21
![∫_0 ^∞ ((sin^3 x∙lnx)/x)dx 2isinx=(e^(ix) −e^(−ix) ) −8isin^3 x=e^(3ix) −3e^(ix) +3e^(−ix) −e^(−3ix) sin^3 x=(3/4)sinx−(1/4)sin3x Ω(α)=−∫_0 ^∞ ((sin^3 x)/x^α )=(1/4)∫_0 ^∞ (((sin3x)/x^α )−((3sinx)/x^α ))dx=(1/4)[((π3^(α−1) −3π)/(2Γ(α)sin((π/2)α)))] Ω′(α)=(1/8)[((π3^(α−1) ln3(Γ(α)sin((π/2)α))−(π3^(α−1) −3π)((π/2)cos((π/2)α)Γ(α)+sin((π/2)α)Γ′(α)))/(Γ^2 (α)sin^2 ((π/2)α)))] Ω′(1)=∫_0 ^∞ ((sin^3 x∙lnx)/x)dx=(1/8)[((πln3+2π(Γ′(1)))/(Γ^2 (1)sin^2 ((π/2))))]=(1/8)(πln3−2πγ)=(π/8)(ln3−2γ)](Q154488.png)
$$\:\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{3}} {x}\centerdot\mathrm{ln}{x}}{{x}}{dx} \\ $$$$\mathrm{2}{i}\mathrm{sin}{x}=\left({e}^{{ix}} −{e}^{−{ix}} \right) \\ $$$$−\mathrm{8}{i}\mathrm{sin}^{\mathrm{3}} {x}={e}^{\mathrm{3}{ix}} −\mathrm{3}{e}^{{ix}} +\mathrm{3}{e}^{−{ix}} −{e}^{−\mathrm{3}{ix}} \\ $$$$\mathrm{sin}^{\mathrm{3}} {x}=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}{x}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin3}{x} \\ $$$$\Omega\left(\alpha\right)=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{3}} {x}}{{x}^{\alpha} }=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{sin3}{x}}{{x}^{\alpha} }−\frac{\mathrm{3sin}{x}}{{x}^{\alpha} }\right){dx}=\frac{\mathrm{1}}{\mathrm{4}}\left[\frac{\pi\mathrm{3}^{\alpha−\mathrm{1}} −\mathrm{3}\pi}{\mathrm{2}\Gamma\left(\alpha\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\alpha\right)}\right] \\ $$$$\Omega'\left(\alpha\right)=\frac{\mathrm{1}}{\mathrm{8}}\left[\frac{\pi\mathrm{3}^{\alpha−\mathrm{1}} \mathrm{ln3}\left(\Gamma\left(\alpha\right)\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\alpha\right)\right)−\left(\pi\mathrm{3}^{\alpha−\mathrm{1}} −\mathrm{3}\pi\right)\left(\frac{\pi}{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}\alpha\right)\Gamma\left(\alpha\right)+\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}\alpha\right)\Gamma'\left(\alpha\right)\right)}{\Gamma^{\mathrm{2}} \left(\alpha\right)\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\alpha\right)}\right] \\ $$$$\Omega'\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}^{\mathrm{3}} {x}\centerdot\mathrm{ln}{x}}{{x}}{dx}=\frac{\mathrm{1}}{\mathrm{8}}\left[\frac{\pi\mathrm{ln3}+\mathrm{2}\pi\left(\Gamma'\left(\mathrm{1}\right)\right)}{\Gamma^{\mathrm{2}} \left(\mathrm{1}\right)\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\right)}\right]=\frac{\mathrm{1}}{\mathrm{8}}\left(\pi\mathrm{ln3}−\mathrm{2}\pi\gamma\right)=\frac{\pi}{\mathrm{8}}\left(\mathrm{ln3}−\mathrm{2}\gamma\right) \\ $$
Commented by mnjuly1970 last updated on 18/Sep/21
$${thank}\:{you}\:{so}\:{much}\:{sir}\:\mathrm{A}{rung}.. \\ $$
Commented by Ar Brandon last updated on 18/Sep/21
My pleasure, Sir ��