
Question and Answers Forum
Question Number 154649 by mathdanisur last updated on 20/Sep/21
![if n ∈ N^(>2) prove that [((n)^(1/3) + ((n + 2))^(1/3) )^3 ] + 1 = 0 (mod 8)](Q154649.png)
Commented byMJS_new last updated on 20/Sep/21
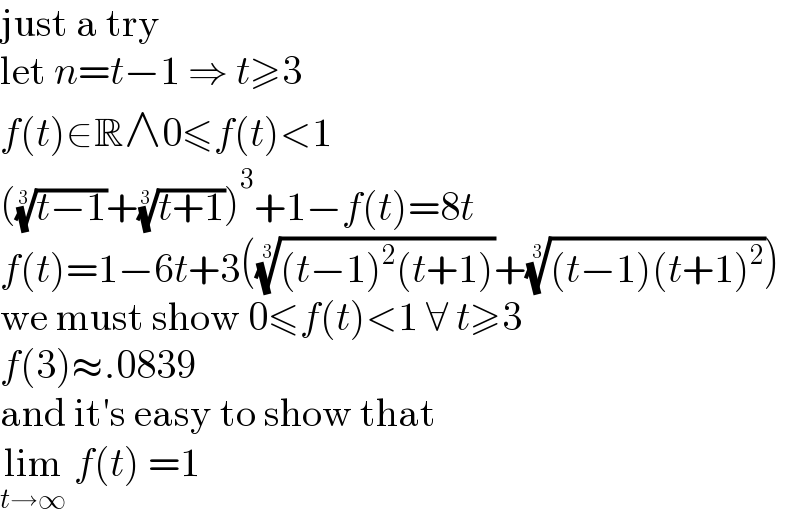
Commented bymathdanisur last updated on 20/Sep/21

| ||
Question and Answers Forum | ||
Question Number 154649 by mathdanisur last updated on 20/Sep/21 | ||
![if n ∈ N^(>2) prove that [((n)^(1/3) + ((n + 2))^(1/3) )^3 ] + 1 = 0 (mod 8)](Q154649.png) | ||
Commented byMJS_new last updated on 20/Sep/21 | ||
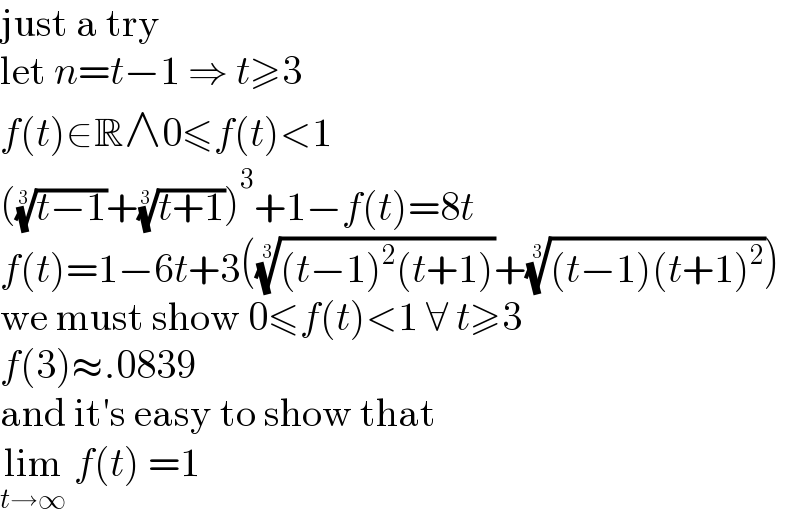 | ||
Commented bymathdanisur last updated on 20/Sep/21 | ||
 | ||