Question Number 154669 by SANOGO last updated on 20/Sep/21
Answered by ARUNG_Brandon_MBU last updated on 20/Sep/21
![I=∫_0 ^1 (dt/( (√(1+t^2 ))+(√(1−t^2 ))))=(1/2)∫_0 ^1 ((√(1+t^2 ))−(√(1−t^2 )))dt =(1/2)∫_0 ^(argsh(1)) cosh^2 ϑdϑ−(1/2)∫_0 ^(π/2) cos^2 ϑdϑ =(1/4)∫_0 ^(argsh(1)) (1+cosh2ϑ)dϑ−(1/4)∫_0 ^(π/2) (cos2ϑ+1)dϑ =(1/4)argsh(1)+[((sinh2ϑ)/8)]_0 ^(argsh(1)) −(1/4)[((sin2ϑ)/2)+ϑ]_0 ^(π/2) =(1/4)ln(1+(√2))+((√2)/4)−(π/8)](Q154681.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\right){dt} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{1}\right)} \mathrm{cosh}^{\mathrm{2}} \vartheta{d}\vartheta−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} \vartheta{d}\vartheta \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{1}\right)} \left(\mathrm{1}+\mathrm{cosh2}\vartheta\right){d}\vartheta−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{cos2}\vartheta+\mathrm{1}\right){d}\vartheta \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{argsh}\left(\mathrm{1}\right)+\left[\frac{\mathrm{sinh2}\vartheta}{\mathrm{8}}\right]_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{1}\right)} −\frac{\mathrm{1}}{\mathrm{4}}\left[\frac{\mathrm{sin2}\vartheta}{\mathrm{2}}+\vartheta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}−\frac{\pi}{\mathrm{8}} \\ $$
Commented by ARUNG_Brandon_MBU last updated on 20/Sep/21
$$\mathrm{Ah}\:\mathrm{oui}\:!\:\mathrm{merci}. \\ $$
Commented by puissant last updated on 20/Sep/21
$${Broo}\:{attention}\:!!!! \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{2}{t}^{\mathrm{2}} }.. \\ $$
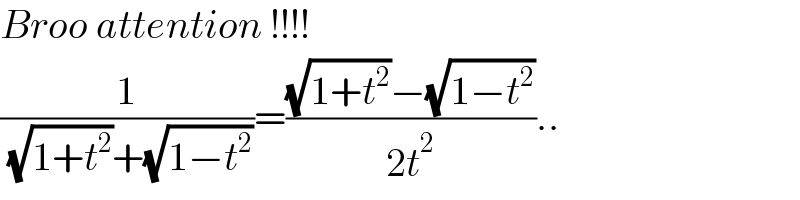
Commented by SANOGO last updated on 20/Sep/21
$${supere}\:{demonstratin} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 20/Sep/21
![I=∫_0 ^1 (dt/( (√(1+t^2 ))+(√(1−t^2 ))))=∫_0 ^1 (((√(1+t^2 ))−(√(1−t^2 )))/(2t^2 ))dt =(1/2)∫_0 ^(argsh(1)) ((cosh^2 ϑ)/(sinh^2 ϑ))dϑ−(1/2)∫_0 ^(π/2) ((cos^2 ϑ)/(sin^2 ϑ))dϑ =(1/2)∫_0 ^(argsh(1)) (cosech^2 ϑ+1)dϑ−(1/2)∫_0 ^(π/2) (csc^2 ϑ−1)dϑ =(1/2)[ϑ−cothϑ]_0 ^(argsh(1)) +(1/2)[cotϑ+ϑ]_0 ^(π/2) =(1/2)ln(1+(√2))−((√2)/2)+(π/4)](Q154695.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }−\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{2}{t}^{\mathrm{2}} }{dt} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{1}\right)} \frac{\mathrm{cosh}^{\mathrm{2}} \vartheta}{\mathrm{sinh}^{\mathrm{2}} \vartheta}{d}\vartheta−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}^{\mathrm{2}} \vartheta}{\mathrm{sin}^{\mathrm{2}} \vartheta}{d}\vartheta \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{1}\right)} \left(\mathrm{cosech}^{\mathrm{2}} \vartheta+\mathrm{1}\right){d}\vartheta−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{csc}^{\mathrm{2}} \vartheta−\mathrm{1}\right){d}\vartheta \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\vartheta−\mathrm{coth}\vartheta\right]_{\mathrm{0}} ^{\mathrm{argsh}\left(\mathrm{1}\right)} +\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{cot}\vartheta+\vartheta\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}} \\ $$
Commented by SANOGO last updated on 20/Sep/21
$${merci}\:{bien}\:{mon}\:{grand} \\ $$