
Question and Answers Forum
Question Number 15480 by ajfour last updated on 10/Jun/17
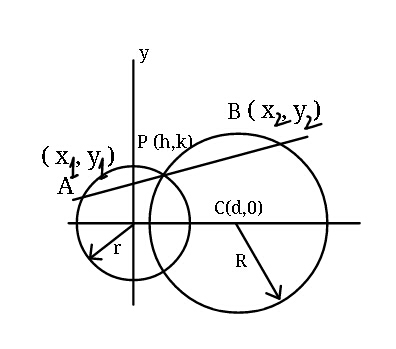
Commented by ajfour last updated on 10/Jun/17
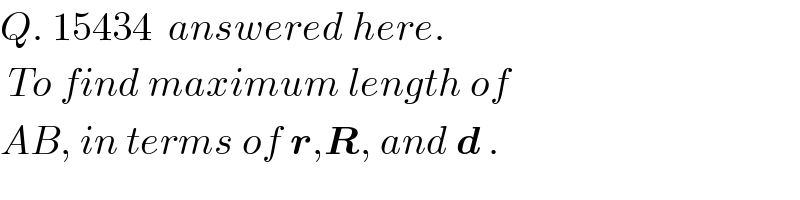
Answered by ajfour last updated on 11/Jun/17
![To find P(h,k). x^2 +y^2 =r^2 (x−d)^2 +y^2 =R^2 subtracting to obtain h 2dh=R^2 −r^2 h=((R^2 −r^2 )/(2d)) k= (√(r^2 −h^2 )) (considering just the positive one here) let equation of APB be, y=m(x−h)+k solving this with x^2 +y^2 =r^2 x^2 +[m(x−h)+k]^2 −r^2 =0 (1+m^2 )x^2 +(−2m^2 h+2mk)x+c_1 =0 its roots are h and x_1 . so x_1 +h=−(((−2m^2 h+2mk)/(1+m^2 ))) ...(i) Again solving line y=m(x−h)+k witb (x−d)^2 +y^2 =R^2 (x−d)^2 +[m(x−h)+k]^2 −R^2 =0 (1+m^2 )x^2 +(−2d−2m^2 h+2mk)x+c_2 =0 its roots are h, and x_2 . x_2 +h=−(((−2d−2m^2 h+2mk)/(1+m^2 ))) ..(ii) eqn. (i)−eqn.(ii) gives: x_2 −x_1 =((2d)/(1+m^2 )) length of AB = (√(1+m^2 ))(x_2 −x_1 ) l_(AB) = ((2d)/(√(1+m^2 ))) and is clearly maximum for m=0, and (length AB)_(max) = 2d .](Q15482.png)
Commented by mrW1 last updated on 11/Jun/17

| ||
Question and Answers Forum | ||
Question Number 15480 by ajfour last updated on 10/Jun/17 | ||
 | ||
Commented by ajfour last updated on 10/Jun/17 | ||
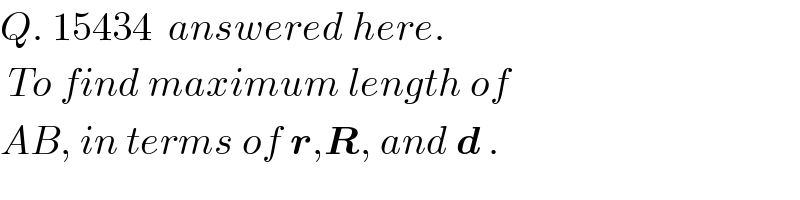 | ||
Answered by ajfour last updated on 11/Jun/17 | ||
![To find P(h,k). x^2 +y^2 =r^2 (x−d)^2 +y^2 =R^2 subtracting to obtain h 2dh=R^2 −r^2 h=((R^2 −r^2 )/(2d)) k= (√(r^2 −h^2 )) (considering just the positive one here) let equation of APB be, y=m(x−h)+k solving this with x^2 +y^2 =r^2 x^2 +[m(x−h)+k]^2 −r^2 =0 (1+m^2 )x^2 +(−2m^2 h+2mk)x+c_1 =0 its roots are h and x_1 . so x_1 +h=−(((−2m^2 h+2mk)/(1+m^2 ))) ...(i) Again solving line y=m(x−h)+k witb (x−d)^2 +y^2 =R^2 (x−d)^2 +[m(x−h)+k]^2 −R^2 =0 (1+m^2 )x^2 +(−2d−2m^2 h+2mk)x+c_2 =0 its roots are h, and x_2 . x_2 +h=−(((−2d−2m^2 h+2mk)/(1+m^2 ))) ..(ii) eqn. (i)−eqn.(ii) gives: x_2 −x_1 =((2d)/(1+m^2 )) length of AB = (√(1+m^2 ))(x_2 −x_1 ) l_(AB) = ((2d)/(√(1+m^2 ))) and is clearly maximum for m=0, and (length AB)_(max) = 2d .](Q15482.png) | ||
| ||
Commented by mrW1 last updated on 11/Jun/17 | ||
 | ||