∫_(π/2) ^(π/4) sin^3 (x)cos^2 (x)dx


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 154877 by SANOGO last updated on 22/Sep/21

$\int_{\frac{π}{2}}^{\frac{π}{4}} {s i n}^{3} (x) {c o s}^{2} (x) d x$
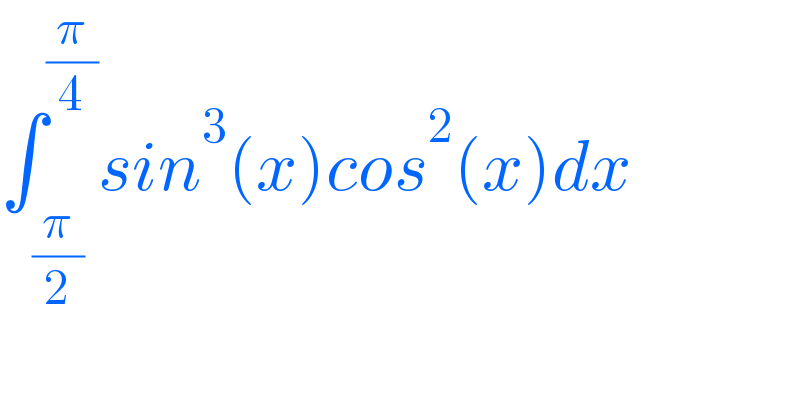
Commented by saly last updated on 24/Sep/21

$t h a n k y o u$
	Answered by Mr.D.N. last updated on 22/Sep/21
	$∫_(π/2) ^( (π/4)) sin^3 (x) cos^2 (x) dx ∫_(π/2) ^( (π/4)) sin^2 x.cos^2 x. sin x dx ∫_(π/2) ^( (π/4)) (1−cos^2 x)cos^2 x sinx dx put cos x= t −sin x dx =dt sin x dx= −dt change limit, if x=(π/4) then t= (1/( (√2))) if x= (π/2) then t= 0 −∫_0 ^( (1/( (√2)))) (1−t^2 )t^2 dt ∫_0 ^(1/( (√2))) ( t^4 −t^2 )dt = [(t^5 /5)−(t^3 /3)]_0 ^(1/( (√2))) = [t^3 ((1/5)t^2 −(1/3))]_0 ^(1/(√2)) = [ ((1/( (√2))))^3 {(1/5)((√2) )^2 −(1/3)}]−0 = (1/( (√2)))×(1/2)((2/5)−(1/3)) = (1/( 2(√2)))(((6−5)/(15)))=(1/(30(√2))) //.$
	$\int_{\frac{π}{2}}^{\frac{π}{4}} \sin^{3} (x) \cos^{2} (x) dx$ $\int_{\frac{π}{2}}^{\frac{π}{4}} \sin^{2} x . \cos^{2} x . \sin x dx$ $\int_{\frac{π}{2}}^{\frac{π}{4}} (1 - \cos^{2} x) \cos^{2} x sinx dx$ $put \cos x = t$ $- \sin x dx = dt$ $\sin x dx = - dt$ $change limit,$ $if x = \frac{π}{4} then t = \frac{1}{\sqrt{2}}$ $if x = \frac{π}{2} then t = 0$ $- \int_{0}^{\frac{1}{\sqrt{2}}} (1 - t^{2}) t^{2} dt$ $\int_{0}^{\frac{1}{\sqrt{2}}} (t^{4} - t^{2}) dt$ $= {[\frac{t^{5}}{5} - \frac{t^{3}}{3}]}_{0}^{\frac{1}{\sqrt{2}}}$ $= {[t^{3} (\frac{1}{5} t^{2} - \frac{1}{3})]}_{0}^{1 / \sqrt{2}}$ $= [{(\frac{1}{\sqrt{2}})}^{3} {\frac{1}{5} {(\sqrt{2})}^{2} - \frac{1}{3}}] - 0$ $= \frac{1}{\sqrt{2}} \times \frac{1}{2} (\frac{2}{5} - \frac{1}{3})$ $= \frac{1}{2 \sqrt{2}} (\frac{6 - 5}{15}) = \frac{1}{30 \sqrt{2}} / / .$
	Commented by SANOGO last updated on 23/Sep/21

	$m e r c i b i e n$
	Answered by Ar Brandon last updated on 23/Sep/21

	$I = \int_{\frac{π}{2}}^{\frac{π}{4}} \sin^{3} x \cos^{2} x d x = \int_{\frac{π}{2}}^{\frac{π}{4}} \sin x (\cos^{2} x - \cos^{4} x) d x$ $= \int_{\frac{π}{2}}^{\frac{π}{4}} (\cos^{4} x - \cos^{2} x) d (\cos x) = {[\frac{\cos^{5} x}{5} - \frac{\cos^{3} x}{3}]}_{\frac{π}{2}}^{\frac{π}{4}}$ $= \frac{1}{5 \sqrt{2^{5}}} - \frac{1}{3 \sqrt{2^{3}}} = \frac{1}{20 \sqrt{2}} - \frac{1}{6 \sqrt{2}} = - \frac{7 \sqrt{2}}{120}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum