
Question and Answers Forum
Question Number 155496 by mathocean1 last updated on 01/Oct/21
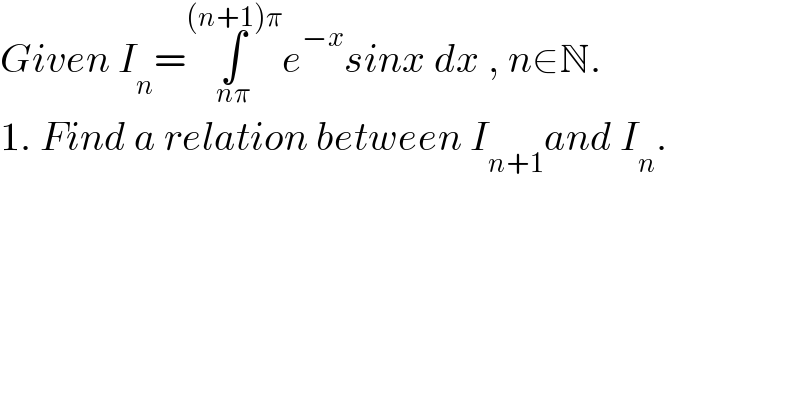
Answered by ArielVyny last updated on 01/Oct/21
![I_n =∫_(nπ) ^((n+1)π) e^(−x) sinxdx du=e^(−x) →u=−e^(−x) v=sinx→dv=cosx I_n =[−e^(−x) sinx]_(nπ) ^((n+1)π) +∫_(nπ) ^((n+1)) e^(−x) cosxdx du=e^(−x) →u=−e^(−x) v=cosx→dv=−sinx 2I_n =−[e^(−x) sinx+e^(−x) cosx]_(nπ) ^((n+1)π) 2I_n =−[e^(−π(n+1)) sin((n+1)π)+e^(−π(n+1)) cos((n+1)π)−e^(−nπ) sin(nπ)−e^(−nπ) cos(nπ)] 2I_n =−[e^(−π(n+1)) (sin(nπ)cosπ+cos(nπ)sinπ)+e^(−π(n+1)) (cosnπcosπ+sin(nπ)sin(π)−e^(−nπ) sin(nπ)−e^(−nπ) cos(nπ)] 2I_n =−[−e^(−π(n+1)) (−1)^n −e^(−nπ) (−1)^n ] 2I_n =(−1)^n e^(−π(n+1)) +(−1)^n e^(−nπ) 2I_(n+1) =(−1)^(n+1) e^(−π(n+2)) +(−1)^n e^(−(n+1)π) 2I_(n+1) −2I_n =(−1)^(n+1) e^(−π(n+2)) +(−1)^(n+1) e^(−nπ) I_(n+1) −I_n =(((−1)^(n+1) e^(−π(n+2)) +(−1)^(n+1) e^(−nπ) )/2)](Q155534.png)
Commented by mathocean1 last updated on 22/Oct/21

| ||
Question and Answers Forum | ||
Question Number 155496 by mathocean1 last updated on 01/Oct/21 | ||
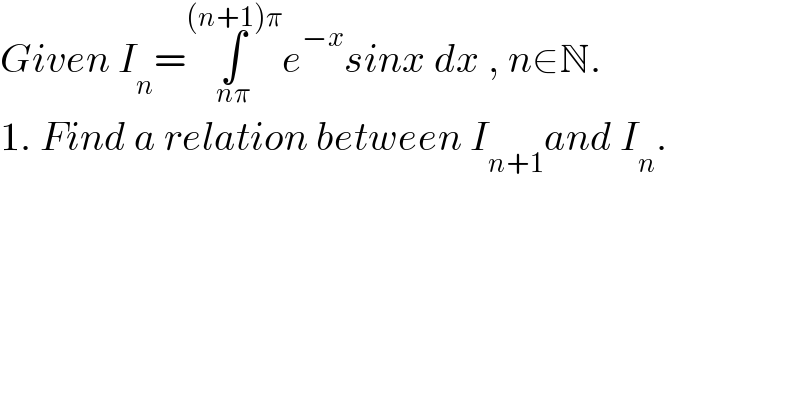 | ||
Answered by ArielVyny last updated on 01/Oct/21 | ||
![I_n =∫_(nπ) ^((n+1)π) e^(−x) sinxdx du=e^(−x) →u=−e^(−x) v=sinx→dv=cosx I_n =[−e^(−x) sinx]_(nπ) ^((n+1)π) +∫_(nπ) ^((n+1)) e^(−x) cosxdx du=e^(−x) →u=−e^(−x) v=cosx→dv=−sinx 2I_n =−[e^(−x) sinx+e^(−x) cosx]_(nπ) ^((n+1)π) 2I_n =−[e^(−π(n+1)) sin((n+1)π)+e^(−π(n+1)) cos((n+1)π)−e^(−nπ) sin(nπ)−e^(−nπ) cos(nπ)] 2I_n =−[e^(−π(n+1)) (sin(nπ)cosπ+cos(nπ)sinπ)+e^(−π(n+1)) (cosnπcosπ+sin(nπ)sin(π)−e^(−nπ) sin(nπ)−e^(−nπ) cos(nπ)] 2I_n =−[−e^(−π(n+1)) (−1)^n −e^(−nπ) (−1)^n ] 2I_n =(−1)^n e^(−π(n+1)) +(−1)^n e^(−nπ) 2I_(n+1) =(−1)^(n+1) e^(−π(n+2)) +(−1)^n e^(−(n+1)π) 2I_(n+1) −2I_n =(−1)^(n+1) e^(−π(n+2)) +(−1)^(n+1) e^(−nπ) I_(n+1) −I_n =(((−1)^(n+1) e^(−π(n+2)) +(−1)^(n+1) e^(−nπ) )/2)](Q155534.png) | ||
| ||
Commented by mathocean1 last updated on 22/Oct/21 | ||
 | ||