Question Number 155571 by peter frank last updated on 02/Oct/21
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{one}\:.\mathrm{Hence} \\ $$$$\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{root}\:\mathrm{is}\: \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{zero} \\ $$
Answered by JDamian last updated on 02/Oct/21
$${z}^{\mathrm{3}} =\mathrm{1} \\ $$$$\left\{{z}\right\}=\left\{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}{k}} \right\}_{\mathrm{0}\leqslant{k}<\mathrm{3}} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}} {\sum}}{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}{k}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}} {\sum}}\left({e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)^{{k}} =\frac{\left({e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} −\mathrm{1}}{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} −\mathrm{1}}=\frac{{e}^{{i}\mathrm{2}\pi} −\mathrm{1}}{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} −\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}−\mathrm{1}}{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} −\mathrm{1}}=\mathrm{0} \\ $$
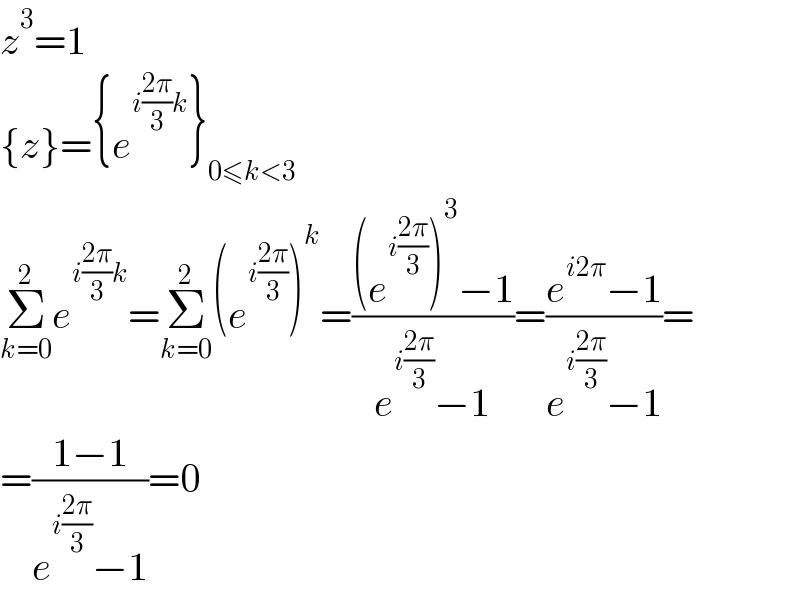
Commented by peter frank last updated on 02/Oct/21
$$\mathrm{great}\:\mathrm{sir}\:;\mathrm{thanks} \\ $$
Commented by puissant last updated on 02/Oct/21
$${Nice}\:{sir}..\:{but}\:{it}\:{is}\:{rather}\:{k}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2}\right\}.. \\ $$
Answered by puissant last updated on 02/Oct/21
![z^3 =1 ⇒ z=e^(i((2kπ)/3)) ; k∈[∣ 0;2 ∣] → k=0 ⇒ z= 1 → k=1 ⇒ z=e^(i((2π)/3)) →k=2 ⇒ z=e^(i((4π)/3)) = e^(−i((2π)/3)) let j=e^(i((2π)/3)) 1+j+j^2 = ((1−j^3 )/(1−j))= (((e^(i((2π)/3)) )^3 −1)/(e^(i((2π)/3)) −1))= 0... −−−−−−−−−−−−− j=e^(i((2π)/3)) = −(1/2)+((√3)/2)i and j^2 =e^(i((4π)/3)) = e^(−i((2π)/3)) = −(1/2)−((√3)/2)i.. 1+j+j^2 = 1−(1/2)+((√3)/2)i−(1/2)−((√3)/2)i=1−1=0 ⇒ 1+j+j^2 = 0...](Q155588.png)
$${z}^{\mathrm{3}} =\mathrm{1}\:\Rightarrow\:{z}={e}^{{i}\frac{\mathrm{2}{k}\pi}{\mathrm{3}}} \:;\:\:{k}\in\left[\mid\:\mathrm{0};\mathrm{2}\:\mid\right] \\ $$$$\rightarrow\:{k}=\mathrm{0}\:\Rightarrow\:{z}=\:\mathrm{1} \\ $$$$\rightarrow\:{k}=\mathrm{1}\:\Rightarrow\:{z}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\rightarrow{k}=\mathrm{2}\:\Rightarrow\:{z}={e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} =\:{e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${let}\:{j}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$\mathrm{1}+{j}+{j}^{\mathrm{2}} =\:\frac{\mathrm{1}−{j}^{\mathrm{3}} }{\mathrm{1}−{j}}=\:\frac{\left({e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} −\mathrm{1}}{{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} −\mathrm{1}}=\:\mathrm{0}... \\ $$$$−−−−−−−−−−−−− \\ $$$${j}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:=\:−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\:{and}\: \\ $$$${j}^{\mathrm{2}} ={e}^{{i}\frac{\mathrm{4}\pi}{\mathrm{3}}} =\:{e}^{−{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} =\:−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}.. \\ $$$$\mathrm{1}+{j}+{j}^{\mathrm{2}} =\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}=\mathrm{1}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{1}+{j}+{j}^{\mathrm{2}} =\:\mathrm{0}... \\ $$