Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 155576 by MathsFan last updated on 02/Oct/21

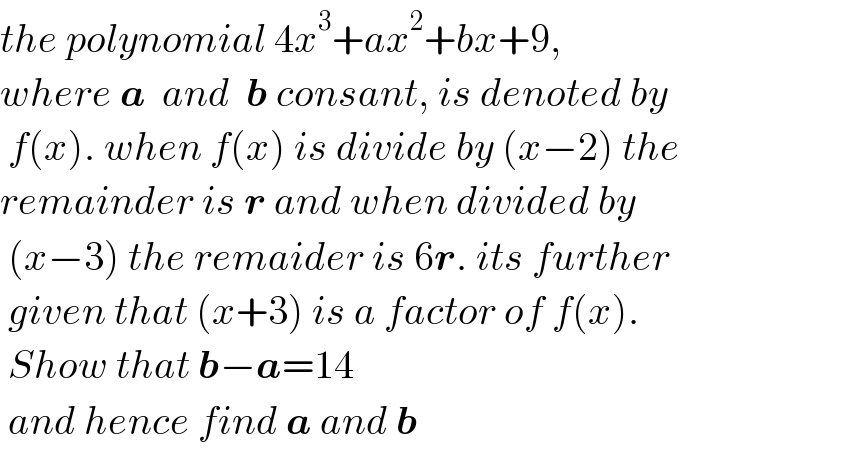
the polynomial 4x^3 +ax^2 +bx+9, where a and b consant, is denoted by f(x). when f(x) is divide by (x−2) the remainder is r and when divided by (x−3) the remaider is 6r. its further given that (x+3) is a factor of f(x). Show that b−a=14 and hence find a and b

$${the}\:{polynomial}\:\mathrm{4}{x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+\mathrm{9}, \\ $$$${where}\:\boldsymbol{{a}}\:\:{and}\:\:\boldsymbol{{b}}\:{consant},\:{is}\:{denoted}\:{by} \\ $$$$\:{f}\left({x}\right).\:{when}\:{f}\left({x}\right)\:{is}\:{divide}\:{by}\:\left({x}−\mathrm{2}\right)\:{the} \\ $$$${remainder}\:{is}\:\boldsymbol{{r}}\:{and}\:{when}\:{divided}\:{by} \\ $$$$\:\left({x}−\mathrm{3}\right)\:{the}\:{remaider}\:{is}\:\mathrm{6}\boldsymbol{{r}}.\:{its}\:{further} \\ $$$$\:{given}\:{that}\:\left({x}+\mathrm{3}\right)\:{is}\:{a}\:{factor}\:{of}\:{f}\left({x}\right). \\ $$$$\:{Show}\:{that}\:\boldsymbol{{b}}−\boldsymbol{{a}}=\mathrm{14} \\ $$$$\:{and}\:{hence}\:{find}\:\boldsymbol{{a}}\:{and}\:\boldsymbol{{b}} \\ $$

Commented by Rasheed.Sindhi last updated on 02/Oct/21

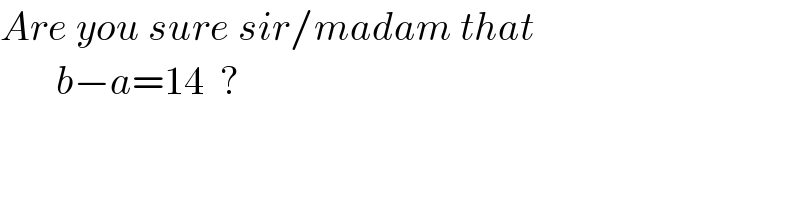
Are you sure sir/madam that b−a=14 ?

$${Are}\:{you}\:{sure}\:{sir}/{madam}\:{that} \\ $$$$\:\:\:\:\:\:\:{b}−{a}=\mathrm{14}\:\:? \\ $$

Commented by MathsFan last updated on 02/Oct/21

not really sure sir. i tried but didnt get b−a=14. thats why i posted it on this platform for further conviction from others

$$\:{not}\:{really}\:{sure}\:{sir}.\:{i}\:{tried}\:{but} \\ $$$$\:{didnt}\:{get}\:{b}−{a}=\mathrm{14}.\:{thats}\:{why}\:{i} \\ $$$$\:{posted}\:{it}\:{on}\:{this}\:{platform}\:{for}\:{further} \\ $$$$\:{conviction}\:{from}\:{others} \\ $$

Commented by Rasheed.Sindhi last updated on 03/Oct/21

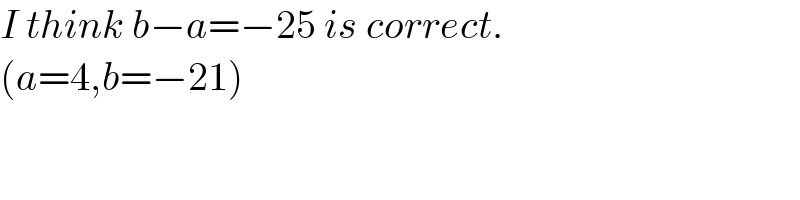
I think b−a=−25 is correct. (a=4,b=−21)

$${I}\:{think}\:{b}−{a}=−\mathrm{25}\:{is}\:{correct}. \\ $$$$\left({a}=\mathrm{4},{b}=−\mathrm{21}\right) \\ $$

Answered by Rasheed.Sindhi last updated on 02/Oct/21

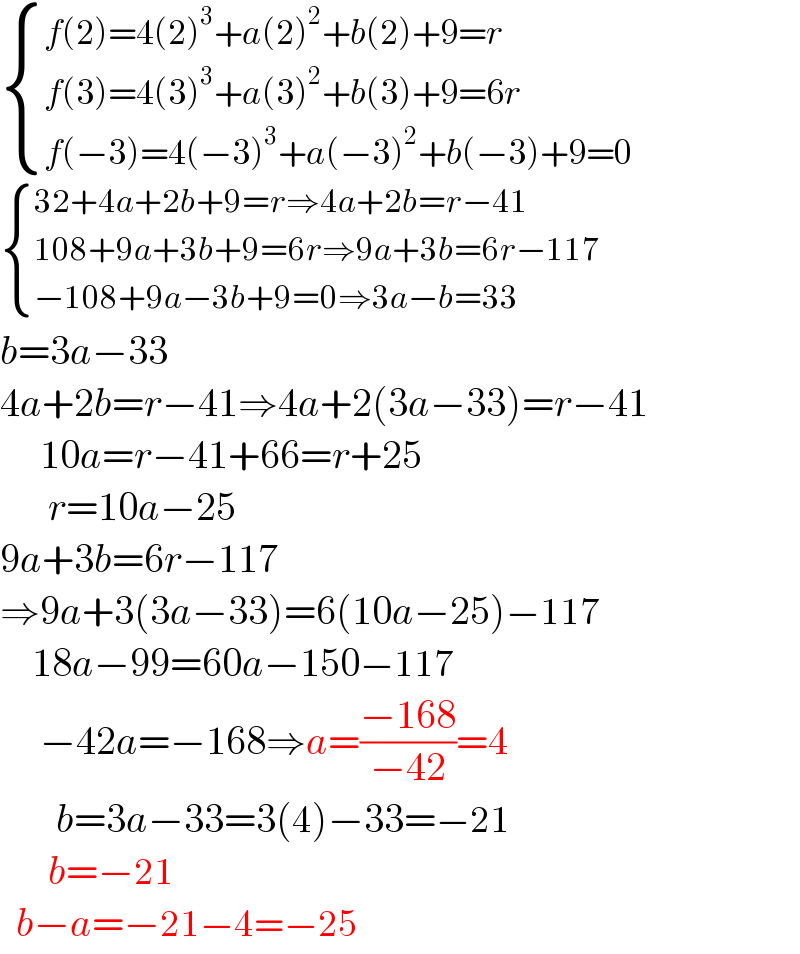
{ ((f(2)=4(2)^3 +a(2)^2 +b(2)+9=r)),((f(3)=4(3)^3 +a(3)^2 +b(3)+9=6r)),((f(−3)=4(−3)^3 +a(−3)^2 +b(−3)+9=0)) :} { ((32+4a+2b+9=r⇒4a+2b=r−41)),((108+9a+3b+9=6r⇒9a+3b=6r−117)),((−108+9a−3b+9=0⇒3a−b=33)) :} b=3a−33 4a+2b=r−41⇒4a+2(3a−33)=r−41 10a=r−41+66=r+25 r=10a−25 9a+3b=6r−117 ⇒9a+3(3a−33)=6(10a−25)−117 18a−99=60a−150−117 −42a=−168⇒a=((−168)/(−42))=4 b=3a−33=3(4)−33=−21 b=−21 b−a=−21−4=−25

$$\begin{cases}{{f}\left(\mathrm{2}\right)=\mathrm{4}\left(\mathrm{2}\right)^{\mathrm{3}} +{a}\left(\mathrm{2}\right)^{\mathrm{2}} +{b}\left(\mathrm{2}\right)+\mathrm{9}={r}}\\{{f}\left(\mathrm{3}\right)=\mathrm{4}\left(\mathrm{3}\right)^{\mathrm{3}} +{a}\left(\mathrm{3}\right)^{\mathrm{2}} +{b}\left(\mathrm{3}\right)+\mathrm{9}=\mathrm{6}{r}}\\{{f}\left(−\mathrm{3}\right)=\mathrm{4}\left(−\mathrm{3}\right)^{\mathrm{3}} +{a}\left(−\mathrm{3}\right)^{\mathrm{2}} +{b}\left(−\mathrm{3}\right)+\mathrm{9}=\mathrm{0}}\end{cases} \\ $$$$\begin{cases}{\mathrm{32}+\mathrm{4}{a}+\mathrm{2}{b}+\mathrm{9}={r}\Rightarrow\mathrm{4}{a}+\mathrm{2}{b}={r}−\mathrm{41}}\\{\mathrm{108}+\mathrm{9}{a}+\mathrm{3}{b}+\mathrm{9}=\mathrm{6}{r}\Rightarrow\mathrm{9}{a}+\mathrm{3}{b}=\mathrm{6}{r}−\mathrm{117}}\\{−\mathrm{108}+\mathrm{9}{a}−\mathrm{3}{b}+\mathrm{9}=\mathrm{0}\Rightarrow\mathrm{3}{a}−{b}=\mathrm{33}}\end{cases} \\ $$$${b}=\mathrm{3}{a}−\mathrm{33} \\ $$$$\mathrm{4}{a}+\mathrm{2}{b}={r}−\mathrm{41}\Rightarrow\mathrm{4}{a}+\mathrm{2}\left(\mathrm{3}{a}−\mathrm{33}\right)={r}−\mathrm{41} \\ $$$$\:\:\:\:\:\mathrm{10}{a}={r}−\mathrm{41}+\mathrm{66}={r}+\mathrm{25} \\ $$$$\:\:\:\:\:\:{r}=\mathrm{10}{a}−\mathrm{25} \\ $$$$\mathrm{9}{a}+\mathrm{3}{b}=\mathrm{6}{r}−\mathrm{117} \\ $$$$\Rightarrow\mathrm{9}{a}+\mathrm{3}\left(\mathrm{3}{a}−\mathrm{33}\right)=\mathrm{6}\left(\mathrm{10}{a}−\mathrm{25}\right)−\mathrm{117} \\ $$$$\:\:\:\:\mathrm{18}{a}−\mathrm{99}=\mathrm{60}{a}−\mathrm{150}−\mathrm{117} \\ $$$$\:\:\:\:\:−\mathrm{42}{a}=−\mathrm{168}\Rightarrow{a}=\frac{−\mathrm{168}}{−\mathrm{42}}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:{b}=\mathrm{3}{a}−\mathrm{33}=\mathrm{3}\left(\mathrm{4}\right)−\mathrm{33}=−\mathrm{21} \\ $$$$\:\:\:\:\:\:{b}=−\mathrm{21} \\ $$$$\:\:{b}−{a}=−\mathrm{21}−\mathrm{4}=−\mathrm{25} \\ $$

Commented by MathsFan last updated on 02/Oct/21

amazing

$${amazing} \\ $$

Answered by Rasheed.Sindhi last updated on 02/Oct/21

determinant (((2)),4,a,b,9),(,,8,(2a+16),(4a+2b+32)),(,4,(a+8),(2a+b+16),(4a+2b+41=r...A))) determinant (((3)),4,a,b,9),(,,(12),(3a+36),(9a+3b+108)),(,4,(a+12),(3a+b+36),(9a+3b+117=6r...B))) determinant (((−3)),4,a,b,9),(,,(−12),(−3a+36),(9a−3b−108)),(,4,(a−12),(−3a+b+36),(9a−3b−99=0...C))) C⇒3a−b=33⇒b=3a−33 B+C: 18a+18=6r⇒r=3a+3 A: 4a+2b+41=r 4a+2(3a−33)+41=3a+3 10a−66+41=3a+3 7a=3+25=28 a=4 b=3a−33=3(4)−33=−21 b−a=−21−4=−25

$$\begin{array}{|c|c|c|}{\left.\mathrm{2}\right)}&\hline{\mathrm{4}}&\hline{{a}}&\hline{{b}}&\hline{\mathrm{9}}\\{}&\hline{}&\hline{\mathrm{8}}&\hline{\mathrm{2}{a}+\mathrm{16}}&\hline{\mathrm{4}{a}+\mathrm{2}{b}+\mathrm{32}}\\{}&\hline{\mathrm{4}}&\hline{{a}+\mathrm{8}}&\hline{\mathrm{2}{a}+{b}+\mathrm{16}}&\hline{\mathrm{4}{a}+\mathrm{2}{b}+\mathrm{41}={r}...{A}}\\\hline\end{array}\: \\ $$$$\begin{array}{|c|c|c|}{\left.\mathrm{3}\right)}&\hline{\mathrm{4}}&\hline{{a}}&\hline{{b}}&\hline{\mathrm{9}}\\{}&\hline{}&\hline{\mathrm{12}}&\hline{\mathrm{3}{a}+\mathrm{36}}&\hline{\mathrm{9}{a}+\mathrm{3}{b}+\mathrm{108}}\\{}&\hline{\mathrm{4}}&\hline{{a}+\mathrm{12}}&\hline{\mathrm{3}{a}+{b}+\mathrm{36}}&\hline{\mathrm{9}{a}+\mathrm{3}{b}+\mathrm{117}=\mathrm{6}{r}...{B}}\\\hline\end{array}\:\: \\ $$$$\begin{array}{|c|c|c|}{\left.−\mathrm{3}\right)}&\hline{\mathrm{4}}&\hline{{a}}&\hline{{b}}&\hline{\mathrm{9}}\\{}&\hline{}&\hline{−\mathrm{12}}&\hline{−\mathrm{3}{a}+\mathrm{36}}&\hline{\mathrm{9}{a}−\mathrm{3}{b}−\mathrm{108}}\\{}&\hline{\mathrm{4}}&\hline{{a}−\mathrm{12}}&\hline{−\mathrm{3}{a}+{b}+\mathrm{36}}&\hline{\mathrm{9}{a}−\mathrm{3}{b}−\mathrm{99}=\mathrm{0}...{C}}\\\hline\end{array}\: \\ $$$${C}\Rightarrow\mathrm{3}{a}−{b}=\mathrm{33}\Rightarrow{b}=\mathrm{3}{a}−\mathrm{33} \\ $$$$\:{B}+{C}:\:\mathrm{18}{a}+\mathrm{18}=\mathrm{6}{r}\Rightarrow{r}=\mathrm{3}{a}+\mathrm{3} \\ $$$${A}:\:\mathrm{4}{a}+\mathrm{2}{b}+\mathrm{41}={r} \\ $$$$\:\:\:\:\:\:\mathrm{4}{a}+\mathrm{2}\left(\mathrm{3}{a}−\mathrm{33}\right)+\mathrm{41}=\mathrm{3}{a}+\mathrm{3} \\ $$$$\:\:\:\:\:\:\mathrm{10}{a}−\mathrm{66}+\mathrm{41}=\mathrm{3}{a}+\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\mathrm{7}{a}=\mathrm{3}+\mathrm{25}=\mathrm{28} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:{b}=\mathrm{3}{a}−\mathrm{33}=\mathrm{3}\left(\mathrm{4}\right)−\mathrm{33}=−\mathrm{21} \\ $$$${b}−{a}=−\mathrm{21}−\mathrm{4}=−\mathrm{25} \\ $$

Commented by MathsFan last updated on 02/Oct/21

thank you sir but which approach is this

$${thank}\:{you}\:{sir} \\ $$$$\:{but}\:{which}\:{approach}\:{is}\:{this} \\ $$

Commented by Rasheed.Sindhi last updated on 02/Oct/21

This is synthetic division approach

$$\mathcal{T}{his}\:{is}\:\:{synthetic}\:{division}\:{approach} \\ $$

Commented by peter frank last updated on 02/Oct/21

thanks

$$\mathrm{thanks} \\ $$

Commented by Tawa11 last updated on 03/Oct/21

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by Rasheed.Sindhi last updated on 03/Oct/21

You are certainly miss tawa,an old forum-friend ?

$${You}\:{are}\:{certainly}\:{miss}\:{tawa},{an} \\ $$$${old}\:{forum}-{friend}\:? \\ $$

Answered by Rasheed.Sindhi last updated on 03/Oct/21

Verification : a=4,b=−21 f(x)=4x^3 +4x^2 −21x+9 •When divided by x−2 f(2)=4(2)^3 +4(2)^2 −21(2)+9=r =32+16−42+9=15=r •When divided by x−3 f(3)=4(3)^3 +4(3)^2 −21(3)+9=6r =108+36−63+9=90=6×15=6r • x+3 is factor of f(x) determinant (((−3)),4,( 4),(−21),( 9)),(,,(−12),( 24),(−9)),(,4,( −8),( 3),( 0))) 4x^3 +4x^2 −21x+9 =(x+3)(4x^2 −8x+3) V e r i f i e d

$$\mathrm{Verification}\:: \\ $$$${a}=\mathrm{4},{b}=−\mathrm{21} \\ $$$${f}\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{9} \\ $$$$\bullet{When}\:{divided}\:{by}\:{x}−\mathrm{2} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{4}\left(\mathrm{2}\right)^{\mathrm{3}} +\mathrm{4}\left(\mathrm{2}\right)^{\mathrm{2}} −\mathrm{21}\left(\mathrm{2}\right)+\mathrm{9}={r} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{32}+\mathrm{16}−\mathrm{42}+\mathrm{9}=\mathrm{15}={r} \\ $$$$\bullet{When}\:{divided}\:{by}\:{x}−\mathrm{3} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{4}\left(\mathrm{3}\right)^{\mathrm{3}} +\mathrm{4}\left(\mathrm{3}\right)^{\mathrm{2}} −\mathrm{21}\left(\mathrm{3}\right)+\mathrm{9}=\mathrm{6}{r} \\ $$$$\:\:\:\:\:=\mathrm{108}+\mathrm{36}−\mathrm{63}+\mathrm{9}=\mathrm{90}=\mathrm{6}×\mathrm{15}=\mathrm{6}{r} \\ $$$$\bullet\:{x}+\mathrm{3}\:{is}\:{factor}\:{of}\:{f}\left({x}\right) \\ $$$$\begin{array}{|c|c|c|}{\left.−\mathrm{3}\right)}&\hline{\mathrm{4}}&\hline{\:\:\:\:\:\mathrm{4}}&\hline{−\mathrm{21}}&\hline{\:\:\:\mathrm{9}}\\{}&\hline{}&\hline{−\mathrm{12}}&\hline{\:\:\:\mathrm{24}}&\hline{−\mathrm{9}}\\{}&\hline{\mathrm{4}}&\hline{\:\:−\mathrm{8}}&\hline{\:\:\:\:\mathrm{3}}&\hline{\:\:\mathrm{0}}\\\hline\end{array}\: \\ $$$$\mathrm{4}{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{21}{x}+\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left({x}+\mathrm{3}\right)\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{3}\right) \\ $$$$\mathrm{V}\:\mathrm{e}\:\mathrm{r}\:\mathrm{i}\:\mathrm{f}\:\mathrm{i}\:\mathrm{e}\:\mathrm{d} \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 04/Oct/21

AnOther Way ^• x+3 is factor of 4x^3 +ax^2 +bx+9. Let other factor is 4x^2 +px+3 ∴ f(x)=(x+3)(4x^2 +px+3) =4x^3 +(p+12)x^2 +(3p+3)x+9 Comparing coefficients a=p+12⇒p=a−12, b=3p+3=3(a−12)+3=3a−33 ∴ f(x)=4x^3 +ax^2 +(3a−33)x+9 ^• f(x) divided by x−2 leaving remainder r f(2)=4(2)^3 +a(2)^2 +(3a−33)(2)+9=r =32+4a+6a−66+9=r 10a−25=r ^• f(x) divided by x−3 leaving remainder 6r f(3)=4(3)^3 +a(3)^2 +(3a−33)(3)+9=6r =108+9a+9a−99+9=6(10a−25) 18a+18=60a−150 42a=168⇒a=4 b=3a−33=3(4)−33=−21 b=−21 b−a=−21−4=−25

$$\mathbb{A}\mathrm{n}\mathbb{O}\mathrm{ther}\:\mathbb{W}\mathrm{ay} \\ $$$$\:^{\bullet} {x}+\mathrm{3}\:\mathrm{is}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{4}{x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +{bx}+\mathrm{9}. \\ $$$${Let}\:{other}\:{factor}\:{is}\:\mathrm{4}{x}^{\mathrm{2}} +{px}+\mathrm{3} \\ $$$$\therefore\:{f}\left({x}\right)=\left({x}+\mathrm{3}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +{px}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{4}{x}^{\mathrm{3}} +\left({p}+\mathrm{12}\right){x}^{\mathrm{2}} +\left(\mathrm{3}{p}+\mathrm{3}\right){x}+\mathrm{9} \\ $$$${Comparing}\:{coefficients} \\ $$$${a}={p}+\mathrm{12}\Rightarrow{p}={a}−\mathrm{12}, \\ $$$${b}=\mathrm{3}{p}+\mathrm{3}=\mathrm{3}\left({a}−\mathrm{12}\right)+\mathrm{3}=\mathrm{3}{a}−\mathrm{33} \\ $$$$\therefore\:{f}\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} +{ax}^{\mathrm{2}} +\left(\mathrm{3}{a}−\mathrm{33}\right){x}+\mathrm{9} \\ $$$$\:^{\bullet} {f}\left({x}\right)\:{divided}\:{by}\:{x}−\mathrm{2}\:{leaving}\: \\ $$$${remainder}\:{r} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{4}\left(\mathrm{2}\right)^{\mathrm{3}} +{a}\left(\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{3}{a}−\mathrm{33}\right)\left(\mathrm{2}\right)+\mathrm{9}={r} \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{32}+\mathrm{4}{a}+\mathrm{6}{a}−\mathrm{66}+\mathrm{9}={r} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{10}{a}−\mathrm{25}={r} \\ $$$$\:^{\bullet} {f}\left({x}\right)\:{divided}\:{by}\:{x}−\mathrm{3}\:{leaving}\: \\ $$$${remainder}\:\mathrm{6}{r} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{4}\left(\mathrm{3}\right)^{\mathrm{3}} +{a}\left(\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{3}{a}−\mathrm{33}\right)\left(\mathrm{3}\right)+\mathrm{9}=\mathrm{6}{r} \\ $$$$\:\:\:\:\:=\mathrm{108}+\mathrm{9}{a}+\mathrm{9}{a}−\mathrm{99}+\mathrm{9}=\mathrm{6}\left(\mathrm{10}{a}−\mathrm{25}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{18}{a}+\mathrm{18}=\mathrm{60}{a}−\mathrm{150} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{42}{a}=\mathrm{168}\Rightarrow{a}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\:\:\:{b}=\mathrm{3}{a}−\mathrm{33}=\mathrm{3}\left(\mathrm{4}\right)−\mathrm{33}=−\mathrm{21} \\ $$$$\:\:\:\:\:\:\:\:\:\:{b}=−\mathrm{21} \\ $$$$\:\:\:\:\:\:\:\:\:{b}−{a}=−\mathrm{21}−\mathrm{4}=−\mathrm{25} \\ $$

Answered by ajfour last updated on 03/Oct/21

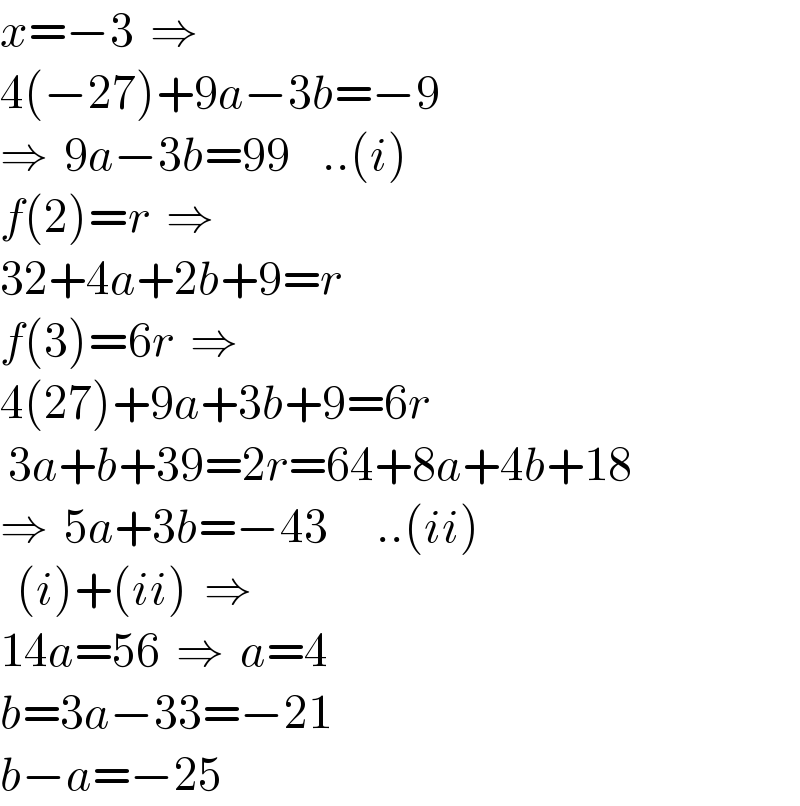
x=−3 ⇒ 4(−27)+9a−3b=−9 ⇒ 9a−3b=99 ..(i) f(2)=r ⇒ 32+4a+2b+9=r f(3)=6r ⇒ 4(27)+9a+3b+9=6r 3a+b+39=2r=64+8a+4b+18 ⇒ 5a+3b=−43 ..(ii) (i)+(ii) ⇒ 14a=56 ⇒ a=4 b=3a−33=−21 b−a=−25

$${x}=−\mathrm{3}\:\:\Rightarrow \\ $$$$\mathrm{4}\left(−\mathrm{27}\right)+\mathrm{9}{a}−\mathrm{3}{b}=−\mathrm{9} \\ $$$$\Rightarrow\:\:\mathrm{9}{a}−\mathrm{3}{b}=\mathrm{99}\:\:\:\:..\left({i}\right) \\ $$$${f}\left(\mathrm{2}\right)={r}\:\:\Rightarrow \\ $$$$\mathrm{32}+\mathrm{4}{a}+\mathrm{2}{b}+\mathrm{9}={r} \\ $$$${f}\left(\mathrm{3}\right)=\mathrm{6}{r}\:\:\Rightarrow \\ $$$$\mathrm{4}\left(\mathrm{27}\right)+\mathrm{9}{a}+\mathrm{3}{b}+\mathrm{9}=\mathrm{6}{r} \\ $$$$\:\mathrm{3}{a}+{b}+\mathrm{39}=\mathrm{2}{r}=\mathrm{64}+\mathrm{8}{a}+\mathrm{4}{b}+\mathrm{18} \\ $$$$\Rightarrow\:\:\mathrm{5}{a}+\mathrm{3}{b}=−\mathrm{43}\:\:\:\:\:\:..\left({ii}\right) \\ $$$$\:\:\left({i}\right)+\left({ii}\right)\:\:\Rightarrow \\ $$$$\mathrm{14}{a}=\mathrm{56}\:\:\Rightarrow\:\:{a}=\mathrm{4} \\ $$$${b}=\mathrm{3}{a}−\mathrm{33}=−\mathrm{21} \\ $$$${b}−{a}=−\mathrm{25} \\ $$

Answered by Rasheed.Sindhi last updated on 04/Oct/21

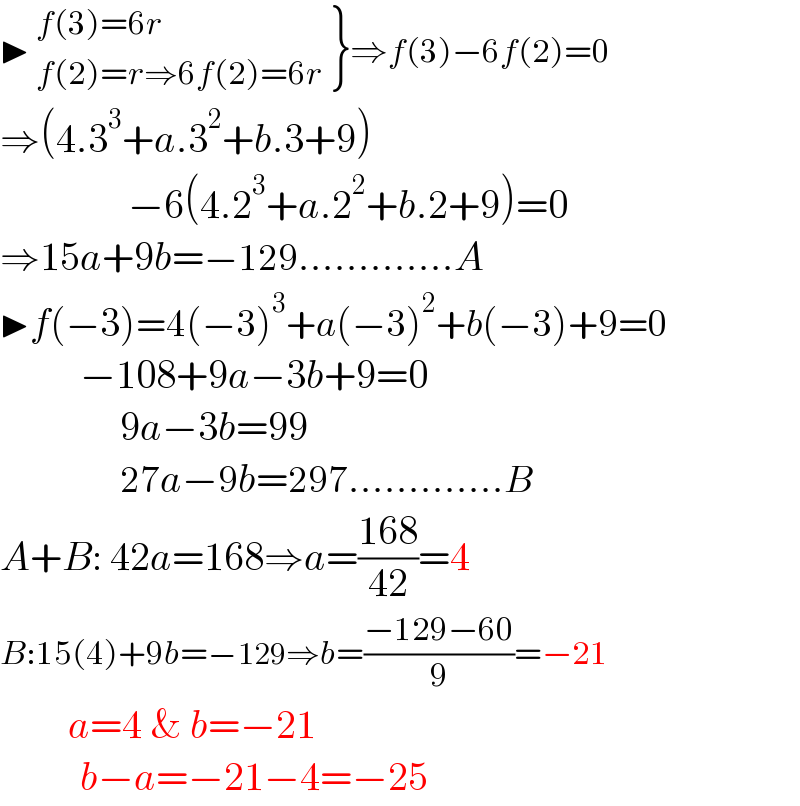
▶ {: ((f(3)=6r)),((f(2)=r⇒6f(2)=6r)) }⇒f(3)−6f(2)=0 ⇒(4.3^3 +a.3^2 +b.3+9) −6(4.2^3 +a.2^2 +b.2+9)=0 ⇒15a+9b=−129.............A ▶f(−3)=4(−3)^3 +a(−3)^2 +b(−3)+9=0 −108+9a−3b+9=0 9a−3b=99 27a−9b=297.............B A+B: 42a=168⇒a=((168)/(42))=4 B:15(4)+9b=−129⇒b=((−129−60)/9)=−21 a=4 & b=−21 b−a=−21−4=−25

$$\blacktriangleright\:\left.\begin{matrix}{{f}\left(\mathrm{3}\right)=\mathrm{6}{r}}\\{{f}\left(\mathrm{2}\right)={r}\Rightarrow\mathrm{6}{f}\left(\mathrm{2}\right)=\mathrm{6}{r}}\end{matrix}\right\}\Rightarrow{f}\left(\mathrm{3}\right)−\mathrm{6}{f}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{4}.\mathrm{3}^{\mathrm{3}} +{a}.\mathrm{3}^{\mathrm{2}} +{b}.\mathrm{3}+\mathrm{9}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6}\left(\mathrm{4}.\mathrm{2}^{\mathrm{3}} +{a}.\mathrm{2}^{\mathrm{2}} +{b}.\mathrm{2}+\mathrm{9}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{15}{a}+\mathrm{9}{b}=−\mathrm{129}.............{A} \\ $$$$\blacktriangleright{f}\left(−\mathrm{3}\right)=\mathrm{4}\left(−\mathrm{3}\right)^{\mathrm{3}} +{a}\left(−\mathrm{3}\right)^{\mathrm{2}} +{b}\left(−\mathrm{3}\right)+\mathrm{9}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:−\mathrm{108}+\mathrm{9}{a}−\mathrm{3}{b}+\mathrm{9}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}{a}−\mathrm{3}{b}=\mathrm{99} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{27}{a}−\mathrm{9}{b}=\mathrm{297}.............{B} \\ $$$${A}+{B}:\:\mathrm{42}{a}=\mathrm{168}\Rightarrow{a}=\frac{\mathrm{168}}{\mathrm{42}}=\mathrm{4} \\ $$$${B}:\mathrm{15}\left(\mathrm{4}\right)+\mathrm{9}{b}=−\mathrm{129}\Rightarrow{b}=\frac{−\mathrm{129}−\mathrm{60}}{\mathrm{9}}=−\mathrm{21} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{a}=\mathrm{4}\:\&\:{b}=−\mathrm{21} \\ $$$$\:\:\:\:\:\:\:\:\:\:{b}−{a}=−\mathrm{21}−\mathrm{4}=−\mathrm{25} \\ $$

Answered by Rasheed.Sindhi last updated on 04/Oct/21

f(3)=6r_(A) ∧ f(2)=r_(B) (A/B) ⇒ ((f(3))/(f(2)))=6⇒f(3)−6f(2)=0 ⇒4.3^3 +a.3^2 +b.3+9−6(4.2^3 +a.2^2 +b.2+9)=0 ⇒4.3^3 +a.3^2 +b.3+9−24.2^3 −6a.2^2 −6b.2−54=0 ⇒108+9a+3b+9−192−24a−12b−54=0 −15a−9b=129 5a+3b=−43...............(i) ▶f(−3)=4(−3)^3 +a(−3)^2 +b(−3)+9=0 ⇒−108+9a−3b+9=0 ⇒3a−b=33................(ii) (i) & (ii): a=4,b=−21 b−a=−21−4=−25

$$\underset{{A}} {\underbrace{{f}\left(\mathrm{3}\right)=\mathrm{6}{r}}}\:\wedge\:\underset{{B}} {\underbrace{{f}\left(\mathrm{2}\right)={r}}} \\ $$$$\:\frac{{A}}{{B}}\:\Rightarrow\:\:\:\frac{{f}\left(\mathrm{3}\right)}{{f}\left(\mathrm{2}\right)}=\mathrm{6}\Rightarrow{f}\left(\mathrm{3}\right)−\mathrm{6}{f}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}.\mathrm{3}^{\mathrm{3}} +{a}.\mathrm{3}^{\mathrm{2}} +{b}.\mathrm{3}+\mathrm{9}−\mathrm{6}\left(\mathrm{4}.\mathrm{2}^{\mathrm{3}} +{a}.\mathrm{2}^{\mathrm{2}} +{b}.\mathrm{2}+\mathrm{9}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}.\mathrm{3}^{\mathrm{3}} +{a}.\mathrm{3}^{\mathrm{2}} +{b}.\mathrm{3}+\mathrm{9}−\mathrm{24}.\mathrm{2}^{\mathrm{3}} −\mathrm{6}{a}.\mathrm{2}^{\mathrm{2}} −\mathrm{6}{b}.\mathrm{2}−\mathrm{54}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{108}+\mathrm{9}{a}+\mathrm{3}{b}+\mathrm{9}−\mathrm{192}−\mathrm{24}{a}−\mathrm{12}{b}−\mathrm{54}=\mathrm{0} \\ $$$$\:\:\:−\mathrm{15}{a}−\mathrm{9}{b}=\mathrm{129} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{5}{a}+\mathrm{3}{b}=−\mathrm{43}...............\left({i}\right) \\ $$$$\blacktriangleright{f}\left(−\mathrm{3}\right)=\mathrm{4}\left(−\mathrm{3}\right)^{\mathrm{3}} +{a}\left(−\mathrm{3}\right)^{\mathrm{2}} +{b}\left(−\mathrm{3}\right)+\mathrm{9}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow−\mathrm{108}+\mathrm{9}{a}−\mathrm{3}{b}+\mathrm{9}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\mathrm{3}{a}−{b}=\mathrm{33}................\left({ii}\right) \\ $$$$\left({i}\right)\:\&\:\left({ii}\right):\:\:\:{a}=\mathrm{4},{b}=−\mathrm{21} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}−{a}=−\mathrm{21}−\mathrm{4}=−\mathrm{25} \\ $$$$\:\:\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com