
Question and Answers Forum
Question Number 15558 by ajfour last updated on 11/Jun/17
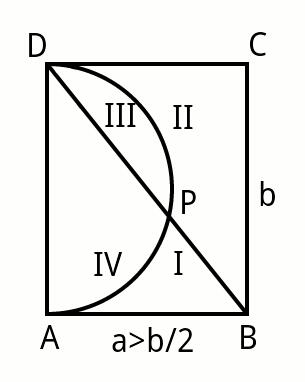
Commented by ajfour last updated on 11/Jun/17
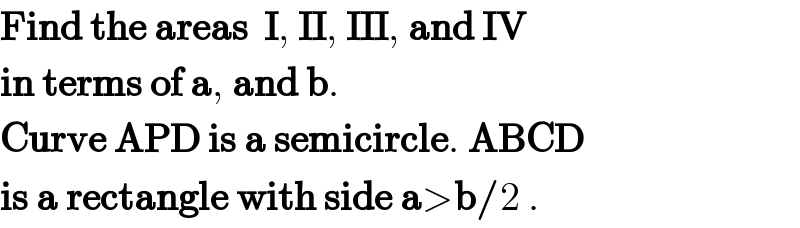
Answered by mrW1 last updated on 11/Jun/17
![α=tan^(−1) (a/b) ∠DOP=π−2α A_(III) =(1/2)((b/2))^2 [π−2α−sin (π−2α)] =(b^2 /8)[π−2α−sin 2α] =(b^2 /8)[π−2α−2×((ab)/(a^2 +b^2 ))] =(b^2 /4)[(π/2)−tan^(−1) (a/b)−((ab)/(a^2 +b^2 ))] A_(IV) =(π/2)((b/2))^2 −A_(III) =(b^2 /4)[tan^(−1) (a/b)+((ab)/(a^2 +b^2 ))] A_(II) =((ab)/2)−A_(III) =((ab)/2)−(b^2 /4)[(π/2)−tan^(−1) (a/b)−((ab)/(a^2 +b^2 ))] A_I =((ab)/2)−A_(IV) =((ab)/2)−(b^2 /4)[tan^(−1) (a/b)+((ab)/(a^2 +b^2 ))]](Q15563.png)
Commented by mrW1 last updated on 11/Jun/17
| ||
Question and Answers Forum | ||
Question Number 15558 by ajfour last updated on 11/Jun/17 | ||
 | ||
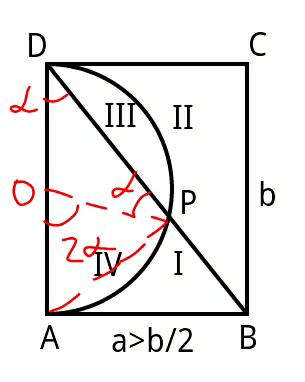
Commented by ajfour last updated on 11/Jun/17 | ||
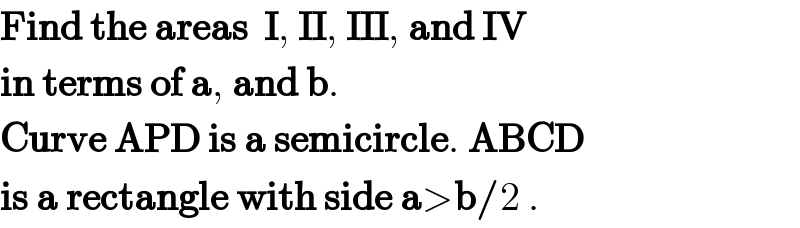 | ||
Answered by mrW1 last updated on 11/Jun/17 | ||
![α=tan^(−1) (a/b) ∠DOP=π−2α A_(III) =(1/2)((b/2))^2 [π−2α−sin (π−2α)] =(b^2 /8)[π−2α−sin 2α] =(b^2 /8)[π−2α−2×((ab)/(a^2 +b^2 ))] =(b^2 /4)[(π/2)−tan^(−1) (a/b)−((ab)/(a^2 +b^2 ))] A_(IV) =(π/2)((b/2))^2 −A_(III) =(b^2 /4)[tan^(−1) (a/b)+((ab)/(a^2 +b^2 ))] A_(II) =((ab)/2)−A_(III) =((ab)/2)−(b^2 /4)[(π/2)−tan^(−1) (a/b)−((ab)/(a^2 +b^2 ))] A_I =((ab)/2)−A_(IV) =((ab)/2)−(b^2 /4)[tan^(−1) (a/b)+((ab)/(a^2 +b^2 ))]](Q15563.png) | ||
| ||
Commented by mrW1 last updated on 11/Jun/17 | ||
 | ||