Question and Answers Forum
Question Number 86313 by john santu last updated on 28/Mar/20
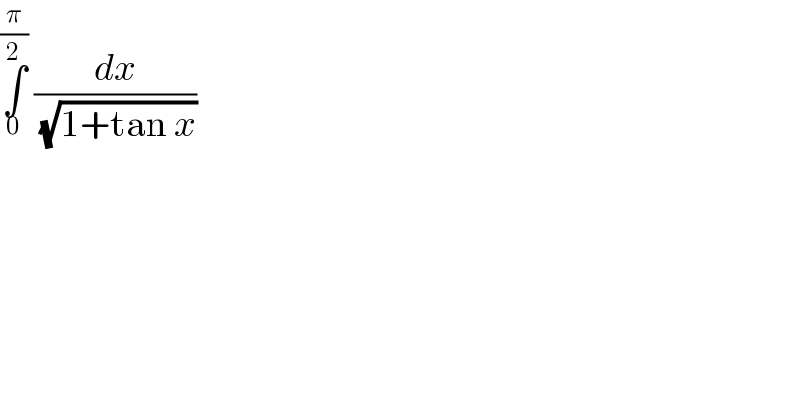
Commented by john santu last updated on 28/Mar/20
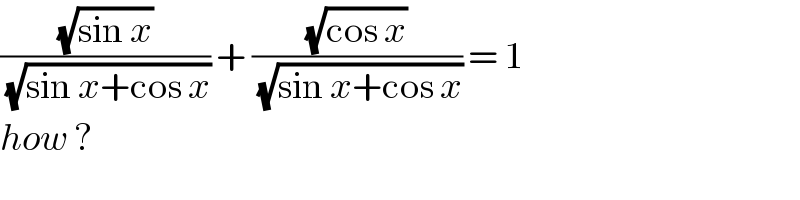
Commented by john santu last updated on 28/Mar/20
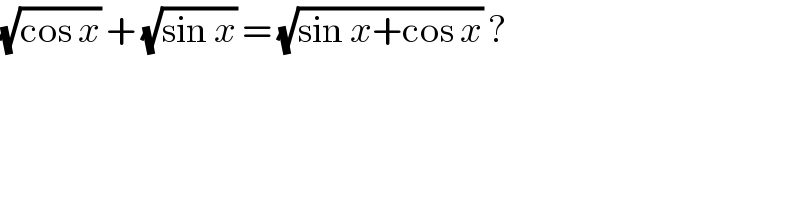
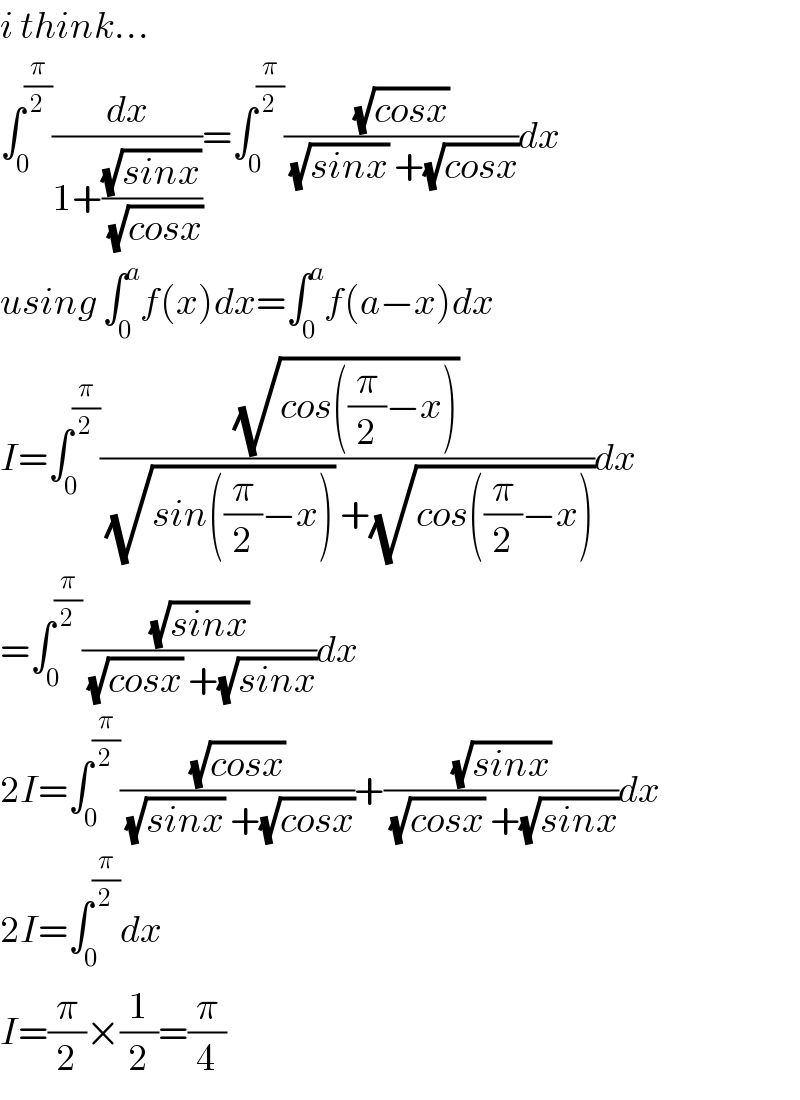
Answered by TANMAY PANACEA. last updated on 28/Mar/20
Commented by jagoll last updated on 28/Mar/20

Commented by TANMAY PANACEA. last updated on 28/Mar/20

Commented by john santu last updated on 28/Mar/20

Commented by TawaTawa1 last updated on 28/Mar/20
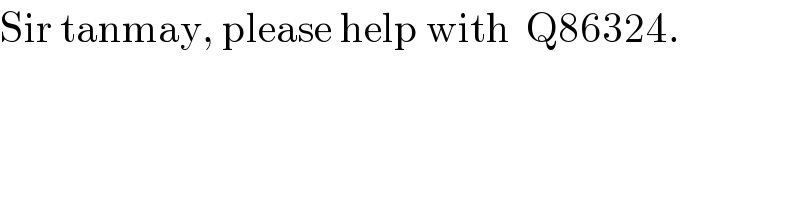
Answered by MJS last updated on 28/Mar/20
![∫(dx/(√(1+tan x)))= [t=(√(1+tan x)) → dx=2cos^2 x (√(1+tan x))dt] =2∫(dt/(t^4 −2t^2 +2)) and now it′s easy](Q86376.png)
Commented by jagoll last updated on 28/Mar/20
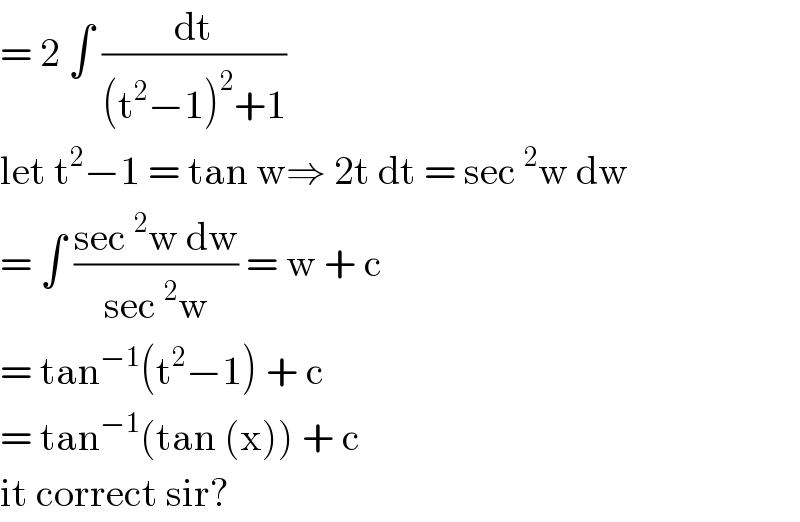
Commented by MJS last updated on 28/Mar/20
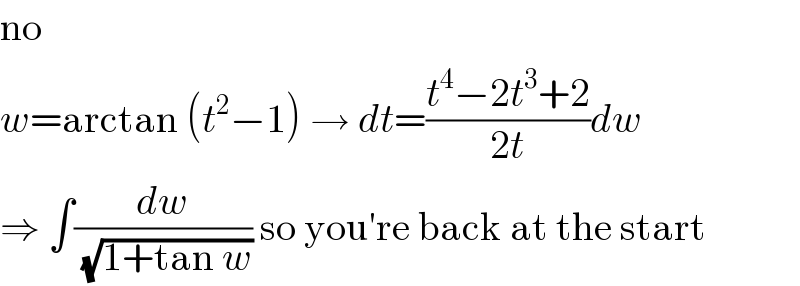
Commented by MJS last updated on 28/Mar/20
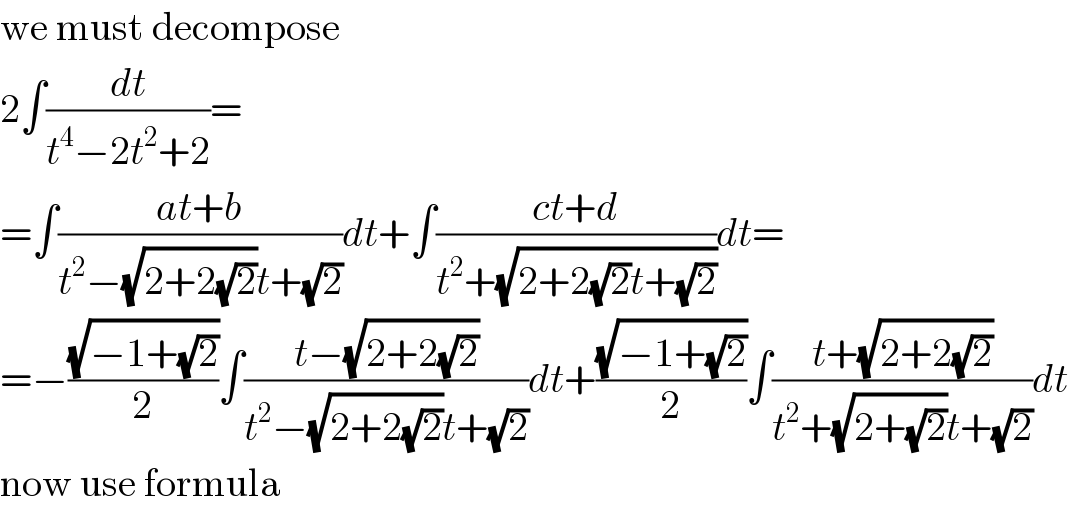
Commented by jagoll last updated on 28/Mar/20