lim_(x−oo) (1/(n(√n))) Σ_(k=1) ^n E((√(k)))


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 155710 by SANOGO last updated on 03/Oct/21

$li \underset{x - o o}{m} \frac{1}{n \sqrt{n}} \underset{k = 1}{\sum^{n}} E (\sqrt{k)}$
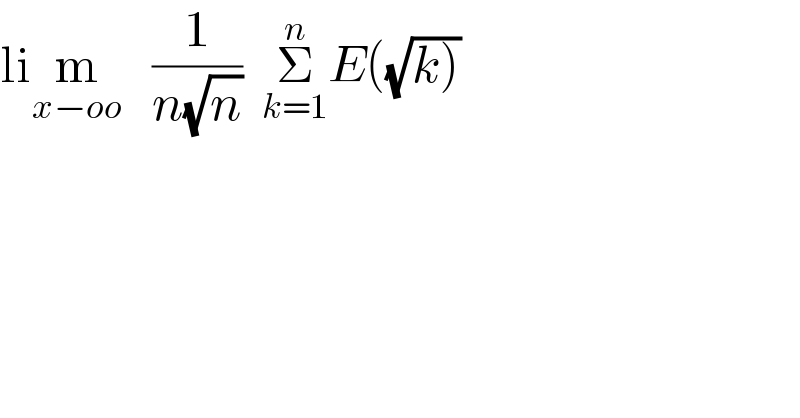
Commented by yeti123 last updated on 03/Oct/21

$\lim_{x \to \infty} \frac{1}{n \sqrt{n}} \underset{k = 1}{\sum^{n}} E (\sqrt{k}) = \frac{1}{n \sqrt{n}} \underset{k = 1}{\sum^{n}} E (\sqrt{k})$
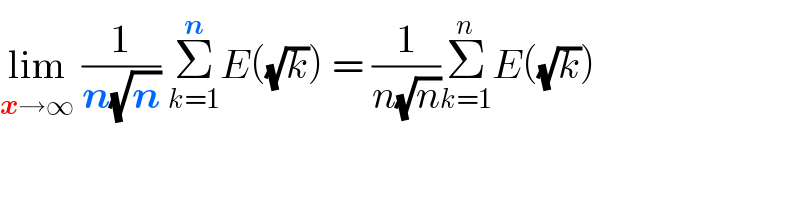
	Answered by puissant last updated on 03/Oct/21

	$L = \lim_{n \to + \infty} \frac{1}{n \sqrt{n}} \underset{k = 1}{\sum^{n}} E (\sqrt{k})$ $L = \lim_{n \to + \infty} \frac{1}{n} \underset{k = 1}{\sum^{n}} \frac{1}{\sqrt{n}} E (\sqrt{k})$ $= \lim_{n \to + \infty} \frac{1}{n} \underset{k = 1}{\sum^{n}} E (\sqrt{\frac{k}{n}})$ $Q u i e s t s o u s l a f o r m e \frac{b - a}{n} \underset{k = 1}{\sum^{n}} f (a + k \frac{b - a}{n})$ $i l s^{'} a g i t d e l a s o m m e d e r i e m a n n o n a d o n c :$ $\lim_{n \to + \infty} \frac{b - a}{n} \underset{k = 1}{\sum^{n}} f (a + k \frac{b - a}{n}) = \int_{a}^{b} f (x) d x$ $\Rightarrow L = \int_{0}^{1} E (x) d x = 0 (1 - 0) = 0 . .$ $∴∵ L = \lim_{n \to + \infty} \frac{1}{n \sqrt{n}} \underset{k = 1}{\sum^{n}} E (\sqrt{k}) = 0 . .$ $. . . . . . . . . . . L e p u i s s a n t . . . . . . . . . . .$
	Commented by SANOGO last updated on 03/Oct/21

	$m e r c i b i e n m o n f r e r e$
	Commented by Kamel last updated on 04/Oct/21

	$M r . P u i s s a n t y E (x) \neq E (x y)$
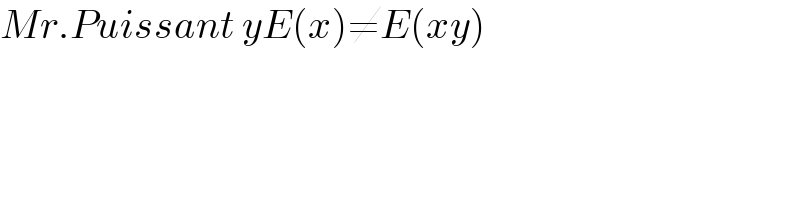
	Commented by puissant last updated on 04/Oct/21

	$T h a n k s M r K a m e l . .$ $M r S a n o g o D e s o l \overset{´}{e e} . .$
	Answered by Kamel last updated on 04/Oct/21
	$S_n =Σ_(k=1) ^n [(√k)]=Σ_(k=1) ^n (√k)−Σ_(k=1) ^n {(√k)} ∀1≤k≤n 0≤ Σ_(k=1) ^n {(√k)}<n ⇒0≤(1/( n(√n)))Σ_(k=1) ^n {(√k)}<(1/( (√n))) ∴ lim_(n→+∞) (1/(n(√n)))Σ_(k=1) ^n [(√k)]=lim_(n→+∞) (1/n)Σ_(k=1) ^n (√(k/n))=∫_0 ^1 (√x)dx =(2/3)$
	$S_{n} = \underset{k = 1}{\sum^{n}} [\sqrt{k}] = \underset{k = 1}{\sum^{n}} \sqrt{k} - \underset{k = 1}{\sum^{n}} {\sqrt{k}}$ $\forall 1 ⩽ k ⩽ n 0 ⩽ \underset{k = 1}{\sum^{n}} {\sqrt{k}} < n \Rightarrow 0 ⩽ \frac{1}{n \sqrt{n}} \underset{k = 1}{\sum^{n}} {\sqrt{k}} < \frac{1}{\sqrt{n}}$ $∴ \underset{n \to + \infty}{l i m} \frac{1}{n \sqrt{n}} \underset{k = 1}{\sum^{n}} [\sqrt{k}] = \underset{n \to + \infty}{l i m} \frac{1}{n} \underset{k = 1}{\sum^{n}} \sqrt{\frac{k}{n}} = \int_{0}^{1} \sqrt{x} d x$ $= \frac{2}{3}$
	Commented by SANOGO last updated on 04/Oct/21

	$merci bien$
	Answered by mindispower last updated on 04/Oct/21

	$x - 1 < E (x) ⩽ x$ $\Rightarrow Σ \frac{1}{n \sqrt{n}} (\sqrt{k} - 1) ⩽ \underset{k = 1}{\sum^{n}} \frac{E (\sqrt{k})}{n \sqrt{n}} < \underset{k = 1}{\sum^{n}} \frac{1}{n \sqrt{n}} \sqrt{k})$ $Σ \frac{1}{n} \sqrt{\frac{k}{n}} - \frac{1}{\sqrt{n}} ⩽ S ⩽ \int_{0}^{1} \sqrt{x} d x$ $\int_{0}^{1} \sqrt{x} d x - \lim_{n \to \infty} \frac{1}{\sqrt{n}} ⩽ S ⩽ \int_{0}^{1} \sqrt{x} d x$ $\frac{3}{2} ⩽ S ⩽ \frac{3}{2}$
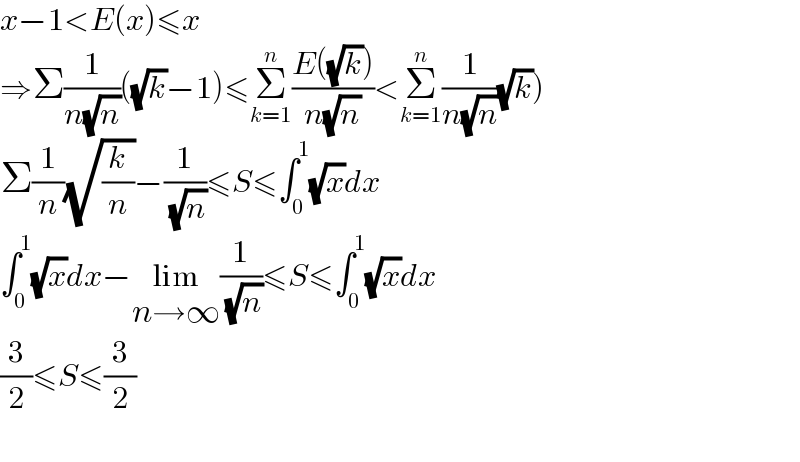
	Commented by SANOGO last updated on 04/Oct/21

	$m e r c i b i e n$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum