
Question and Answers Forum
Question Number 155720 by ajfour last updated on 03/Oct/21
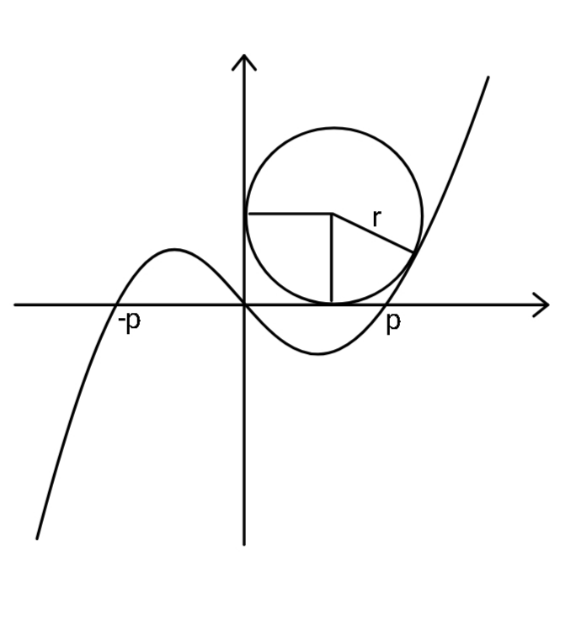
Commented by ajfour last updated on 03/Oct/21
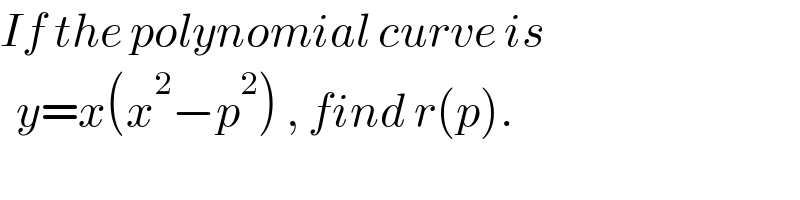
Answered by TheSupreme last updated on 03/Oct/21
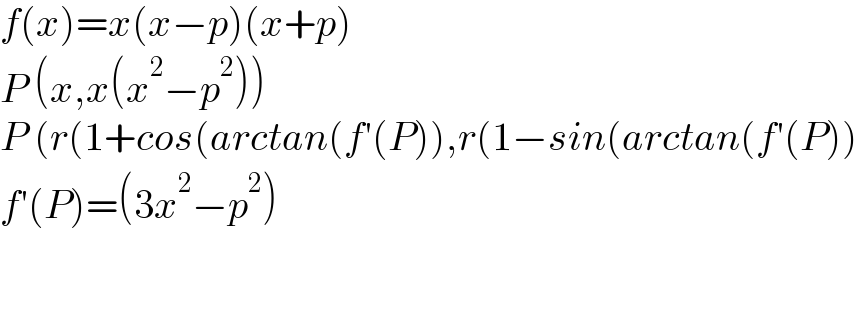
Answered by mr W last updated on 03/Oct/21
![touching point A(a,b) with b=a(a^2 −p^2 ) tan θ=y′=3x^2 −p^2 =3a^2 −p^2 a=r(1+sin θ) b=r(1−cos θ) (b/a)=((1−cos θ)/(1+sin θ)) a^2 −p^2 =((1−cos θ)/(1+sin θ)) ⇒tan θ−((3(1−cos θ))/(1+sin θ))=2p^2 { ((p=(√((1/2)[tan θ−((3(1−cos θ))/(1+sin θ))])))),((r=(1/(1+sin θ))(√((1/2)[tan θ−((1−cos θ)/(1+sin θ))])))) :}](Q155725.png)
Commented by mr W last updated on 03/Oct/21
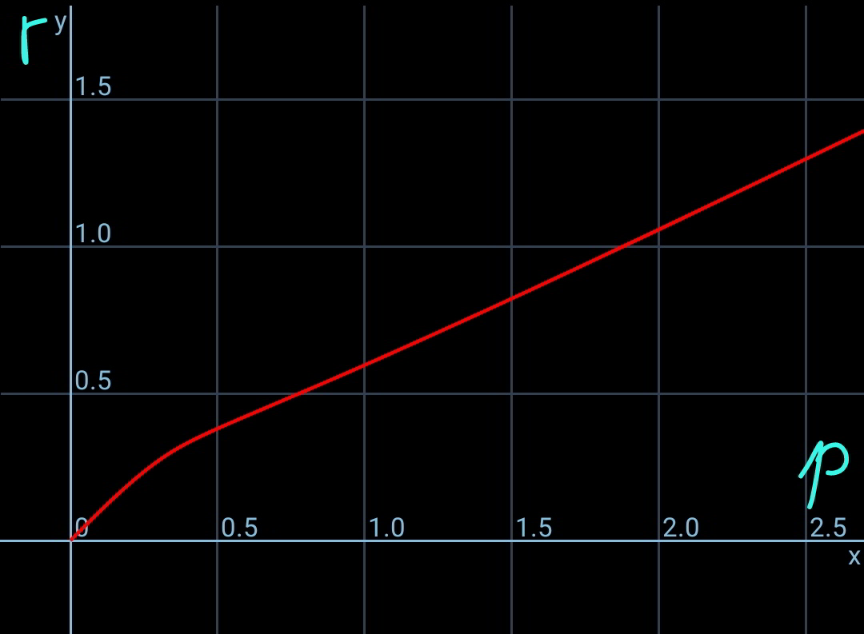
Commented by mr W last updated on 03/Oct/21
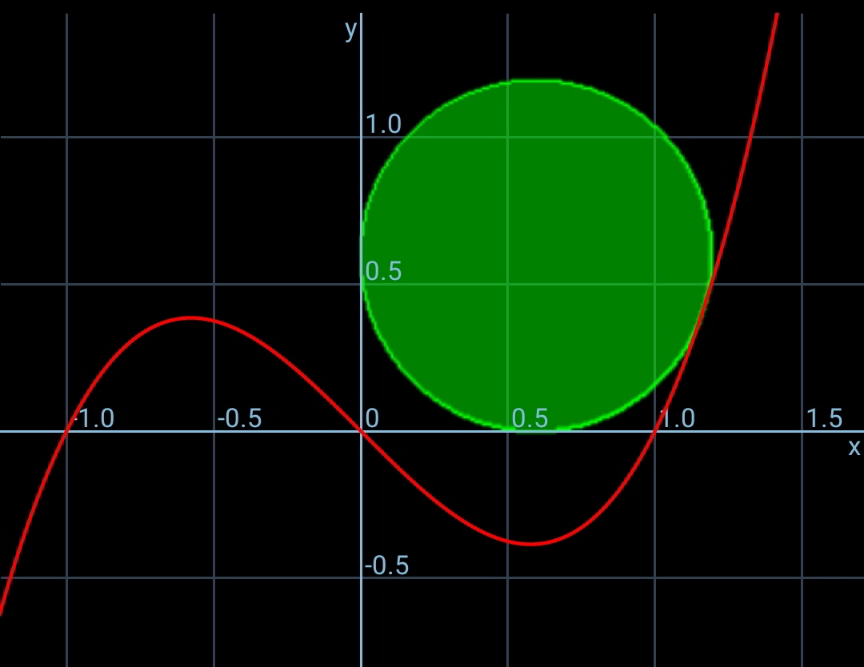
Commented by mr W last updated on 03/Oct/21
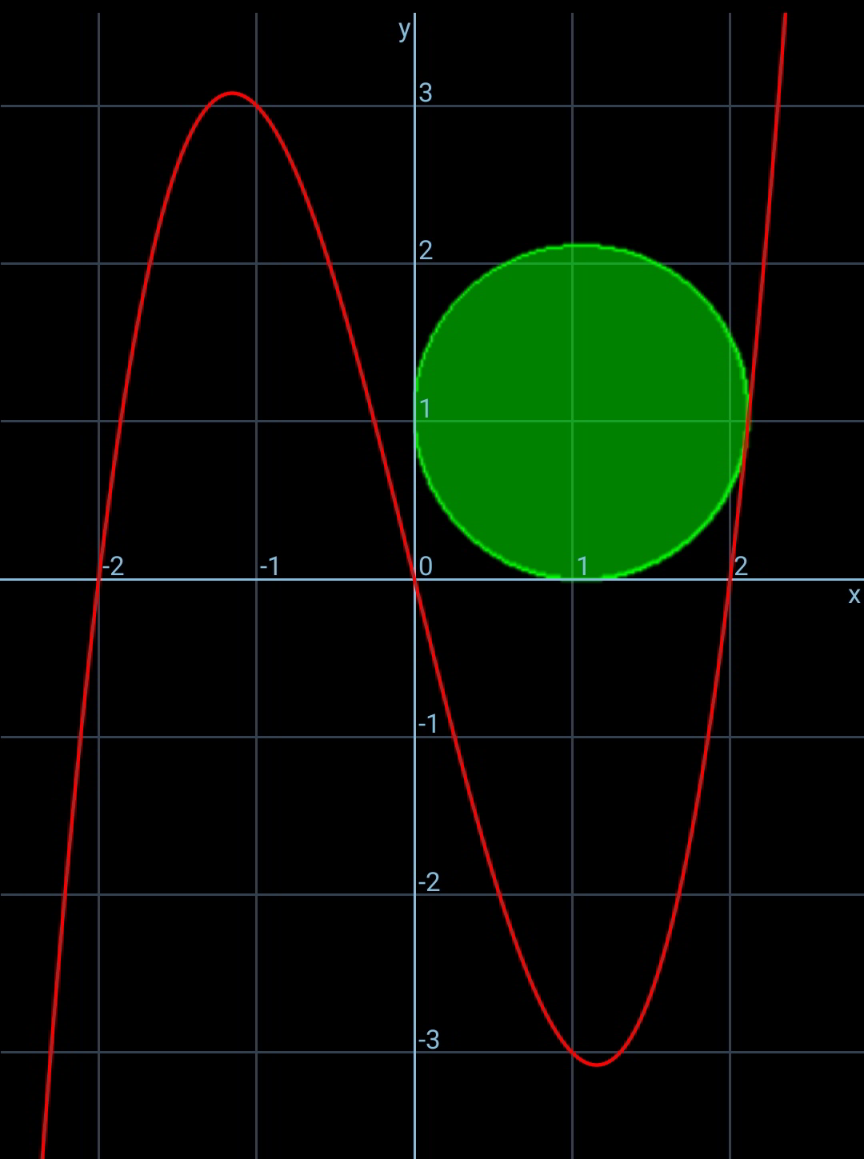
Answered by ajfour last updated on 01/Nov/21
![x=r+rcos θ y=c=r−rsin θ ; p=1 ⇒ c=r(1−2sin φcos φ) 2φ=90°−θ ⇒ r(1−cos 2φ)=x(x^2 −p^2 ) r(1+cos θ)=x 2rsin^2 ((π/4)−(θ/2))=2rcos^2 (θ/2)(4r^2 cos^4 (θ/2)−p^2 ) say (θ/2)=δ (cos δ−sin δ)^2 =cos^2 δ(4r^2 cos^4 δ−p^2 ) ⇒ 2(1−sin θ) =(1+cos θ)[((4c^2 )/((1−sin θ)^2 ))−1] 2(1−sin θ)^3 =(1+cos θ){4c^2 −(1−sin θ)^2 } ......](Q158257.png)
