
Question Number 1559 by 123456 last updated on 19/Aug/15
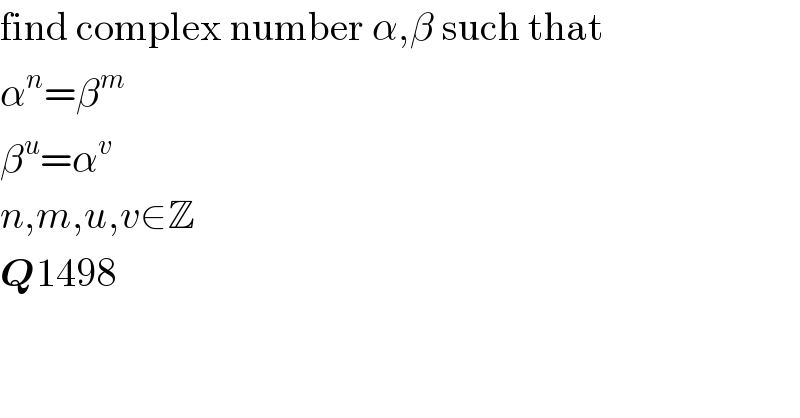
$$\mathrm{find}\:\mathrm{complex}\:\mathrm{number}\:\alpha,\beta\:\mathrm{such}\:\mathrm{that} \\ $$$$\alpha^{{n}} =\beta^{{m}} \\ $$$$\beta^{{u}} =\alpha^{{v}} \\ $$$${n},{m},{u},{v}\in\mathbb{Z} \\ $$$$\boldsymbol{{Q}}\mathrm{1498} \\ $$
Answered by Rasheed Soomro last updated on 19/Aug/15
![Let gcd(m,u)=k ⇒ lcm(m,u)=((mu)/k) (α^n )^(u/k) =(β^( m) )^(u/k) ⇒α^((nu)/k) =β^((mu)/k) ........(I) (β^( u) )^(m/k) =(α^v )^(m/k) ⇒β^( ((mu)/k)) =α^((mv)/k) .........(II) [In order to acheive the common exponent(least also) of β] From (I) and (II) α^((nu)/k) =α^((mv)/k) ⇒nu=mv [This condition is regardless of value of α and β] α^((nu)/k) − α^((mv)/k) =0 α^((mv)/k) (α^(((nu)/k)−((mv)/k)) −1)=0 ⇒ α^((mv)/k) =0 ∨ α^(((nu)/k)−((mv)/k)) −1=0 α=0 ∨ α^(((nu)/k)−((mv)/k)) =1 [You may equally proceed as α^((nu)/k) (1−α^(((mv)/k)−((nu)/k)) )=0 ⇒α^((nu)/k) =0 ∨ 1−α^(((mv)/k)−((nu)/k)) =0 ⇒ α=0 ∨ α^(((mv)/k)−((nu)/k)) =1⇒α^(((nu)/k)−((mv)/k)) =(1)^(−1) =1 same as above.] So α=^((nu−mv)/k) (√1) I−E α is ( ((nu−mv)/(gcd(m,u))) )th root of unity. Similar process shows that β=0 ∨ β is ( ((nu−mv)/(gcd(n,v))) )th root of unity. Solution for α {0}∪{1,ω,ω^2 ,......ω^((((nu−mv)/(gcd(m,u)))−1)) }; ω is ( ((nu−mv)/(gcd(m,u))) )th root of unity. Solution for β {0}∪{1,μ,μ^2 ,....μ^((((nu−mv)/(gcd(n,v)))−1)) }; μ is ( ((nu−mv)/(gcd(n,v))) )th root of unity. Let (α,β)=(ω^( p) ,μ^q ) such that α^n =β^( m) ∧ β^( u) =α^v (ω^( p) )^n =(μ^q )^m ∧ (μ^q )^u =(ω^( p) )^v ω^(np) =μ^(mq) ∧ μ^(uq) =ω^( vp) On simplication we get mv=nu , Which is free of p and q and that means p and q may be any integers. Hence if A_α ={1,ω,ω^2 ,......ω^((((nu−mv)/(gcd(m,u)))−1)) } and A_β ={1,μ,μ^2 ,....μ^((((nu−mv)/(gcd(n,v)))−1)) } , the solution for pair (α,β) is whole A_α ×A_β](Q1560.png)
$${Let}\:{gcd}\left({m},{u}\right)={k}\:\Rightarrow\:{lcm}\left({m},{u}\right)=\frac{{mu}}{{k}} \\ $$$$\left(\alpha^{{n}} \right)^{\frac{{u}}{{k}}} =\left(\beta^{\:{m}} \right)^{\frac{{u}}{{k}}} \:\Rightarrow\alpha^{\frac{{nu}}{{k}}} =\beta^{\frac{{mu}}{{k}}} \:\:\:\:\:\:\:\:\:\:\:\:........\left(\boldsymbol{{I}}\right)\: \\ $$$$\left(\beta^{\:{u}} \right)^{\frac{{m}}{{k}}} =\left(\alpha^{{v}} \right)^{\frac{{m}}{{k}}} \:\Rightarrow\beta^{\:\frac{{mu}}{{k}}} =\alpha^{\frac{{mv}}{{k}}} \:\:\:\:\:\:\:\:\:\:\:.........\left(\boldsymbol{{II}}\right) \\ $$$$\left[{In}\:{order}\:{to}\:{acheive}\:{the}\:{common}\:{exponent}\left({least}\:{also}\right)\:\:{of}\:\beta\right] \\ $$$${From}\:\left(\boldsymbol{{I}}\right)\:{and}\:\left(\boldsymbol{{II}}\right) \\ $$$$\:\:\:\:\alpha^{\frac{{nu}}{{k}}} =\alpha^{\frac{{mv}}{{k}}} \Rightarrow{nu}={mv}\:\:\:\left[{This}\:{condition}\:{is}\:{regardless}\:\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{of}\:{value}\:{of}\:\alpha\:{and}\:\beta\right] \\ $$$$\:\:\:\alpha^{\frac{{nu}}{{k}}} −\:\alpha^{\frac{{mv}}{{k}}} =\mathrm{0} \\ $$$$\:\:\:\alpha^{\frac{{mv}}{{k}}} \left(\alpha^{\frac{{nu}}{{k}}−\frac{{mv}}{{k}}} −\mathrm{1}\right)=\mathrm{0}\:\Rightarrow\:\:\:\alpha^{\frac{{mv}}{{k}}} =\mathrm{0}\:\vee\:\:\alpha^{\frac{{nu}}{{k}}−\frac{{mv}}{{k}}} −\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\alpha=\mathrm{0}\:\vee\:\alpha^{\frac{{nu}}{{k}}−\frac{{mv}}{{k}}} =\mathrm{1} \\ $$$$\left[{You}\:{may}\:{equally}\:{proceed}\:{as}\:\right. \\ $$$$\:\:\:\:\:\:\alpha^{\frac{{nu}}{{k}}} \left(\mathrm{1}−\alpha^{\frac{{mv}}{{k}}−\frac{{nu}}{{k}}} \right)=\mathrm{0}\:\Rightarrow\alpha^{\frac{{nu}}{{k}}} =\mathrm{0}\:\vee\:\mathrm{1}−\alpha^{\frac{{mv}}{{k}}−\frac{{nu}}{{k}}} =\mathrm{0} \\ $$$$\left.\Rightarrow\:\alpha=\mathrm{0}\:\vee\:\alpha^{\frac{{mv}}{{k}}−\frac{{nu}}{{k}}} =\mathrm{1}\Rightarrow\alpha^{\frac{{nu}}{{k}}−\frac{{mv}}{{k}}} =\left(\mathrm{1}\right)^{−\mathrm{1}} =\mathrm{1}\:{same}\:{as}\:{above}.\right] \\ $$$$\:\:{So}\:\alpha=^{\frac{{nu}−{mv}}{{k}}} \sqrt{\mathrm{1}} \\ $$$${I}−{E}\:\:\alpha\:{is}\:\left(\:\frac{{nu}−{mv}}{{gcd}\left({m},{u}\right)}\:\right)\boldsymbol{{th}}\:{root}\:{of}\:{unity}. \\ $$$${Similar}\:{process}\:{shows}\:{that} \\ $$$$\beta=\mathrm{0}\:\vee\:\beta\:\:{is}\:\:\:\left(\:\frac{{nu}−{mv}}{{gcd}\left({n},{v}\right)}\:\right)\boldsymbol{{th}}\:\:{root}\:{of}\:{unity}. \\ $$$${Solution}\:{for}\:\alpha \\ $$$$\:\:\:\:\left\{\mathrm{0}\right\}\cup\left\{\mathrm{1},\omega,\omega^{\mathrm{2}} ,......\omega^{\left(\frac{{nu}−{mv}}{{gcd}\left({m},{u}\right)}−\mathrm{1}\right)} \right\};\:\omega\:{is}\:\left(\:\frac{{nu}−{mv}}{{gcd}\left({m},{u}\right)}\:\right)\boldsymbol{{th}}\:{root}\:{of}\:{unity}. \\ $$$${Solution}\:{for}\:\beta \\ $$$$\:\:\:\:\left\{\mathrm{0}\right\}\cup\left\{\mathrm{1},\mu,\mu^{\mathrm{2}} ,....\mu^{\left(\frac{{nu}−{mv}}{{gcd}\left({n},{v}\right)}−\mathrm{1}\right)} \right\};\:\mu\:{is}\:\left(\:\frac{{nu}−{mv}}{{gcd}\left({n},{v}\right)}\:\right)\boldsymbol{{th}}\:\:{root}\:{of}\:{unity}. \\ $$$${Let}\:\left(\alpha,\beta\right)=\left(\omega^{\:{p}} \:,\mu^{{q}} \right)\:{such}\:{that} \\ $$$$\:\:\:\:\:\alpha^{{n}} =\beta^{\:{m}} \:\wedge\:\beta^{\:{u}} =\alpha^{{v}} \\ $$$$\:\:\:\:\:\left(\omega^{\:{p}} \right)^{{n}} =\left(\mu^{{q}} \right)^{{m}} \:\:\wedge\:\:\:\left(\mu^{{q}} \right)^{{u}} =\left(\omega^{\:{p}} \right)^{{v}} \\ $$$$\:\:\:\:\omega^{{np}} =\mu^{{mq}} \:\:\:\wedge\:\:\:\:\mu^{{uq}} =\omega^{\:{vp}} \\ $$$${On}\:{simplication}\:{we}\:{get} \\ $$$$\:\:\:\:\:{mv}={nu}\:\:\:,\:\:{Which}\:{is}\:{free}\:{of}\:\:{p}\:\:{and}\:\:\:{q}\:\:\:{and}\:\:{that}\:{means} \\ $$$${p}\:\:{and}\:\:{q}\:{may}\:{be}\:{any}\:{integers}. \\ $$$${Hence}\:{if} \\ $$$$\:\:\:\:\:\:\:\:\:\:{A}_{\alpha} =\left\{\mathrm{1},\omega,\omega^{\mathrm{2}} ,......\omega^{\left(\frac{{nu}−{mv}}{{gcd}\left({m},{u}\right)}−\mathrm{1}\right)} \right\}\:\: \\ $$$${and}\:\:\:{A}_{\beta} =\left\{\mathrm{1},\mu,\mu^{\mathrm{2}} ,....\mu^{\left(\frac{{nu}−{mv}}{{gcd}\left({n},{v}\right)}−\mathrm{1}\right)} \right\}\:\:,\:{the}\:{solution}\:{for}\:{pair} \\ $$$$\left(\alpha,\beta\right)\:\:{is}\:{whole}\:\:{A}_{\alpha} ×{A}_{\beta} \\ $$
Answered by Rasheed Soomro last updated on 19/Aug/15

$$\alpha\:{and}\:\beta\:{may}\:{be}\:{any}\:{complex}\:{numbers}\:{for} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{mv}={nu} \\ $$
