
Question and Answers Forum
Question Number 156008 by zainaltanjung last updated on 07/Oct/21

Commented by SANOGO last updated on 07/Oct/21

Commented by puissant last updated on 07/Oct/21
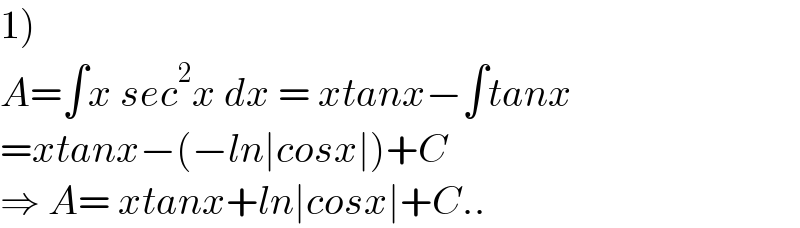
Commented by puissant last updated on 07/Oct/21
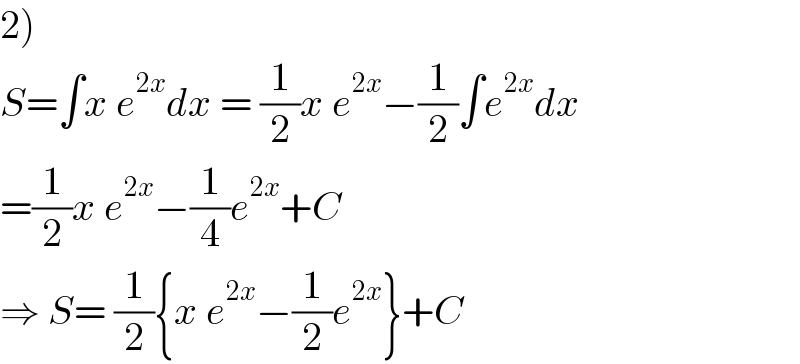
Commented by SANOGO last updated on 07/Oct/21

Commented by puissant last updated on 07/Oct/21

Commented by puissant last updated on 07/Oct/21
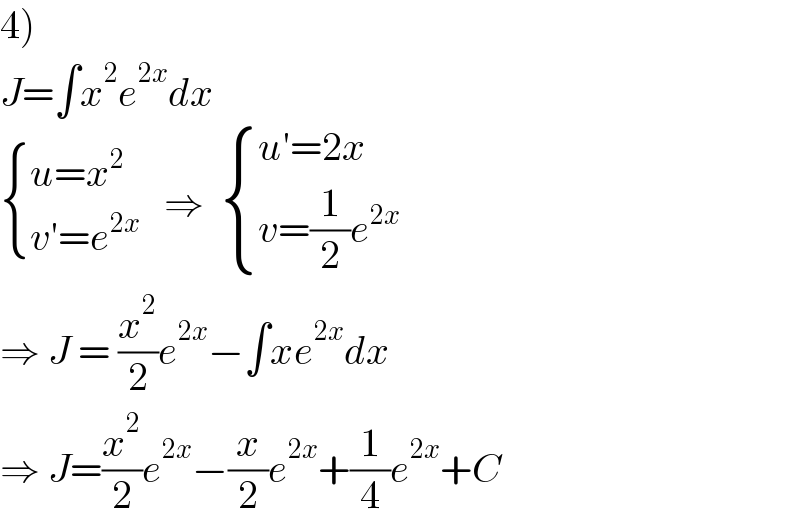
Commented by puissant last updated on 07/Oct/21
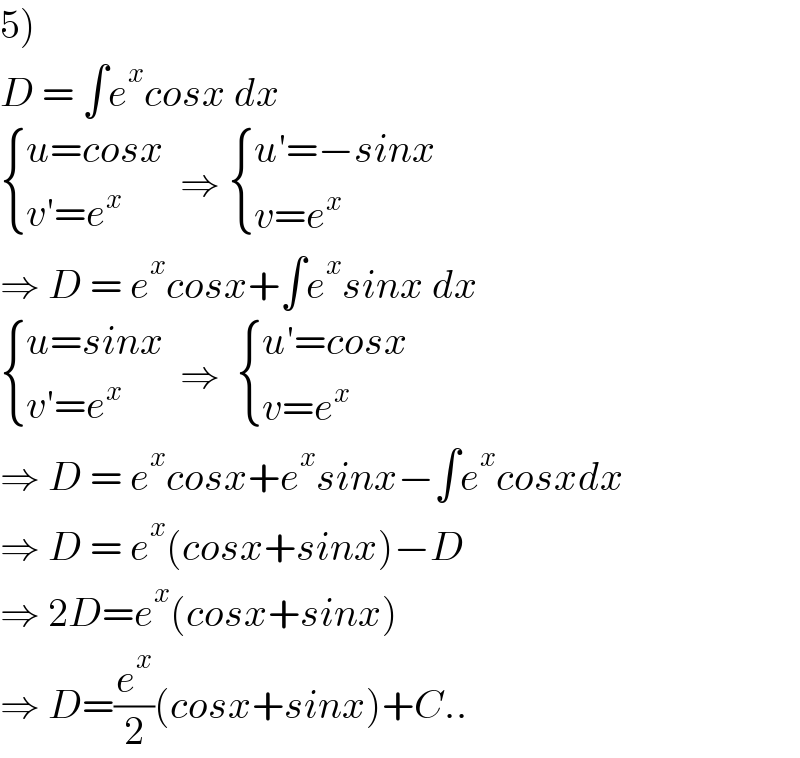
Commented by tabata last updated on 08/Oct/21

