
Question Number 156517 by cortano last updated on 12/Oct/21
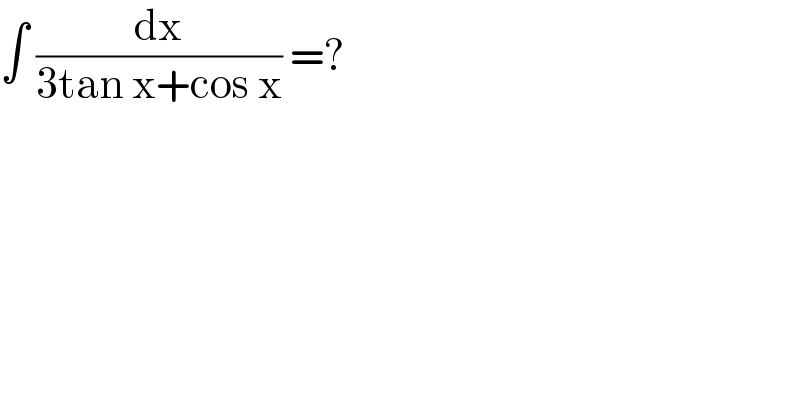
$$\int\:\frac{\mathrm{dx}}{\mathrm{3tan}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:=? \\ $$
Answered by puissant last updated on 12/Oct/21
![Q=∫(dx/(3tanx+cosx)) =∫((cosx)/(cos^2 x+3sinx))dx = ∫((cosx)/(1−sin^2 +3sinx))dx u=sinx → du=cosxdx ⇒ Q=∫(du/(1+3u−u^2 )) ⇒ Q=∫(du/(((13)/4)−((3/2)−u)^2 )) ⇒ Q=(4/(13))∫(du/(1−[(2/( (√(13))))((3/2)−u)]^2 )) t=(2/( (√(13))))((3/2)−u) → dt=−(2/( (√(13))))du→du=−((√(13))/2)dt ⇒ Q=(4/(13))×((√(13))/2)∫(dt/(t^2 −1))⇒ Q=(2/( (√(13))))argth(t)+C ⇒ Q=(2/( (√(13)))) argth(((3−2u)/( (√(13)))))+C ∴∵ Q=∫(dx/(3tanx+cosx))=(2/( (√(13))))argth(((3−2sinx)/( (√(13)))))+C ..............Le puissant............](Q156518.png)
$${Q}=\int\frac{{dx}}{\mathrm{3}{tanx}+{cosx}} \\ $$$$=\int\frac{{cosx}}{{cos}^{\mathrm{2}} {x}+\mathrm{3}{sinx}}{dx}\:=\:\int\frac{{cosx}}{\mathrm{1}−{sin}^{\mathrm{2}} +\mathrm{3}{sinx}}{dx} \\ $$$${u}={sinx}\:\rightarrow\:{du}={cosxdx} \\ $$$$\Rightarrow\:{Q}=\int\frac{{du}}{\mathrm{1}+\mathrm{3}{u}−{u}^{\mathrm{2}} }\:\Rightarrow\:{Q}=\int\frac{{du}}{\frac{\mathrm{13}}{\mathrm{4}}−\left(\frac{\mathrm{3}}{\mathrm{2}}−{u}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:{Q}=\frac{\mathrm{4}}{\mathrm{13}}\int\frac{{du}}{\mathrm{1}−\left[\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}\left(\frac{\mathrm{3}}{\mathrm{2}}−{u}\right)\right]^{\mathrm{2}} } \\ $$$${t}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}\left(\frac{\mathrm{3}}{\mathrm{2}}−{u}\right)\:\rightarrow\:{dt}=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}{du}\rightarrow{du}=−\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}{dt} \\ $$$$\Rightarrow\:{Q}=\frac{\mathrm{4}}{\mathrm{13}}×\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}\Rightarrow\:{Q}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}{argth}\left({t}\right)+{C} \\ $$$$\Rightarrow\:{Q}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}\:{argth}\left(\frac{\mathrm{3}−\mathrm{2}{u}}{\:\sqrt{\mathrm{13}}}\right)+{C} \\ $$$$ \\ $$$$\therefore\because\:{Q}=\int\frac{{dx}}{\mathrm{3}{tanx}+{cosx}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{13}}}{argth}\left(\frac{\mathrm{3}−\mathrm{2}{sinx}}{\:\sqrt{\mathrm{13}}}\right)+{C} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:..............\mathscr{L}{e}\:{puissant}............ \\ $$
Commented by cortano last updated on 12/Oct/21

$$\mathrm{okay}.\:\mathrm{my}\:\mathrm{answer}\:\mathrm{not}\:\mathrm{in}\:\mathrm{arctanh}\: \\ $$
Commented by ARUNG_Brandon_MBU last updated on 12/Oct/21
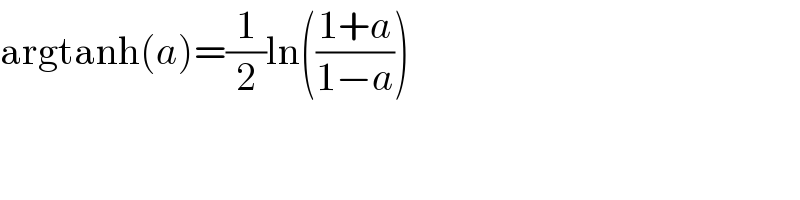
$$\mathrm{argtanh}\left({a}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}\right) \\ $$
