Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 156610 by jlewis last updated on 13/Oct/21

$$\mathrm{If}\mathrm{A}\mathrm{and}\mathrm{B}\mathrm{are}\mathrm{invertible}\mathrm{matrices},\mathrm{then}:$$$${\left(\mathrm{AB}\right)}^{-1}={\mathrm{B}}^{-1}{\mathrm{A}}^{-1}\ne {\mathrm{A}}^{-1}{\mathrm{B}}^{-1}$$$$\mathbf{proove}.$$

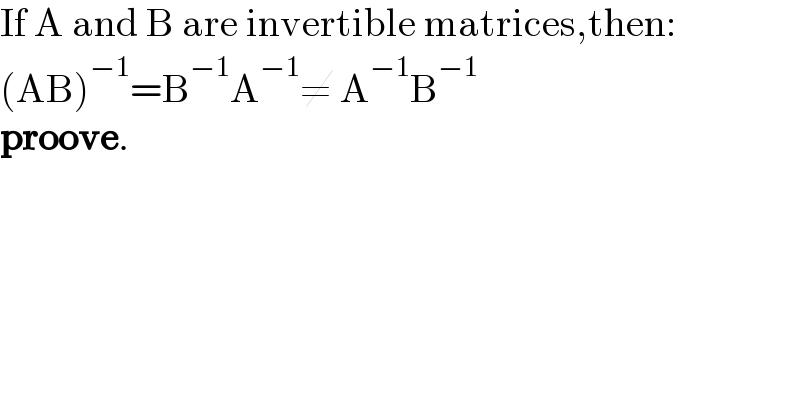
Answered by physicstutes last updated on 14/Oct/21

$$\mathrm{Consider}\mathrm{the}\mathrm{theorems}{AA}^{-1}=I$$$$\mathrm{and}{BB}^{-1}=I$$$$\mathrm{now}\mathrm{assume}:{\left(AB\right)}^{-1}=B^{-1}{A}^{-1}$$$$\mathrm{pre}-\mathrm{multiply}\mathrm{both}\mathrm{sides}\mathrm{by}AB$$$$\Rightarrow AB{\left(AB\right)}^{-1}={ABB}^{-1}{A}^{-1}$$$$\Rightarrow I={AIA}^{-1}$$$$\Rightarrow I={AA}^{-1}$$$$\Rightarrow I=I\mathrm{which}\mathrm{is}\mathrm{true}!$$$$\mathrm{Also}\mathrm{consider}:$$$${\left(AB\right)}^{-1}=A^{-1}{B}^{-1}$$$$\mathrm{pre}-\mathrm{multiply}\mathrm{both}\mathrm{sides}\mathrm{by}AB$$$$\Rightarrow \left(AB\right){\left(AB\right)}^{-1}={ABA}^{-1}{B}^{-1}$$$$\Rightarrow I\ne {ABA}^{-1}{B}^{-1}$$

Answered by TheSupreme last updated on 13/Oct/21

$$B^{-1}{A}^{-1}AB=B^{-1}\left(A^{-1}A\right)B=B^{-1}B=I$$$$theinequalitycanbedemonstratewithnoncommutativityofmatrixmoltiplication$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com