Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 156676 by mathlove last updated on 14/Oct/21

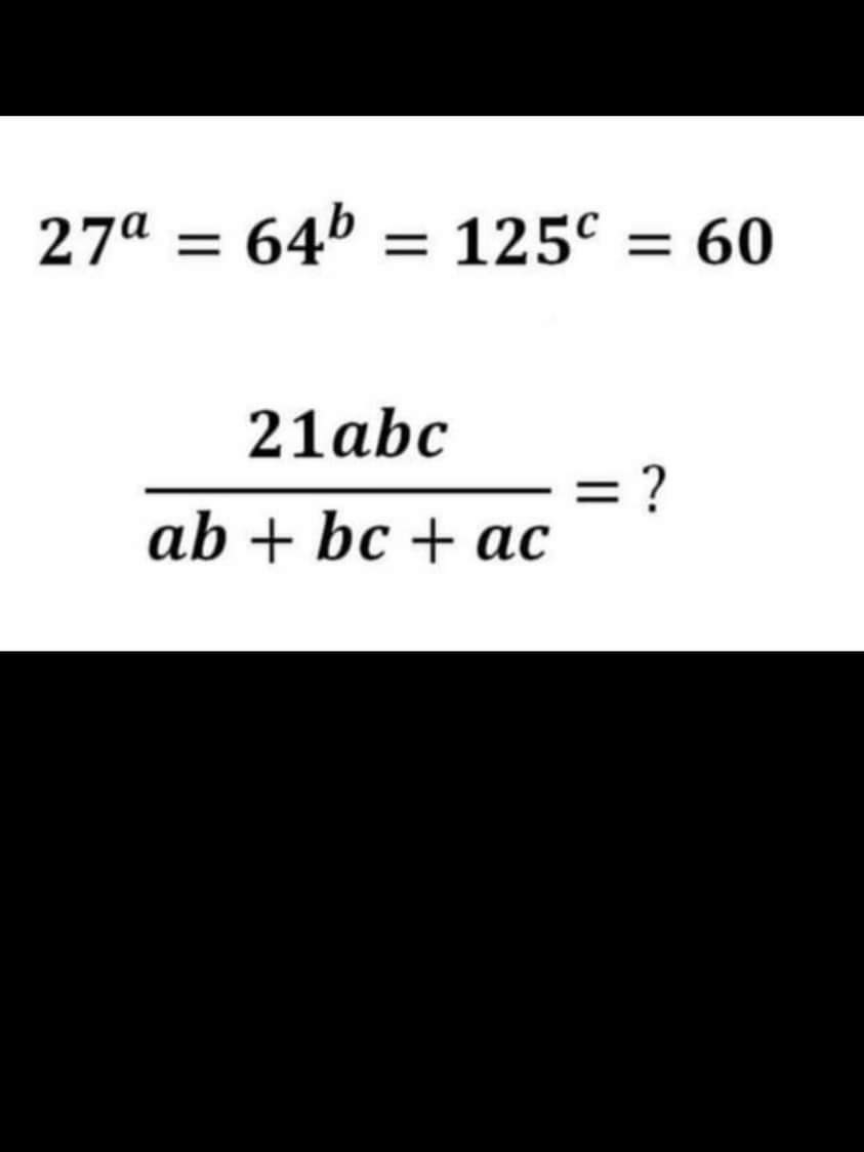
Commented by MathSh last updated on 14/Oct/21

$$\frac{2}{\mathrm{a}}+\frac{1}{\mathrm{b}}+\frac{1}{\mathrm{c}}=3\Rightarrow \frac{21}{3}=7$$

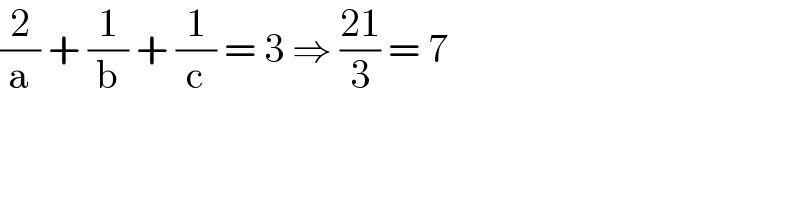
Answered by som(math1967) last updated on 14/Oct/21

$$60={27}^a\Rightarrow {60}^{\frac{1}{a}}=27$$$${60}^{\frac{1}{b}}=64,{60}^{\frac{1}{c}}=125$$$${60}^{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}}=3^3\times 4^3\times 5^3$$$${\left(60\right)}^{\frac{ab+bc+ca}{abc}}={\left(60\right)}^3$$$$\frac{ab+bc+ca}{abc}=3$$$$\frac{abc}{ab+bc+ca}=\frac{1}{3}$$$$\therefore \frac{21\mathit{a}\mathit{b}\mathit{c}}{\mathit{a}\mathit{b}+\mathit{b}\mathit{c}+\mathit{c}\mathit{a}}=21\times \frac{1}{3}=7\mathit{a}\mathit{n}\mathit{s}$$

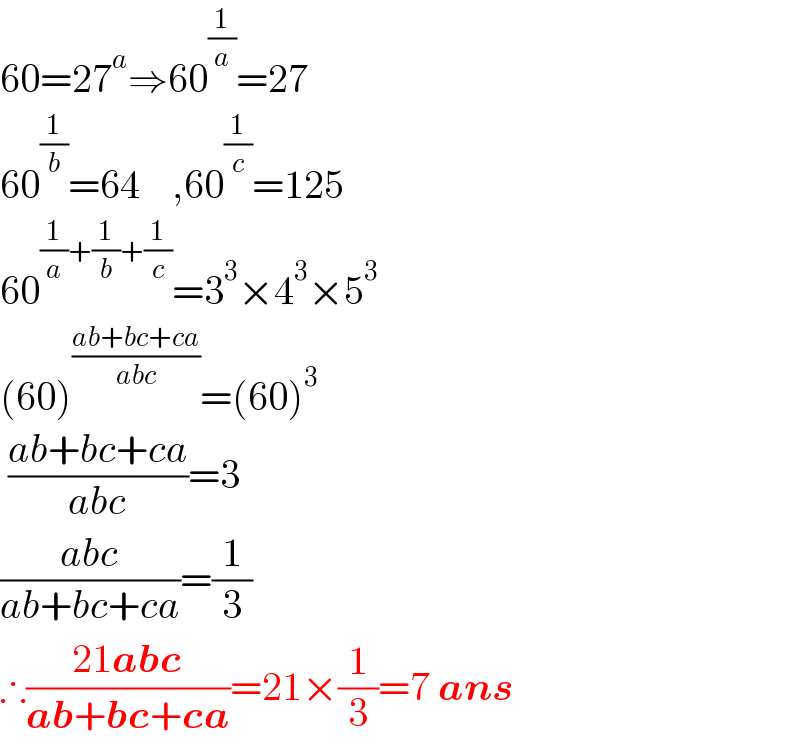
Answered by Rasheed.Sindhi last updated on 14/Oct/21

$$\mathbb{A}\mathrm{n}\mathbb{A}\mathrm{lternate}\mathbb{A}\mathrm{pproach}$$$${\left(3^a\right)}^3={\left(4^b\right)}^3={\left(5^c\right)}^3=60$$$${\left(3^a\right)}^3{\left(4^b\right)}^3{\left(5^c\right)}^3={\left(60\right)}^3$$$$3^a{4}^b{5}^c=60=3^1.4^1.5^1$$$$a=b=c=1$$$$\frac{21abc}{ab+bc+ca}=\frac{21.1.1.1}{1.1+1.1+1.1}=\frac{21}{3}=7$$$$$$

Commented by mr W last updated on 14/Oct/21

$$buta=b=c=1{doesn}^{\prime }tfulfillthe$$$$givencondition.$$

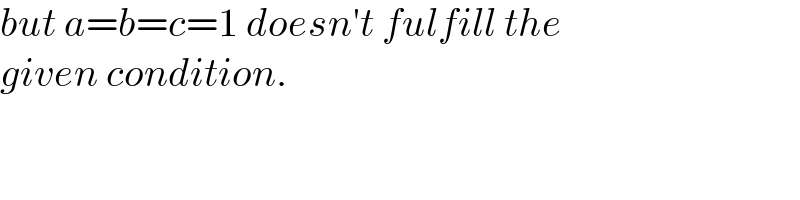
Commented by Rasheed.Sindhi last updated on 14/Oct/21

$$Yessirtheapproachis\mathit{l}\mathit{o}\mathit{g}\mathit{i}\mathit{c}\mathit{a}\mathit{l}\mathit{l}\mathit{y}$$$$\mathit{w}\mathit{r}\mathit{o}\mathit{n}\mathit{g}buttheansweris\mathit{b}\mathit{y}\mathit{c}\mathit{h}\mathit{a}\mathit{n}\mathit{c}\mathit{e}$$$$\mathit{r}\mathit{i}\mathit{g}\mathit{h}\mathit{t}!\mathcal{T}hankssir!$$

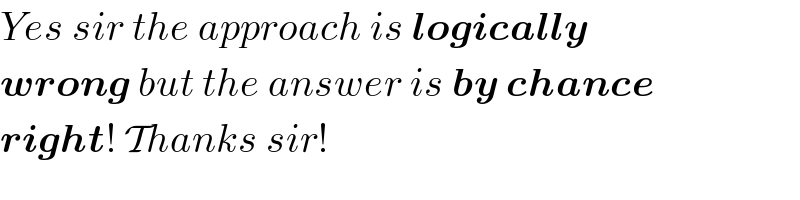
Answered by john_santu last updated on 14/Oct/21

$$\frac{21}{\frac{1}{c}+\frac{1}{a}+\frac{1}{b}}=k$$$$\{\begin{array}{l}{27}^a=60\Rightarrow a=\log {}_{27}\left(60\right)\\ {64}^b=60\Rightarrow b=\log {}_{64}\left(60\right)\\ {125}^c=60\Rightarrow c=\log {}_{125}\left(60\right)\end{array}$$$$thereforek=\frac{21}{\log {}_{60}\left(125\right)+\log {}_{60}\left(27\right)+\log {}_{60}\left(64\right)}$$$$k=\frac{21}{\log {}_{60}\left(125\times 27\times 64\right)}=\frac{27}{\log {}_{60}\left({60}^3\right)}$$$$k=\frac{21}{3\log {}_{60}\left(60\right)}=\frac{21}{3}=7.$$

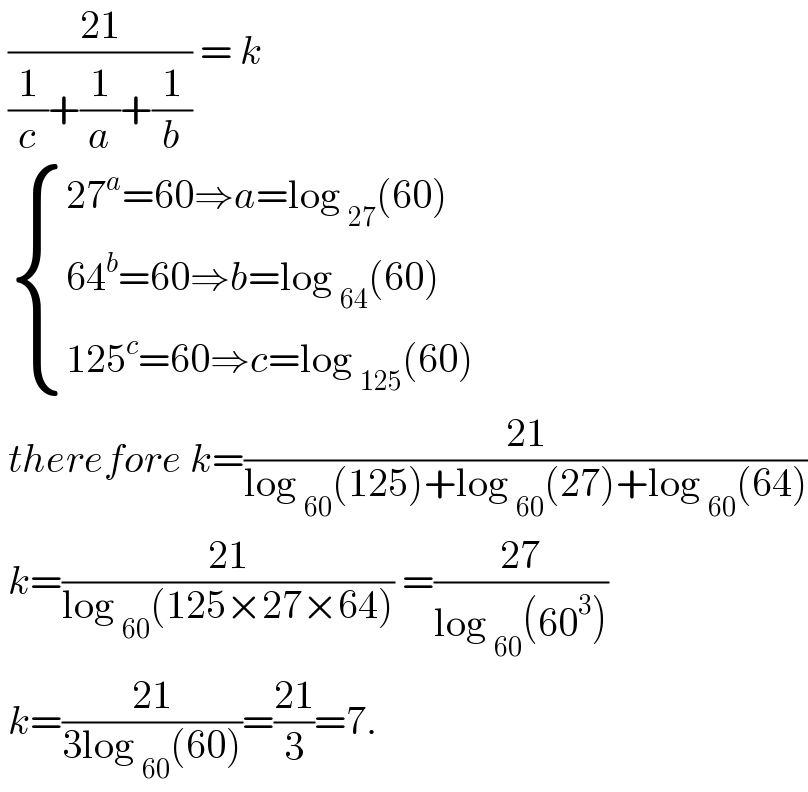
Commented by cortano last updated on 14/Oct/21

$$\mathrm{waw}$$$$$$

Commented by peter frank last updated on 14/Oct/21

$$\mathrm{great}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com