Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 156788 by mathlove last updated on 15/Oct/21

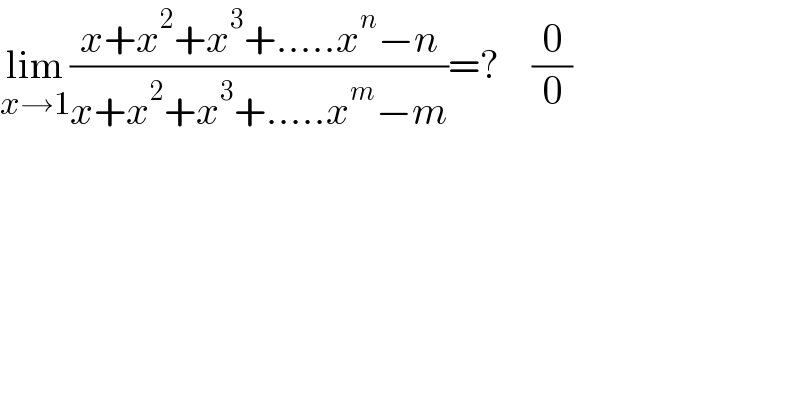
lim_(x→1) ((x+x^2 +x^3 +.....x^n −n)/(x+x^2 +x^3 +.....x^m −m))=? (0/0)

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +.....{x}^{{n}} −{n}}{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +.....{x}^{{m}} −{m}}=?\:\:\:\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$

Answered by puissant last updated on 15/Oct/21

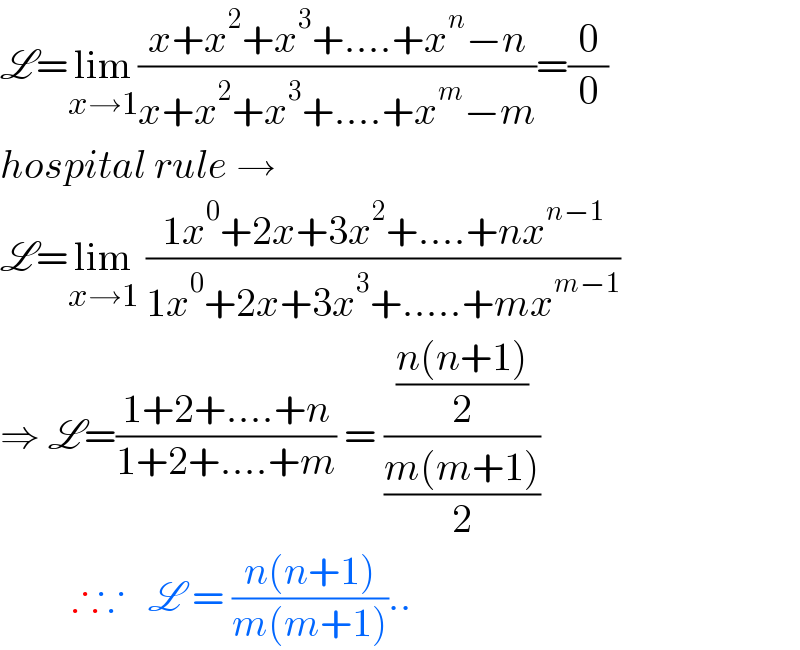
L=lim_(x→1) ((x+x^2 +x^3 +....+x^n −n)/(x+x^2 +x^3 +....+x^m −m))=(0/0) hospital rule → L=lim_(x→1) ((1x^0 +2x+3x^2 +....+nx^(n−1) )/(1x^0 +2x+3x^3 +.....+mx^(m−1) )) ⇒ L=((1+2+....+n)/(1+2+....+m)) = (((n(n+1))/2)/((m(m+1))/2)) ∴∵ L = ((n(n+1))/(m(m+1)))..

$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +....+{x}^{{n}} −{n}}{{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +....+{x}^{{m}} −{m}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$${hospital}\:{rule}\:\rightarrow\: \\ $$$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}{x}^{\mathrm{0}} +\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +....+{nx}^{{n}−\mathrm{1}} }{\mathrm{1}{x}^{\mathrm{0}} +\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{3}} +.....+{mx}^{{m}−\mathrm{1}} } \\ $$$$\Rightarrow\:\mathscr{L}=\frac{\mathrm{1}+\mathrm{2}+....+{n}}{\mathrm{1}+\mathrm{2}+....+{m}}\:=\:\frac{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}}{\frac{{m}\left({m}+\mathrm{1}\right)}{\mathrm{2}}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\therefore\because\:\:\:\mathscr{L}\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{{m}\left({m}+\mathrm{1}\right)}.. \\ $$

Commented by mathlove last updated on 15/Oct/21

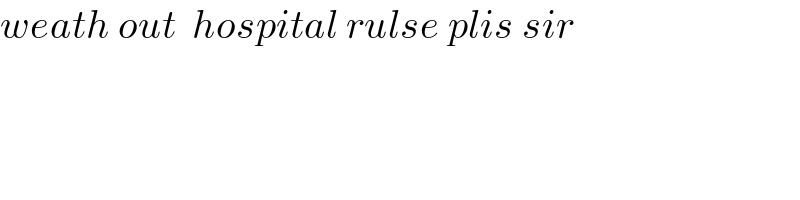
weath out hospital rulse plis sir

$${weath}\:{out}\:\:{hospital}\:{rulse}\:{plis}\:{sir} \\ $$

Commented by puissant last updated on 15/Oct/21

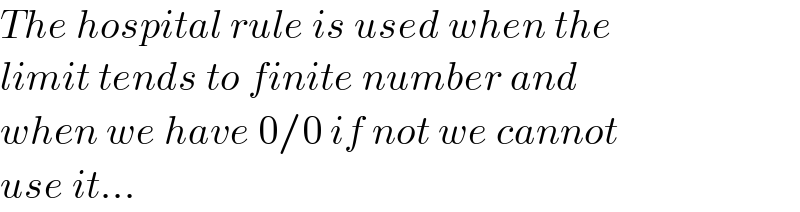
The hospital rule is used when the limit tends to finite number and when we have 0/0 if not we cannot use it...

$${The}\:{hospital}\:{rule}\:{is}\:{used}\:{when}\:{the}\: \\ $$$${limit}\:{tends}\:{to}\:{finite}\:{number}\:{and}\: \\ $$$${when}\:{we}\:{have}\:\mathrm{0}/\mathrm{0}\:{if}\:{not}\:{we}\:{cannot} \\ $$$${use}\:{it}... \\ $$

Answered by FongXD last updated on 15/Oct/21

Without L′hospital′s rule =lim_(x→1) (((x−1)+(x^2 −1)+(x^3 −1)+...+(x^n −1))/((x−1)+(x^2 −1)+(x^3 −1)+...+(x^m −1))) =lim_(x→1) (((x−1)[1+(x+1)+(x^2 +x+1)+...+(x^(n−1) +x^(n−2) +...+x+1)])/((x−1)[1+(x+1)+(x^2 +x+1)+...+(x^(m−1) +x^(m−2) +...+x+1)])) =lim_(x→1) ((1+(x+1)+(x^2 +x+1)+...+(x^(n−1) +x^(n−2) +...+x+1))/(1+(x+1)+(x^2 +x+1)+...+(x^(m−1) +x^(m−2) +...+x+1))) =((1+2+3+...+n)/(1+2+3+...+m))=(((n(n+1))/2)/((m(m+1))/2))=((n(n+1))/(m(m+1)))

$$\mathrm{Without}\:\mathrm{L}'\mathrm{hospital}'\mathrm{s}\:\mathrm{rule} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)+...+\left(\mathrm{x}^{\mathrm{n}} −\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)+...+\left(\mathrm{x}^{\mathrm{m}} −\mathrm{1}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left(\mathrm{x}−\mathrm{1}\right)\left[\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+...+\left(\mathrm{x}^{\mathrm{n}−\mathrm{1}} +\mathrm{x}^{\mathrm{n}−\mathrm{2}} +...+\mathrm{x}+\mathrm{1}\right)\right]}{\left(\mathrm{x}−\mathrm{1}\right)\left[\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+...+\left(\mathrm{x}^{\mathrm{m}−\mathrm{1}} +\mathrm{x}^{\mathrm{m}−\mathrm{2}} +...+\mathrm{x}+\mathrm{1}\right)\right]} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+...+\left(\mathrm{x}^{\mathrm{n}−\mathrm{1}} +\mathrm{x}^{\mathrm{n}−\mathrm{2}} +...+\mathrm{x}+\mathrm{1}\right)}{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+...+\left(\mathrm{x}^{\mathrm{m}−\mathrm{1}} +\mathrm{x}^{\mathrm{m}−\mathrm{2}} +...+\mathrm{x}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{n}}{\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\mathrm{m}}=\frac{\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}}{\frac{\mathrm{m}\left(\mathrm{m}+\mathrm{1}\right)}{\mathrm{2}}}=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{m}\left(\mathrm{m}+\mathrm{1}\right)} \\ $$

Commented by mathlove last updated on 16/Oct/21

thanks sir

$${thanks}\:{sir} \\ $$

Commented by Rasheed.Sindhi last updated on 16/Oct/21

Nice Sir!

$$\mathcal{N}{ice}\:\mathcal{S}{ir}! \\ $$

Answered by mindispower last updated on 16/Oct/21

x+x^2 +x^3 +.....+x^n −n= (x−1)(x^(n−1) +2x^(n−2) +..kx^(k−1) +....+n) x+x^2 +.....+x^m −m=(x−1)(x^(m−1) +.2x^(m−2) +.....+m) ⇔lim_(x→0) .((n+(n−1)x+...(k−1)x^(k−1) +...+x)/(m+(m−1)+....+(k−1)x^(k−1) +..+x)) =((Σ_(k=1) ^n k)/(Σ_(k=1) ^m k))=((n(n+1))/(m(m+1)))

$${x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +.....+{x}^{{n}} −{n}= \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{{n}−\mathrm{1}} +\mathrm{2}{x}^{{n}−\mathrm{2}} +..{kx}^{{k}−\mathrm{1}} +....+{n}\right) \\ $$$${x}+{x}^{\mathrm{2}} +.....+{x}^{{m}} −{m}=\left({x}−\mathrm{1}\right)\left({x}^{{m}−\mathrm{1}} +.\mathrm{2}{x}^{{m}−\mathrm{2}} +.....+{m}\right) \\ $$$$\Leftrightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}.\frac{\boldsymbol{{n}}+\left(\boldsymbol{{n}}−\mathrm{1}\right){x}+...\left({k}−\mathrm{1}\right){x}^{{k}−\mathrm{1}} +...+\boldsymbol{{x}}}{\boldsymbol{{m}}+\left(\boldsymbol{{m}}−\mathrm{1}\right)+....+\left(\boldsymbol{{k}}−\mathrm{1}\right)\boldsymbol{{x}}^{\boldsymbol{{k}}−\mathrm{1}} +..+\boldsymbol{{x}}} \\ $$$$=\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}}{\underset{{k}=\mathrm{1}} {\overset{{m}} {\sum}}{k}}=\frac{{n}\left({n}+\mathrm{1}\right)}{{m}\left({m}+\mathrm{1}\right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com