
Question and Answers Forum
Question Number 156914 by cortano last updated on 17/Oct/21
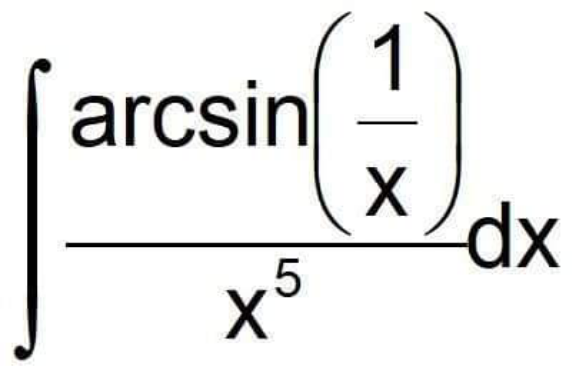
Answered by puissant last updated on 17/Oct/21
![D=∫((arcsin((1/x)))/x^5 )dx ; u=(1/x) → du=−(1/x^2 )dx ⇒ D=−∫ ((u^5 arcsin(u))/u^2 )du=−∫u^3 arcsin(u)du IBP⇒ D=−3[u^2 arcsin(u)]+3∫(u^2 /( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−3∫((1−u^2 −1)/( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−3∫(√(1−u^2 ))+3∫(1/( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−(3/2)[t+(1/2)sin2t]+3arcsin(u)+C ⇒ D=((−3)/x^2 )arcsin((1/x))−(3/2)arcsin((1/x))−(3/2)sin(2arcsin((1/x)))+3arcsin((1/x))+C ∴∵ D=3{((1/2)−(1/x^2 ))arcsin((1/x))−(1/2)sin(2arcsin((1/x)))}+C..](Q156917.png)
Commented by cortano last updated on 17/Oct/21

Answered by cortano last updated on 17/Oct/21

| ||
Question and Answers Forum | ||
Question Number 156914 by cortano last updated on 17/Oct/21 | ||
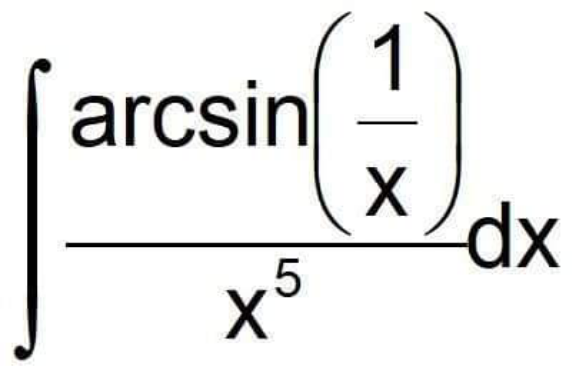 | ||
Answered by puissant last updated on 17/Oct/21 | ||
![D=∫((arcsin((1/x)))/x^5 )dx ; u=(1/x) → du=−(1/x^2 )dx ⇒ D=−∫ ((u^5 arcsin(u))/u^2 )du=−∫u^3 arcsin(u)du IBP⇒ D=−3[u^2 arcsin(u)]+3∫(u^2 /( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−3∫((1−u^2 −1)/( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−3∫(√(1−u^2 ))+3∫(1/( (√(1−u^2 ))))du ⇒ D=−3u^2 arcsin(u)−(3/2)[t+(1/2)sin2t]+3arcsin(u)+C ⇒ D=((−3)/x^2 )arcsin((1/x))−(3/2)arcsin((1/x))−(3/2)sin(2arcsin((1/x)))+3arcsin((1/x))+C ∴∵ D=3{((1/2)−(1/x^2 ))arcsin((1/x))−(1/2)sin(2arcsin((1/x)))}+C..](Q156917.png) | ||
| ||
Commented by cortano last updated on 17/Oct/21 | ||
 | ||
Answered by cortano last updated on 17/Oct/21 | ||
 | ||