
Question and Answers Forum
Question Number 156923 by MathSh last updated on 17/Oct/21
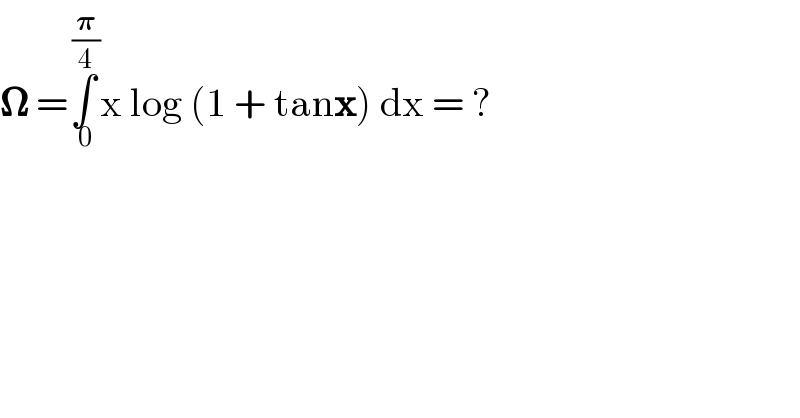
Answered by mindispower last updated on 18/Oct/21
![∫_0 ^(π/4) xln(cos(x))dx=a...? ln(cos(x))=−Σ_(k≥1) (((−1)^k cos(2kx))/k)−ln(2)..fourie sere a=−Σ_(k≥1) (((−1)^k )/k)∫_0 ^(π/4) xcos(2kx)dx−ln(2)∫_0 ^(π/4) xdx =−Σ_(k≥1) (((−1)^k )/k){[((xsin(2kx))/(2k))]_0 ^(π/4) +(1/(4k^2 ))[cos(2kx)]_0 ^(π/4) −(π^2 /(32))ln(2) =−(Σ_(k≥1) (((−1)^k sin(((kπ)/2)))/(2k^2 ))+(((−1)^k cos(((kπ)/2)))/(4k^3 ))) spit k=2m,k=2m+1we get withe sin(πm)=0 sin(πm+(π/2))=(−1)^m ,cos(mπ)=(−1)^m ,cos(mπ+(π/2))=(−1)^m =Σ_(m≥0) (((−1)^m )/(2(2m+1)^2 ))−Σ_(m≥1) (((−1)^m )/(32m^3 )) =(1/2)𝛃(−1)−(1/(32))Li_3 (−1)=(G/2)+(3/(4.32))ζ(3)−((π^2 ln(2))/(32)) ∫_0 ^(π/4) ln(cos(x))dx,∫_0 ^(π/4) ln(tg(x))=G ∫_0 ^(π/2) ln(sinx)dx=−(π/2)ln(2) cos(x)=(1/2)ln(((sin(x)cos(x))/(sin(x)))cos(x)),x∈[0,(π/2)] =(1/2)ln(sin(2x))−((ln(tg(x)))/2) ⇒∫_0 ^(π/4) ln(cos(x))=(π/8)ln(2)−(G/2) Ω=∫_0 ^(π/4) xln((((√2)sin(x+(π/4)))/(cos(x))))dx =((ln(2))/2)∫_0 ^(π/4) xdx+∫_0 ^(π/4) xln(sin(x+(π/4)))dx−∫_0 ^(π/4) xln(cos(x))dx =((ln(2))/(32))π^2 +∫_0 ^(π/4) (π/4)ln(cos(x))dx−2∫_0 ^(π/4) xln(cos(x))dx =((ln(2))/(32))π^2 +(π/4)(((πln2)/8)−(G/2))−2((G/2)+((3ζ(1))/(128))−((π^2 ln(2))/(32))) =−((π/8)+1)G+((π^2 ln(2))/8)−(3/(64))ζ(3)](Q157032.png)
Commented by MathSh last updated on 18/Oct/21
Commented by mindispower last updated on 19/Oct/21

| ||
Question and Answers Forum | ||
Question Number 156923 by MathSh last updated on 17/Oct/21 | ||
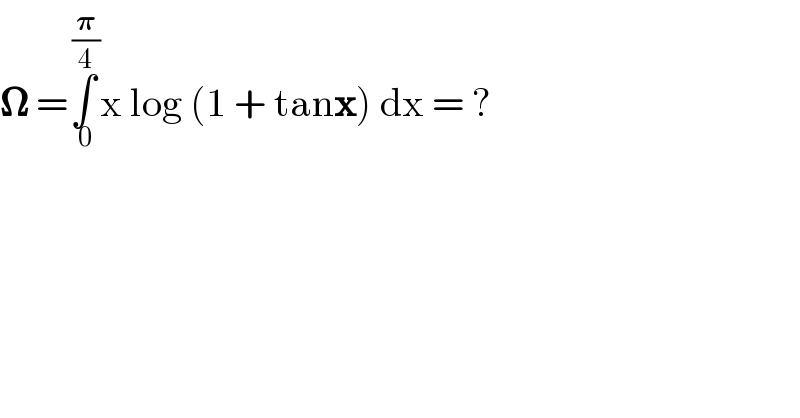 | ||
Answered by mindispower last updated on 18/Oct/21 | ||
![∫_0 ^(π/4) xln(cos(x))dx=a...? ln(cos(x))=−Σ_(k≥1) (((−1)^k cos(2kx))/k)−ln(2)..fourie sere a=−Σ_(k≥1) (((−1)^k )/k)∫_0 ^(π/4) xcos(2kx)dx−ln(2)∫_0 ^(π/4) xdx =−Σ_(k≥1) (((−1)^k )/k){[((xsin(2kx))/(2k))]_0 ^(π/4) +(1/(4k^2 ))[cos(2kx)]_0 ^(π/4) −(π^2 /(32))ln(2) =−(Σ_(k≥1) (((−1)^k sin(((kπ)/2)))/(2k^2 ))+(((−1)^k cos(((kπ)/2)))/(4k^3 ))) spit k=2m,k=2m+1we get withe sin(πm)=0 sin(πm+(π/2))=(−1)^m ,cos(mπ)=(−1)^m ,cos(mπ+(π/2))=(−1)^m =Σ_(m≥0) (((−1)^m )/(2(2m+1)^2 ))−Σ_(m≥1) (((−1)^m )/(32m^3 )) =(1/2)𝛃(−1)−(1/(32))Li_3 (−1)=(G/2)+(3/(4.32))ζ(3)−((π^2 ln(2))/(32)) ∫_0 ^(π/4) ln(cos(x))dx,∫_0 ^(π/4) ln(tg(x))=G ∫_0 ^(π/2) ln(sinx)dx=−(π/2)ln(2) cos(x)=(1/2)ln(((sin(x)cos(x))/(sin(x)))cos(x)),x∈[0,(π/2)] =(1/2)ln(sin(2x))−((ln(tg(x)))/2) ⇒∫_0 ^(π/4) ln(cos(x))=(π/8)ln(2)−(G/2) Ω=∫_0 ^(π/4) xln((((√2)sin(x+(π/4)))/(cos(x))))dx =((ln(2))/2)∫_0 ^(π/4) xdx+∫_0 ^(π/4) xln(sin(x+(π/4)))dx−∫_0 ^(π/4) xln(cos(x))dx =((ln(2))/(32))π^2 +∫_0 ^(π/4) (π/4)ln(cos(x))dx−2∫_0 ^(π/4) xln(cos(x))dx =((ln(2))/(32))π^2 +(π/4)(((πln2)/8)−(G/2))−2((G/2)+((3ζ(1))/(128))−((π^2 ln(2))/(32))) =−((π/8)+1)G+((π^2 ln(2))/8)−(3/(64))ζ(3)](Q157032.png) | ||
| ||
Commented by MathSh last updated on 18/Oct/21 | ||
 | ||
Commented by mindispower last updated on 19/Oct/21 | ||
 | ||