
Question and Answers Forum
Question Number 156993 by amin96 last updated on 18/Oct/21
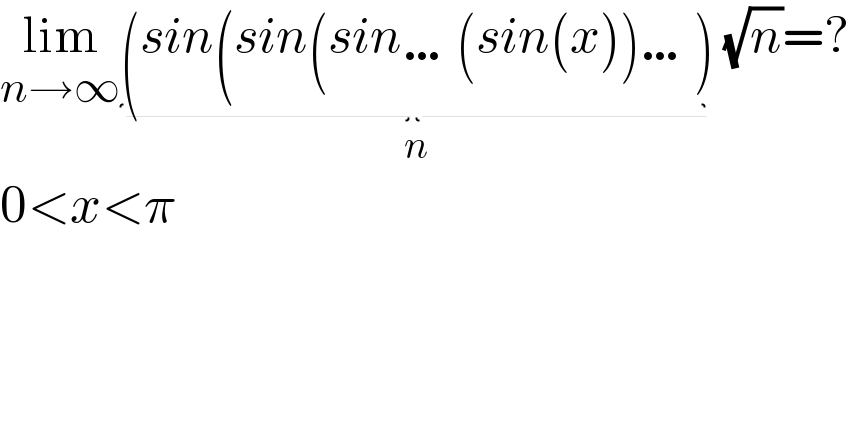
Commented byMathSh last updated on 18/Oct/21
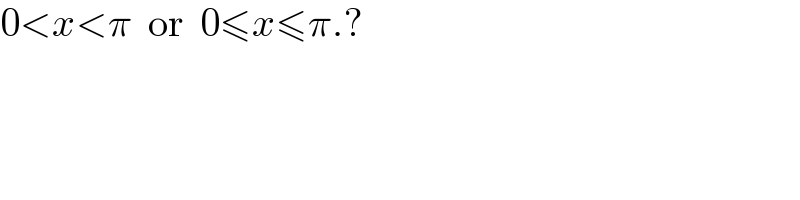
Commented byamin96 last updated on 18/Oct/21

Commented byMathSh last updated on 18/Oct/21
![a_x =lim_(n→∞) f_n (x) → a_x =sina_x → a_x =0 f_n (x)∼αn^(-r) f_(n+1) =sin f_n =f_n -((1/6))f_n ^3 +O(f_n ^5 ) αn^(-r) (1+(1/n))^(-r) ∼ αn^(-r) [1-((1/6))(αn^(-r) )^2 +O(n^(-4r) )] -rn^(-1) = - (α^2 /6) n^(-2r) α = (√3) → r = (1/2) ⇒lim_(n→∞) n^r f_n (x) = α = (√3) •](Q157005.png)
| ||
Question and Answers Forum | ||
Question Number 156993 by amin96 last updated on 18/Oct/21 | ||
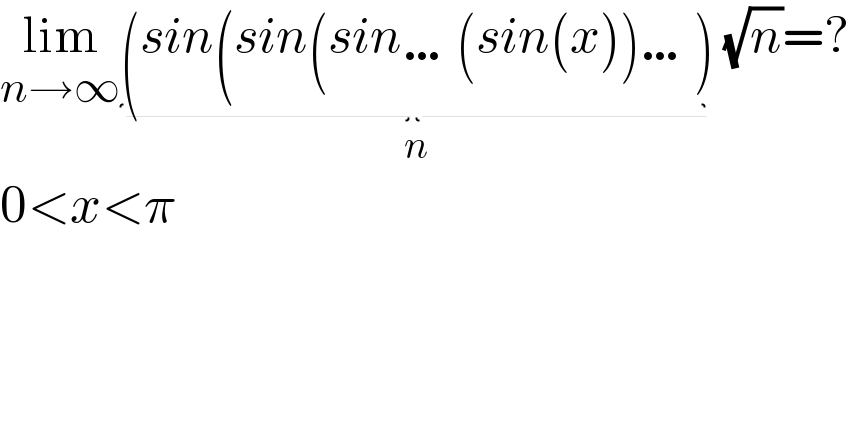 | ||
Commented byMathSh last updated on 18/Oct/21 | ||
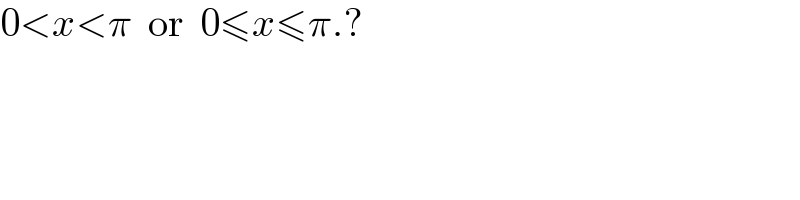 | ||
Commented byamin96 last updated on 18/Oct/21 | ||
 | ||
Commented byMathSh last updated on 18/Oct/21 | ||
![a_x =lim_(n→∞) f_n (x) → a_x =sina_x → a_x =0 f_n (x)∼αn^(-r) f_(n+1) =sin f_n =f_n -((1/6))f_n ^3 +O(f_n ^5 ) αn^(-r) (1+(1/n))^(-r) ∼ αn^(-r) [1-((1/6))(αn^(-r) )^2 +O(n^(-4r) )] -rn^(-1) = - (α^2 /6) n^(-2r) α = (√3) → r = (1/2) ⇒lim_(n→∞) n^r f_n (x) = α = (√3) •](Q157005.png) | ||