
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 157141 by cortano last updated on 20/Oct/21
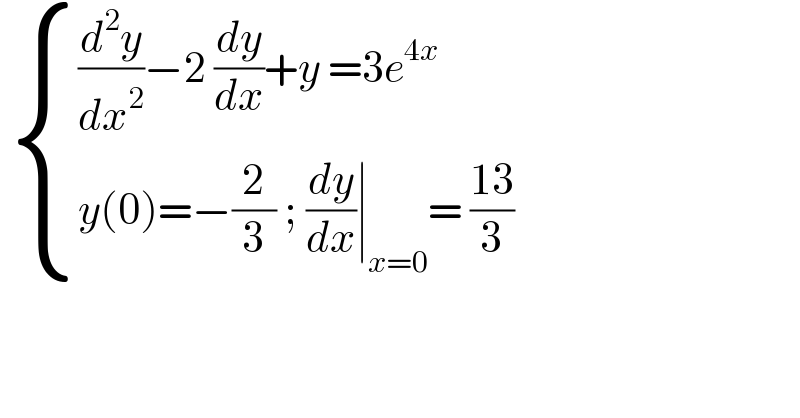
Commented by john_santu last updated on 21/Oct/21
![{ ((y′′−2y′+y=3e^(4x) )),((y(0)=−(2/3) ; y′(0)=((13)/3))) :} By wronskian method ⇒λ^2 −2λ+1=0⇒λ_(1,2) =1 ⇒y_h = Ae^x +Bxe^x Particular solution W(u_1 ,u_2 )= determinant (((e^x xe^x )),((e^x e^x +xe^x )))=e^(2x) W_1 = determinant (((0 xe^x )),((3e^(4x) e^x +xe^x )))=−3xe^(5x) W_2 = determinant (((e^x 0)),((e^x 3e^(4x) )))=3e^(5x) ⇒v_1 =∫ (w_1 /w) dx=∫ ((−3xe^(5x) )/e^(2x) ) dx =−3∫xe^(3x) dx =−3[ (1/3)xe^(3x) −(1/9)e^(3x) ]=−xe^(3x) +(1/3)e^(3x) ⇒v_2 =∫ (w_2 /w) dx=∫ ((3e^(5x) )/e^(2x) ) dx=∫3e^(3x) dx=e^(3x) ⇒y_p =u_1 v_1 +u_2 v_2 =e^x (−xe^(3x) +(1/3)e^(3x) )+xe^x (e^(3x) ) ⇒y_p =(1/3)e^(4x) y_g =Ae^x +Bxe^x +(1/3)e^(4x) { ((x=0⇒A+(1/3)=−(2/3) ; A=−1)),((y′=Ae^x +Be^x +Bxe^x +(4/3)e^(4x) )),((y′(0)=−1+B+(4/3)=((13)/3)⇒B=4 )) :} ⇔ ∴ y=−e^x +4xe^x +(1/3)e^(4x)](Q157239.png)
Answered by qaz last updated on 21/Oct/21
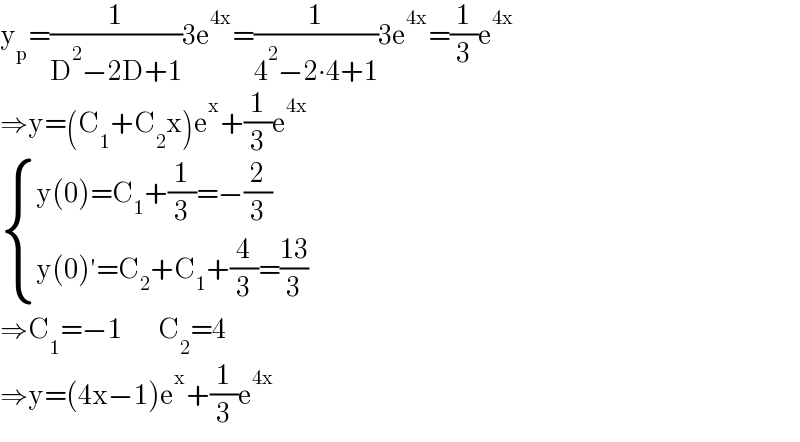
| ||
Question and Answers Forum | ||
Previous in Differential Equation Next in Differential Equation | ||
Question Number 157141 by cortano last updated on 20/Oct/21 | ||
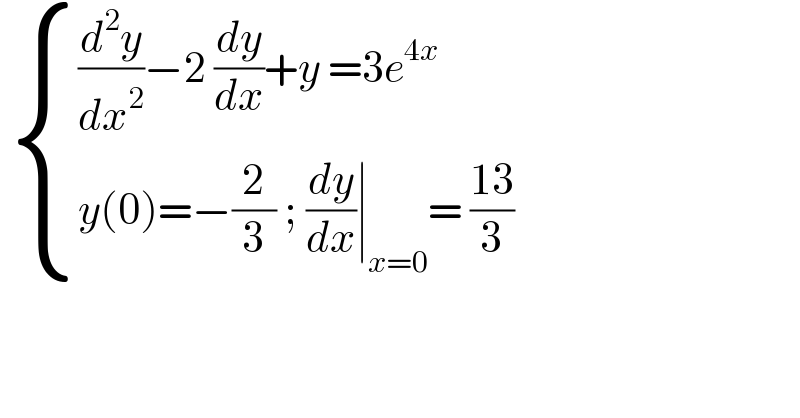 | ||
Commented by john_santu last updated on 21/Oct/21 | ||
![{ ((y′′−2y′+y=3e^(4x) )),((y(0)=−(2/3) ; y′(0)=((13)/3))) :} By wronskian method ⇒λ^2 −2λ+1=0⇒λ_(1,2) =1 ⇒y_h = Ae^x +Bxe^x Particular solution W(u_1 ,u_2 )= determinant (((e^x xe^x )),((e^x e^x +xe^x )))=e^(2x) W_1 = determinant (((0 xe^x )),((3e^(4x) e^x +xe^x )))=−3xe^(5x) W_2 = determinant (((e^x 0)),((e^x 3e^(4x) )))=3e^(5x) ⇒v_1 =∫ (w_1 /w) dx=∫ ((−3xe^(5x) )/e^(2x) ) dx =−3∫xe^(3x) dx =−3[ (1/3)xe^(3x) −(1/9)e^(3x) ]=−xe^(3x) +(1/3)e^(3x) ⇒v_2 =∫ (w_2 /w) dx=∫ ((3e^(5x) )/e^(2x) ) dx=∫3e^(3x) dx=e^(3x) ⇒y_p =u_1 v_1 +u_2 v_2 =e^x (−xe^(3x) +(1/3)e^(3x) )+xe^x (e^(3x) ) ⇒y_p =(1/3)e^(4x) y_g =Ae^x +Bxe^x +(1/3)e^(4x) { ((x=0⇒A+(1/3)=−(2/3) ; A=−1)),((y′=Ae^x +Be^x +Bxe^x +(4/3)e^(4x) )),((y′(0)=−1+B+(4/3)=((13)/3)⇒B=4 )) :} ⇔ ∴ y=−e^x +4xe^x +(1/3)e^(4x)](Q157239.png) | ||
Answered by qaz last updated on 21/Oct/21 | ||
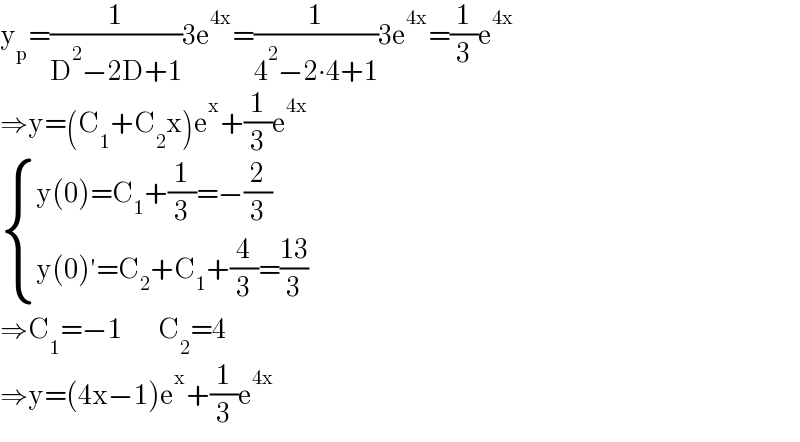 | ||
| ||