
Question and Answers Forum
Question Number 157175 by cortano last updated on 20/Oct/21

Commented by puissant last updated on 20/Oct/21

Answered by Mathspace last updated on 20/Oct/21
![I=∫_0 ^∞ ln(((1+e^(−x) )/(1−e^(−x) )))dx =∫_0 ^∞ ln(1+e^(−x) )dx−∫_0 ^∞ ln(1−e^(−x)) dx ln^′ (1+u)dx=(1/(1+u))=Σ(−1)^n u^n ⇒ ln(1+u)=Σ_(n=0) ^∞ (−1)^n (u^(n+1) /(n+1)) =Σ_(n=1) ^(∞ ) (−1)^(n−1 ) (u^n /n) ⇒ ln(1+e^(−x) )=Σ_(n=1) ^∞ (−1)^(n−1) (e^(−nx) /n) and ∫_0 ^∞ ln(1+e^(−x) )dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^∞ e^(−nx) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)(−(1/n))[e^(−nx) ]_0 ^∞ =−Σ_(n=1) ^∞ (((−1)^n )/n^2 )=−δ(2) =−(2^(1−2) −1)ξ(2) =−((1/2)−1)×(π^2 /6)=(π^2 /(12)) ln^′ (1−u)=−(1/(1−u))=−Σ_(n=0) ^∞ u^(n ) ⇒ ln(1−u)=−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (u^n /n) ⇒ln(1−e^(−x) ) =−Σ_(n=1) ^∞ (e^(−nx) /n) ⇒ ∫_0 ^∞ ln(1−e^(−x) )dx =−Σ_(n=1) ^∞ (1/n)∫_0 ^∞ e^(−nx) dx =−Σ_(n=1) ^∞ (1/n)[−(1/n)e^(−nx) ]_0 ^∞ =−Σ_(n=1) ^∞ (1/n^2 )=−(π^2 /6) ⇒ I=(π^2 /(12))+(π^2 /6)=((3π^2 )/(12))⇒I=(π^2 /4)](Q157188.png)
Answered by Mathspace last updated on 20/Oct/21
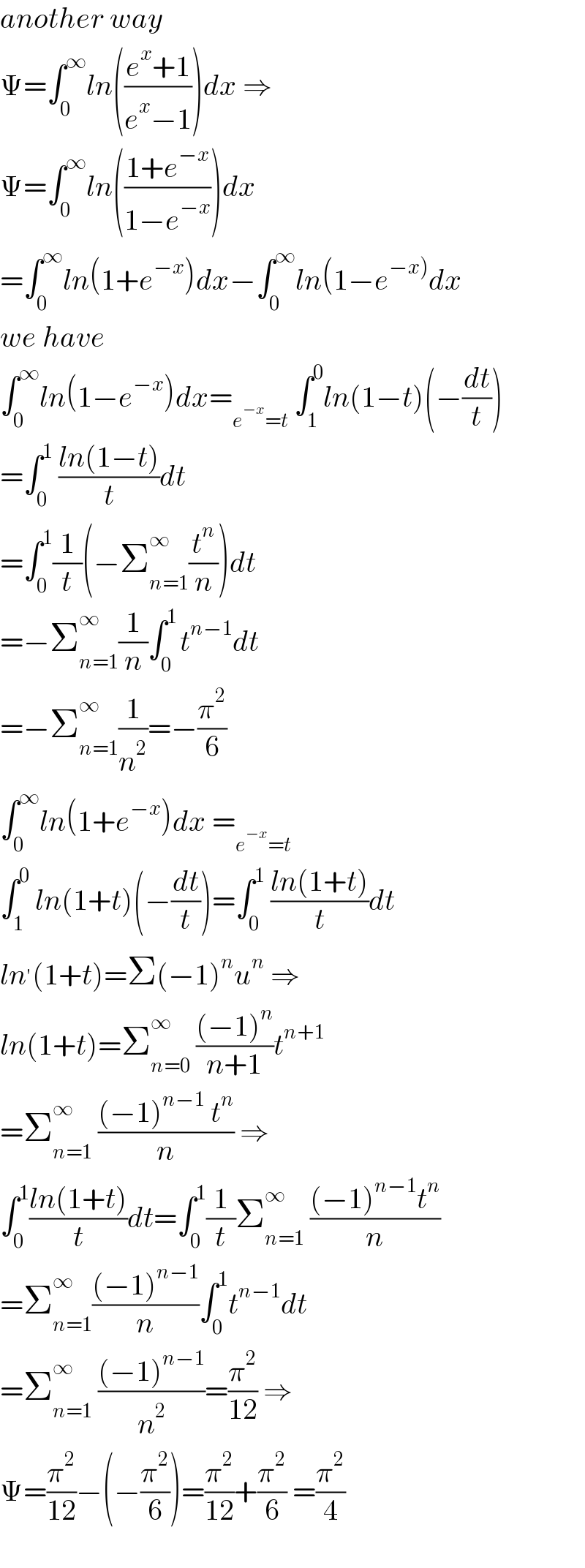
| ||
Question and Answers Forum | ||
Question Number 157175 by cortano last updated on 20/Oct/21 | ||
 | ||
Commented by puissant last updated on 20/Oct/21 | ||
 | ||
Answered by Mathspace last updated on 20/Oct/21 | ||
![I=∫_0 ^∞ ln(((1+e^(−x) )/(1−e^(−x) )))dx =∫_0 ^∞ ln(1+e^(−x) )dx−∫_0 ^∞ ln(1−e^(−x)) dx ln^′ (1+u)dx=(1/(1+u))=Σ(−1)^n u^n ⇒ ln(1+u)=Σ_(n=0) ^∞ (−1)^n (u^(n+1) /(n+1)) =Σ_(n=1) ^(∞ ) (−1)^(n−1 ) (u^n /n) ⇒ ln(1+e^(−x) )=Σ_(n=1) ^∞ (−1)^(n−1) (e^(−nx) /n) and ∫_0 ^∞ ln(1+e^(−x) )dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)∫_0 ^∞ e^(−nx) dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)(−(1/n))[e^(−nx) ]_0 ^∞ =−Σ_(n=1) ^∞ (((−1)^n )/n^2 )=−δ(2) =−(2^(1−2) −1)ξ(2) =−((1/2)−1)×(π^2 /6)=(π^2 /(12)) ln^′ (1−u)=−(1/(1−u))=−Σ_(n=0) ^∞ u^(n ) ⇒ ln(1−u)=−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (u^n /n) ⇒ln(1−e^(−x) ) =−Σ_(n=1) ^∞ (e^(−nx) /n) ⇒ ∫_0 ^∞ ln(1−e^(−x) )dx =−Σ_(n=1) ^∞ (1/n)∫_0 ^∞ e^(−nx) dx =−Σ_(n=1) ^∞ (1/n)[−(1/n)e^(−nx) ]_0 ^∞ =−Σ_(n=1) ^∞ (1/n^2 )=−(π^2 /6) ⇒ I=(π^2 /(12))+(π^2 /6)=((3π^2 )/(12))⇒I=(π^2 /4)](Q157188.png) | ||
| ||
Answered by Mathspace last updated on 20/Oct/21 | ||
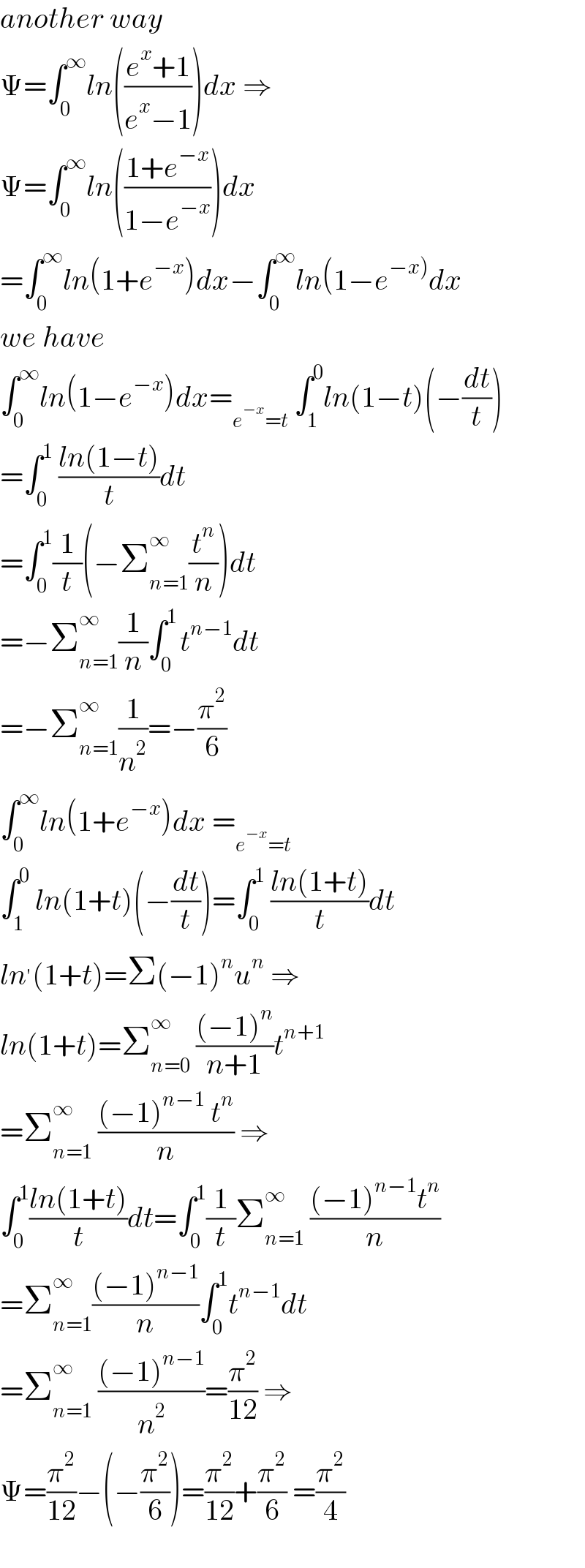 | ||
| ||