
Question and Answers Forum
Question Number 157216 by Khalmohmmad last updated on 21/Oct/21
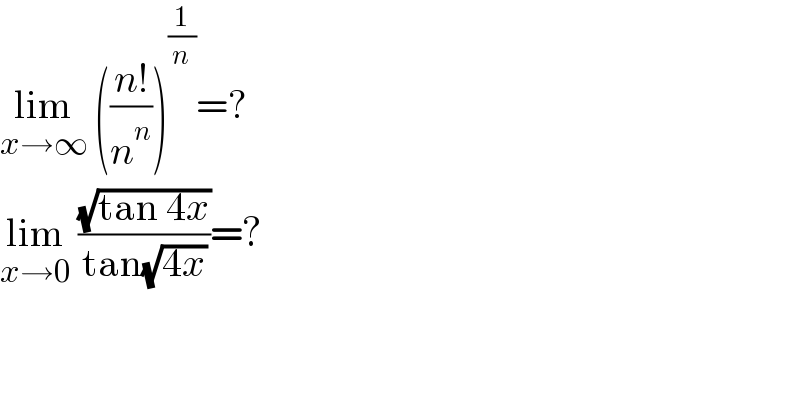
Commented by cortano last updated on 21/Oct/21
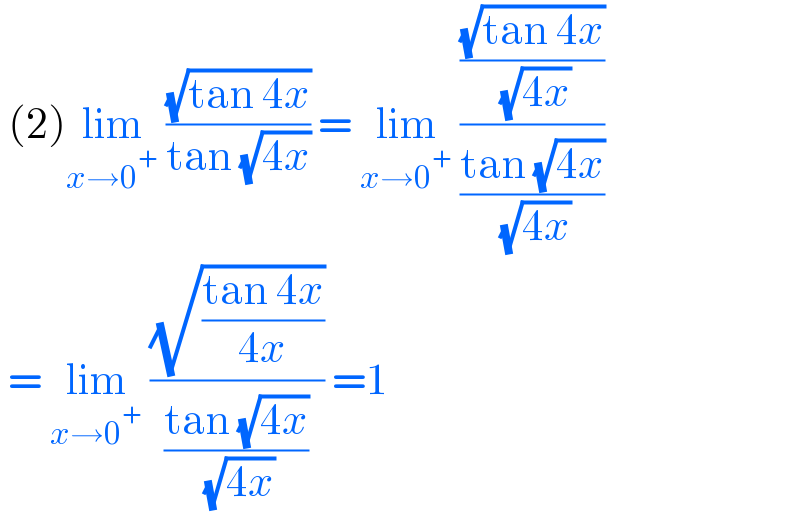
Answered by puissant last updated on 21/Oct/21
![1) L=lim_(n→∞) (((n!)/n^n ))^(1/n) ; ln(L)=lim_(n→∞) (1/n)ln(((n!)/n^n )) = lim_(n→∞) (1/n){ln(n!)−nln(n)} = lim_(n→∞) (1/n)Σ_(k=1) ^n {ln(k)−ln(n)} =lim_(n→∞) (1/n)Σ_(k=1) ^n ln((k/n)) = ∫_0 ^1 ln(x)dx IBP → { ((u=lnx)),((v′=1)) :} ⇒ { ((u′=(1/x))),((v=x)) :} ⇒ ln(L)=[xlnx]_0 ^1 −∫_0 ^1 1dx ⇒ ln(L)=−1 → L=e^(−1) =(1/e).. ∴∵ L=lim_(n→∞) (((n!)/n^n ))^(1/n) = (1/e).. ...........Le puissant............](Q157236.png)
| ||
Question and Answers Forum | ||
Question Number 157216 by Khalmohmmad last updated on 21/Oct/21 | ||
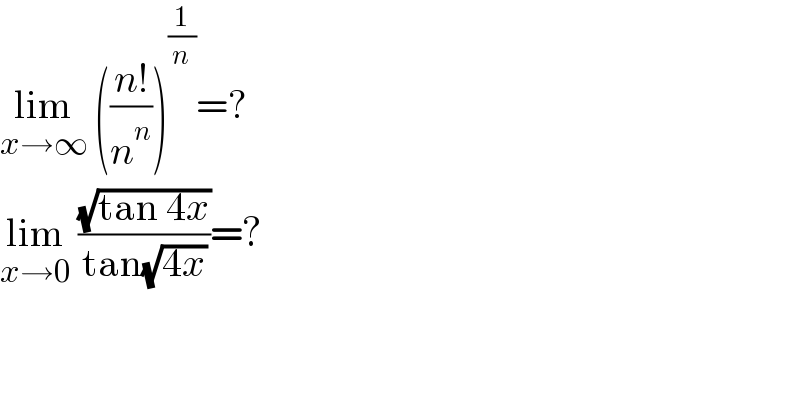 | ||
Commented by cortano last updated on 21/Oct/21 | ||
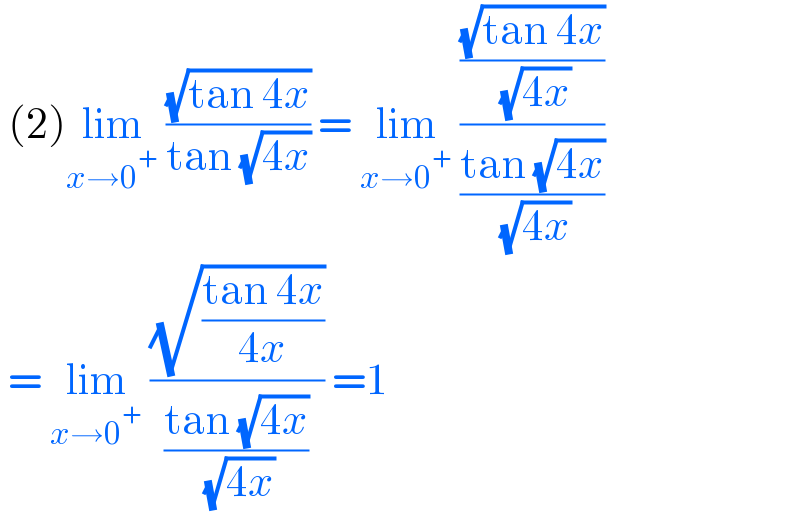 | ||
Answered by puissant last updated on 21/Oct/21 | ||
![1) L=lim_(n→∞) (((n!)/n^n ))^(1/n) ; ln(L)=lim_(n→∞) (1/n)ln(((n!)/n^n )) = lim_(n→∞) (1/n){ln(n!)−nln(n)} = lim_(n→∞) (1/n)Σ_(k=1) ^n {ln(k)−ln(n)} =lim_(n→∞) (1/n)Σ_(k=1) ^n ln((k/n)) = ∫_0 ^1 ln(x)dx IBP → { ((u=lnx)),((v′=1)) :} ⇒ { ((u′=(1/x))),((v=x)) :} ⇒ ln(L)=[xlnx]_0 ^1 −∫_0 ^1 1dx ⇒ ln(L)=−1 → L=e^(−1) =(1/e).. ∴∵ L=lim_(n→∞) (((n!)/n^n ))^(1/n) = (1/e).. ...........Le puissant............](Q157236.png) | ||
| ||