Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 15742 by RasheedSoomro last updated on 14/Jun/17

This question is posted on the request of mrW1 (See comments of my answer to Q#15543). Find the last last non-zero digit of the expansion of 2000!

$$\mathrm{This}\:\mathrm{question}\:\mathrm{is}\:\mathrm{posted}\:\mathrm{on}\:\mathrm{the}\:\mathrm{request}\:\mathrm{of}\:\mathrm{mrW1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left(\mathrm{See}\:\mathrm{comments}\:\mathrm{of}\:\mathrm{my}\:\mathrm{answer}\:\mathrm{to}\:\mathrm{Q}#\mathrm{15543}\right). \\ $$$$ \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{last}\:\mathrm{last}\:\:\boldsymbol{\mathrm{non}}-\boldsymbol{\mathrm{zero}}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{the}\:\mathrm{expansion} \\ $$$$\mathrm{of}\:\:\mathrm{2000}! \\ $$

Commented by mrW1 last updated on 13/Jun/17

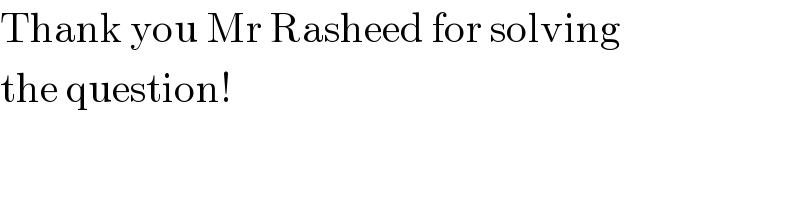
Thank you Mr Rasheed for solving the question!

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Mr}\:\mathrm{Rasheed}\:\mathrm{for}\:\mathrm{solving} \\ $$$$\mathrm{the}\:\mathrm{question}! \\ $$

Answered by RasheedSoomro last updated on 13/Jun/17

^• 2000! has as many ending zeros as many times 10 is factor of it. ^• 10 is as many times factor of 2000! as many times 5 is factor of of it. ^• 5 is ( ⌊((2000)/5)⌋+⌊((2000)/(25))⌋+⌊((2000)/(125))⌋+⌊((2000)/(625))⌋ ) =400+80+16+3=499 times factor of 2000! That all means 2000! has 499 ending 0′s and if p=((2000!)/(10^(499) )) then p has no ending 0. And how is this related to last non-zero digit of 2000! ? It′s as that Last non-zero digit of 2000!(say d) =unit digit of p=2000!/10^(499) Hence p≡d(mod 10) Now, 2000!=(1...4)(6...9)...(1996...1999)(5.10...2000) =5^(400) (1...4)(6...9)...(1996...1999)^(−400 brackets−) .400! 400!=(1...4)(6...9)...(396...399)(5.10...400) =5^(80) (1...4)(6...9)...(396...399)^(−80 brackets−) .80! 80!=(1...4)(6...9)...(76...79)(5.10..80) =5^(16) (1...4)(6...9)...(76...79)^(16 brackets) .16! 16!=(1...4)(6...9)(11...14)(16)(5.10.15) =5^3 (1...4)(6...9)(11...14){(16).3!} =5^3 (1...4)(6...9)(11...14)^(3 brackets) (96) Total 499 brackets(as many as there are zeros) 2000!=5^(499) {(1...4)(6...9)...(1996...1999)} ×{(1...4)(6...9)...(396...399)} ×{(1...4)(6...9)...(76...79)} ×{(1...4)(6...9)(11...14)}(96) p=((2000!)/(2^(499) .5^(499) ))=((1/2^(499) )){(1...4)(6...9)...(1996...1999)} ×{(1...4)(6...9)...(396...399)} ×{(1...4)(6...9)...(76...79)} ×{(1...4)(6...9)(11...14)}(96) p={(((1...4)/2))(((6...9)/2))...(((1996...1999)/2))} ×{(((1...4)/2))(((6...9)/2))...(((396...399)/2))} ×{(((1...4)/2))(((6...9)/2))...(((76...79)/2))} ×{(((1...4)/2))(((6...9)/2))(((11...14)/2))}(96) Now, we know that or can prove that (((5k+1)(5k+2)(5k+3)(5k+4))/2)≡2(mod 10)

$$\:^{\bullet} \mathrm{2000}!\:\:\mathrm{has}\:\mathrm{as}\:\mathrm{many}\:\mathrm{ending}\:\mathrm{zeros} \\ $$$$\:\:\:\:\mathrm{as}\:\:\mathrm{many}\:\mathrm{times}\:\mathrm{10}\:\mathrm{is}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{it}. \\ $$$$\:^{\bullet} \mathrm{10}\:\mathrm{is}\:\mathrm{as}\:\mathrm{many}\:\mathrm{times}\:\mathrm{factor}\:\mathrm{of}\:\mathrm{2000}! \\ $$$$\:\:\:\:\mathrm{as}\:\mathrm{many}\:\mathrm{times}\:\mathrm{5}\:\mathrm{is}\:\mathrm{factor}\:\mathrm{of}\:\:\mathrm{of}\:\:\mathrm{it}. \\ $$$$\:^{\bullet} \mathrm{5}\:\mathrm{is}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\:\lfloor\frac{\mathrm{2000}}{\mathrm{5}}\rfloor+\lfloor\frac{\mathrm{2000}}{\mathrm{25}}\rfloor+\lfloor\frac{\mathrm{2000}}{\mathrm{125}}\rfloor+\lfloor\frac{\mathrm{2000}}{\mathrm{625}}\rfloor\:\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:=\mathrm{400}+\mathrm{80}+\mathrm{16}+\mathrm{3}=\mathrm{499}\:\mathrm{times} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{factor}\:\mathrm{of}\:\:\mathrm{2000}! \\ $$$$\mathrm{That}\:\mathrm{all}\:\mathrm{means}\:\mathrm{2000}!\:\mathrm{has}\:\mathrm{499}\:\mathrm{ending}\:\:\mathrm{0}'\mathrm{s} \\ $$$$\mathrm{and}\:\mathrm{if}\:\mathrm{p}=\frac{\mathrm{2000}!}{\mathrm{10}^{\mathrm{499}} }\:\mathrm{then}\:\mathrm{p}\:\mathrm{has}\:\mathrm{no}\:\mathrm{ending}\:\mathrm{0}. \\ $$$$\mathrm{And}\:\mathrm{how}\:\mathrm{is}\:\mathrm{this}\:\mathrm{related}\:\mathrm{to}\:\boldsymbol{\mathrm{last}}\:\boldsymbol{\mathrm{non}}-\boldsymbol{\mathrm{zero}}\:\boldsymbol{\mathrm{digit}} \\ $$$$\boldsymbol{\mathrm{of}}\:\:\mathrm{2000}!\:\:? \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{as}\:\mathrm{that}\: \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{Last}}\:\boldsymbol{\mathrm{non}}-\boldsymbol{\mathrm{zero}}\:\boldsymbol{\mathrm{digit}}\:\boldsymbol{\mathrm{of}}\:\mathrm{2000}!\left(\mathrm{say}\:\mathrm{d}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{unit}}\:\boldsymbol{\mathrm{digit}}\:\boldsymbol{\mathrm{of}}\:\mathrm{p}=\mathrm{2000}!/\mathrm{10}^{\mathrm{499}} \\ $$$$\:\:\:\mathrm{Hence}\:\mathrm{p}\equiv\mathrm{d}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$ \\ $$$$\mathrm{Now}, \\ $$$$\:\:\:\:\:\mathrm{2000}!=\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{1996}...\mathrm{1999}\right)\left(\mathrm{5}.\mathrm{10}...\mathrm{2000}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}^{\mathrm{400}} \overset{−\mathrm{400}\:\mathrm{brackets}−} {\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{1996}...\mathrm{1999}\right)}.\mathrm{400}! \\ $$$$\:\:\:\:\:\:\mathrm{400}!=\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{396}...\mathrm{399}\right)\left(\mathrm{5}.\mathrm{10}...\mathrm{400}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}^{\mathrm{80}} \overset{−\mathrm{80}\:\mathrm{brackets}−} {\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{396}...\mathrm{399}\right)}.\mathrm{80}! \\ $$$$\:\:\:\:\:\mathrm{80}!=\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{76}...\mathrm{79}\right)\left(\mathrm{5}.\mathrm{10}..\mathrm{80}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}^{\mathrm{16}} \overset{\mathrm{16}\:\mathrm{brackets}} {\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{76}...\mathrm{79}\right)}.\mathrm{16}! \\ $$$$\:\:\:\:\mathrm{16}!=\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)\left(\mathrm{11}...\mathrm{14}\right)\left(\mathrm{16}\right)\left(\mathrm{5}.\mathrm{10}.\mathrm{15}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}^{\mathrm{3}} \left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)\left(\mathrm{11}...\mathrm{14}\right)\left\{\left(\mathrm{16}\right).\mathrm{3}!\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}^{\mathrm{3}} \overset{\mathrm{3}\:\mathrm{brackets}} {\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)\left(\mathrm{11}...\mathrm{14}\right)}\left(\mathrm{96}\right) \\ $$$$\mathrm{Total}\:\mathrm{499}\:\mathrm{brackets}\left(\mathrm{as}\:\mathrm{many}\:\mathrm{as}\:\mathrm{there}\:\mathrm{are}\:\mathrm{zeros}\right) \\ $$$$\mathrm{2000}!=\mathrm{5}^{\mathrm{499}} \left\{\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{1996}...\mathrm{1999}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{396}...\mathrm{399}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{76}...\mathrm{79}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)\left(\mathrm{11}...\mathrm{14}\right)\right\}\left(\mathrm{96}\right) \\ $$$$\:\:\mathrm{p}=\frac{\mathrm{2000}!}{\mathrm{2}^{\mathrm{499}} .\mathrm{5}^{\mathrm{499}} }=\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{499}} }\right)\left\{\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{1996}...\mathrm{1999}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{396}...\mathrm{399}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)...\left(\mathrm{76}...\mathrm{79}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\mathrm{1}...\mathrm{4}\right)\left(\mathrm{6}...\mathrm{9}\right)\left(\mathrm{11}...\mathrm{14}\right)\right\}\left(\mathrm{96}\right) \\ $$$$\:\mathrm{p}=\left\{\left(\frac{\mathrm{1}...\mathrm{4}}{\mathrm{2}}\right)\left(\frac{\mathrm{6}...\mathrm{9}}{\mathrm{2}}\right)...\left(\frac{\mathrm{1996}...\mathrm{1999}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\frac{\mathrm{1}...\mathrm{4}}{\mathrm{2}}\right)\left(\frac{\mathrm{6}...\mathrm{9}}{\mathrm{2}}\right)...\left(\frac{\mathrm{396}...\mathrm{399}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\frac{\mathrm{1}...\mathrm{4}}{\mathrm{2}}\right)\left(\frac{\mathrm{6}...\mathrm{9}}{\mathrm{2}}\right)...\left(\frac{\mathrm{76}...\mathrm{79}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\left\{\left(\frac{\mathrm{1}...\mathrm{4}}{\mathrm{2}}\right)\left(\frac{\mathrm{6}...\mathrm{9}}{\mathrm{2}}\right)\left(\frac{\mathrm{11}...\mathrm{14}}{\mathrm{2}}\right)\right\}\left(\mathrm{96}\right) \\ $$$$\:\:\mathrm{Now},\:\:\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{or}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\left(\mathrm{5k}+\mathrm{1}\right)\left(\mathrm{5k}+\mathrm{2}\right)\left(\mathrm{5k}+\mathrm{3}\right)\left(\mathrm{5k}+\mathrm{4}\right)}{\mathrm{2}}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$

Commented by Tinkutara last updated on 13/Jun/17

We have last non-zero digit of n! = 2^A × A! × B! where A = [(n/5)] and B = remainder when n is divided by 5. Last non-zero digit of 2000! = 2^(400) × 400! × 0! = 2^(400) × 400! Last non-zero digit of 400! = 2^(80) × 80! Last non-zero digit of 80! = 2^(16) × 16! Last non-zero digit of 16! = 2^3 × 3! × 1! = 48 ≡ 8 Last non-zero digit of 2000! ≡ 6 × 400! = 6 × 6 × 80! ≡ 6 × 80! ≡ 6 × 6 × 16! ≡ 6 × 16! ≡ 6 × 8 ≡ 8 Similarly last non-zero digit of 1000! = 2^(200) × 200! Last non-zero digit of 200! = 2^(40) × 40! Last non-zero digit of 40! = 2^8 × 8! Last non-zero digit of 8! = 2^1 × 1! × 3! = 2 × 6 ≡ 2 Last non-zero digit of 1000! = 6 × 200! = 6 × 6 × 6 × 2 ≡ 2

$$\mathrm{We}\:\mathrm{have}\:\mathrm{last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:{n}! \\ $$$$=\:\mathrm{2}^{\mathrm{A}} \:×\:\mathrm{A}!\:×\:\mathrm{B}! \\ $$$$\mathrm{where}\:\mathrm{A}\:=\:\left[\frac{{n}}{\mathrm{5}}\right]\:\mathrm{and}\:\mathrm{B}\:=\:\mathrm{remainder} \\ $$$$\mathrm{when}\:{n}\:\mathrm{is}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{5}. \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{2000}! \\ $$$$=\:\mathrm{2}^{\mathrm{400}} \:×\:\mathrm{400}!\:×\:\mathrm{0}!\:=\:\mathrm{2}^{\mathrm{400}} \:×\:\mathrm{400}! \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{400}! \\ $$$$=\:\mathrm{2}^{\mathrm{80}} \:×\:\mathrm{80}! \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{80}! \\ $$$$=\:\mathrm{2}^{\mathrm{16}} \:×\:\mathrm{16}! \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{16}! \\ $$$$=\:\mathrm{2}^{\mathrm{3}} \:×\:\mathrm{3}!\:×\:\mathrm{1}!\:=\:\mathrm{48}\:\equiv\:\mathrm{8} \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{2000}! \\ $$$$\equiv\:\mathrm{6}\:×\:\mathrm{400}!\:=\:\mathrm{6}\:×\:\mathrm{6}\:×\:\mathrm{80}!\:\equiv\:\mathrm{6}\:×\:\mathrm{80}! \\ $$$$\equiv\:\mathrm{6}\:×\:\mathrm{6}\:×\:\mathrm{16}!\:\equiv\:\mathrm{6}\:×\:\mathrm{16}!\:\equiv\:\mathrm{6}\:×\:\mathrm{8}\:\equiv\:\mathrm{8} \\ $$$$\mathrm{Similarly}\:\mathrm{last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{1000}! \\ $$$$=\:\mathrm{2}^{\mathrm{200}} \:×\:\mathrm{200}! \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{200}! \\ $$$$=\:\mathrm{2}^{\mathrm{40}} \:×\:\mathrm{40}! \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{40}! \\ $$$$=\:\mathrm{2}^{\mathrm{8}} \:×\:\mathrm{8}! \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{8}! \\ $$$$=\:\mathrm{2}^{\mathrm{1}} \:×\:\mathrm{1}!\:×\:\mathrm{3}!\:=\:\mathrm{2}\:×\:\mathrm{6}\:\equiv\:\mathrm{2} \\ $$$$\mathrm{Last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{1000}! \\ $$$$=\:\mathrm{6}\:×\:\mathrm{200}!\:=\:\mathrm{6}\:×\:\mathrm{6}\:×\:\mathrm{6}\:×\:\mathrm{2}\:\equiv\:\mathrm{2} \\ $$

Commented by RasheedSoomro last updated on 13/Jun/17

I don′t know that formula!

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{that}\:\mathrm{formula}! \\ $$

Commented by RasheedSoomro last updated on 13/Jun/17

Continue from my above answer Sorry that there was no space and my few lines couldn′t be included in the above answer. I write them below So each bracket is congruentto 2(mod 10): ((∗.∗.∗.∗)/2)≡2(mod 10) [499 congruences).....(i) 96≡6(mod 10).......................................(ii) (i)×(ii): p≡2^(499) .6(mod 10) p≡8.6(mod 10) [∵ 2^(4k+3) ≡8]] p≡8(mod 10) Hence the last non-zero digit of 2000!=8

$$\mathrm{Continue}\:\mathrm{from}\:\mathrm{my}\:\:\mathrm{above}\:\mathrm{answer} \\ $$$$\mathrm{Sorry}\:\mathrm{that}\:\mathrm{there}\:\mathrm{was}\:\mathrm{no}\:\mathrm{space}\:\mathrm{and}\:\mathrm{my}\:\mathrm{few}\:\mathrm{lines}\: \\ $$$$\mathrm{couldn}'\mathrm{t}\:\mathrm{be}\:\mathrm{included}\:\mathrm{in}\:\mathrm{the}\:\mathrm{above}\:\mathrm{answer}. \\ $$$$\mathrm{I}\:\mathrm{write}\:\mathrm{them}\:\mathrm{below} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{So}\:\mathrm{each}\:\mathrm{bracket}\:\mathrm{is}\:\mathrm{congruentto}\:\mathrm{2}\left(\mathrm{mod}\:\mathrm{10}\right): \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{\ast.\ast.\ast.\ast}{\mathrm{2}}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{10}\right)\:\:\:\left[\mathrm{499}\:\mathrm{congruences}\right).....\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{96}\equiv\mathrm{6}\left(\mathrm{mod}\:\mathrm{10}\right).......................................\left(\mathrm{ii}\right) \\ $$$$\:\left(\mathrm{i}\right)×\left(\mathrm{ii}\right):\:\:\mathrm{p}\equiv\mathrm{2}^{\mathrm{499}} .\mathrm{6}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\left.\:\:\:\:\:\:\:\:\mathrm{p}\equiv\mathrm{8}.\mathrm{6}\left(\mathrm{mod}\:\mathrm{10}\right)\:\:\:\left[\because\:\mathrm{2}^{\mathrm{4k}+\mathrm{3}} \equiv\mathrm{8}\right]\right] \\ $$$$\:\:\:\:\:\:\:\:\mathrm{p}\equiv\mathrm{8}\left(\mathrm{mod}\:\mathrm{10}\right)\:\:\: \\ $$$$\mathrm{Hence}\:\mathrm{the}\:\mathrm{last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{2000}!=\mathrm{8} \\ $$

Commented by mrW1 last updated on 13/Jun/17

Great job done!

$$\mathrm{Great}\:\mathrm{job}\:\mathrm{done}! \\ $$

Commented by mrW1 last updated on 13/Jun/17

To tinkutara: Your solution is fantastic! How did you get the solution? Is it a method developed by yourself? Can you supply more details about the method?

$$\mathrm{To}\:\mathrm{tinkutara}: \\ $$$$\mathrm{Your}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{fantastic}! \\ $$$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{solution}?\:\mathrm{Is}\:\mathrm{it}\:\mathrm{a} \\ $$$$\mathrm{method}\:\mathrm{developed}\:\mathrm{by}\:\mathrm{yourself}?\:\mathrm{Can} \\ $$$$\mathrm{you}\:\mathrm{supply}\:\mathrm{more}\:\mathrm{details}\:\mathrm{about}\:\mathrm{the} \\ $$$$\mathrm{method}? \\ $$

Commented by Tinkutara last updated on 14/Jun/17

I checked the method on internet. You can type “last non-zero digit of a factorial” on Google to get the formula but I don′t know its proof.

$$\mathrm{I}\:\mathrm{checked}\:\mathrm{the}\:\mathrm{method}\:\mathrm{on}\:\mathrm{internet}.\:\mathrm{You} \\ $$$$\mathrm{can}\:\mathrm{type}\:``\mathrm{last}\:\mathrm{non}-\mathrm{zero}\:\mathrm{digit}\:\mathrm{of}\:\mathrm{a} \\ $$$$\mathrm{factorial}''\:\mathrm{on}\:\mathrm{Google}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{formula} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{its}\:\mathrm{proof}. \\ $$

Commented by mrW1 last updated on 14/Jun/17

thanks!

$$\mathrm{thanks}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com