
Question and Answers Forum
Question Number 157442 by bobhans last updated on 23/Oct/21
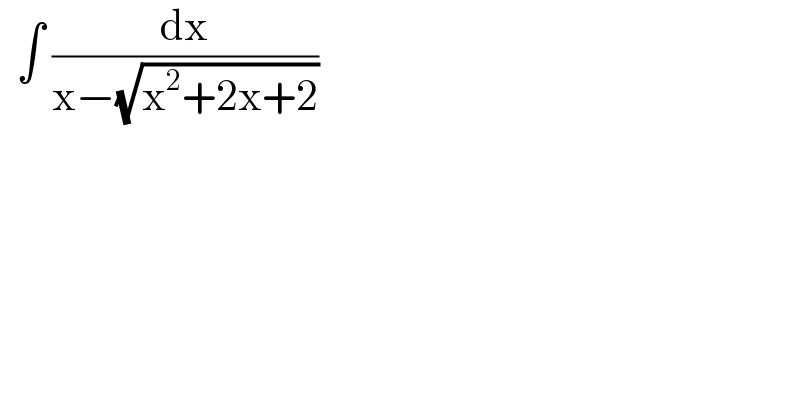
Answered by MJS_new last updated on 23/Oct/21
![∫(dx/(x−(√(x^2 +2x+2))))= [t=x+1+(√(x^2 +2x+2)) → dx=((√(x^2 +2x+2))/(x+1+(√(x^2 +2x+2))))dt] =−(1/2)∫((t^2 +1)/(t(t+1)))dt=∫((1/(t+1))−(1/(2t))−(1/2))dt= =ln (t+1) −(1/2)ln t −(1/2)t= =(1/2)(ln (((t+1)^2 )/t) −t)= =(1/2)(ln (1+(√(x^2 +2x+2))) −x−(√(x^2 +2x+2)))+C](Q157447.png)
Answered by cortano last updated on 23/Oct/21

| ||
Question and Answers Forum | ||
Question Number 157442 by bobhans last updated on 23/Oct/21 | ||
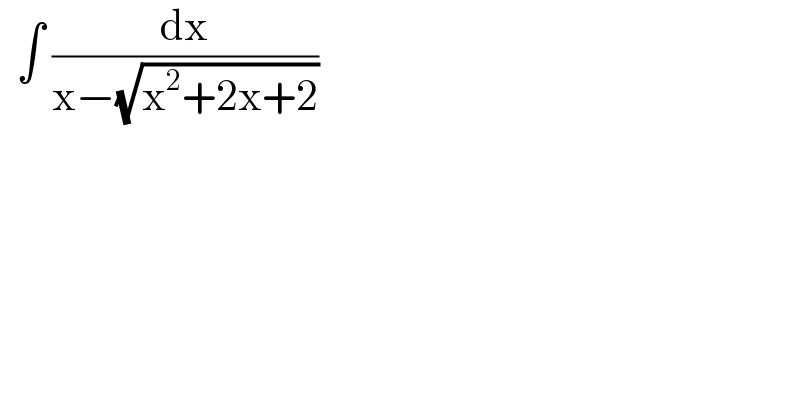 | ||
Answered by MJS_new last updated on 23/Oct/21 | ||
![∫(dx/(x−(√(x^2 +2x+2))))= [t=x+1+(√(x^2 +2x+2)) → dx=((√(x^2 +2x+2))/(x+1+(√(x^2 +2x+2))))dt] =−(1/2)∫((t^2 +1)/(t(t+1)))dt=∫((1/(t+1))−(1/(2t))−(1/2))dt= =ln (t+1) −(1/2)ln t −(1/2)t= =(1/2)(ln (((t+1)^2 )/t) −t)= =(1/2)(ln (1+(√(x^2 +2x+2))) −x−(√(x^2 +2x+2)))+C](Q157447.png) | ||
| ||
Answered by cortano last updated on 23/Oct/21 | ||
 | ||
| ||