Question Number 157457 by MathSh last updated on 23/Oct/21
$$\mathrm{xy}^{'} \:+\:\mathrm{y}\:=\:\mathrm{y}^{\mathrm{2}} \:\mathrm{ln}\:\mathrm{x} \\ $$$$ \\ $$
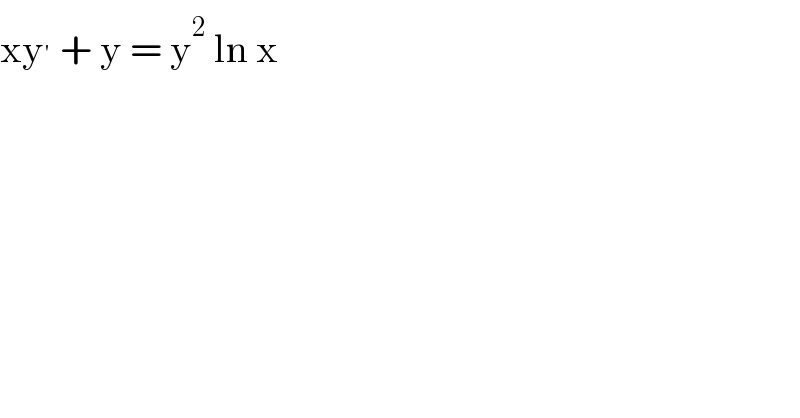
Answered by ajfour last updated on 23/Oct/21
$${xdy}+{ydx}={y}^{\mathrm{2}} \left(\mathrm{ln}\:{x}\right){dx} \\ $$$$\frac{{xdy}}{{y}^{\mathrm{2}} }+\frac{{ydx}}{{y}^{\mathrm{2}} }=\left(\mathrm{ln}\:{x}\right){dx} \\ $$$$\frac{{d}\left({xy}\right)}{\left({xy}\right)^{\mathrm{2}} }=\frac{\left(\mathrm{ln}\:{x}\right){dx}}{{x}^{\mathrm{2}} } \\ $$$${let}\:\:{xy}={s}\:;\:\:\mathrm{ln}\:{x}={t} \\ $$$$\Rightarrow\:\:\frac{{ds}}{{s}^{\mathrm{2}} }=\frac{{tdt}}{{e}^{{t}} } \\ $$$$−\frac{\mathrm{1}}{{s}}+{c}={e}^{−{t}} {tdt}\:=\:{f}\left({t}\right){dt} \\ $$$$\:\:{I}=\int{e}^{−{t}} {tdt} \\ $$$$\:\:\:\:=−{te}^{−{t}} −{e}^{−{t}} \\ $$$${hence} \\ $$$$\:\:\frac{\mathrm{1}}{{xy}}=\frac{\mathrm{ln}\:{x}+\mathrm{1}}{{x}}+{c} \\ $$$$\frac{\mathrm{1}}{{y}}=\mathrm{ln}\:{x}+{cx}+\mathrm{1} \\ $$$$ \\ $$
Commented by MathSh last updated on 23/Oct/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\boldsymbol{\mathrm{Ser}} \\ $$
Answered by mnjuly1970 last updated on 23/Oct/21
![y′+(y/x)= (y^( 2) /x) ln(x) y^(−1) =u ⇒ −y^( −2) y′=u′ −y^( −2) y′ −y^(−1) (1/x) = −(1/x) ln(x) u′ −(u/(x )) = −((ln(x))/x) u= e^( ∫(1/x) dx) ( ∫−((ln(x))/x) e^( −∫(1/x)dx) dx +C) = x ( ∫−((ln(x))/x^( 2) )dx +C) = x [ ((ln( x ))/x) − ∫(1/x^( 2) ) dx +C ] = ln(x) +1 + C x y = (1/(ln(x)+1+Cx))](Q157482.png)
$$\:\:\:{y}'+\frac{{y}}{{x}}=\:\frac{{y}^{\:\mathrm{2}} }{{x}}\:{ln}\left({x}\right) \\ $$$$\:\:\:\:\:{y}^{−\mathrm{1}} ={u}\:\Rightarrow\:−{y}^{\:−\mathrm{2}} {y}'={u}' \\ $$$$\:\:\:\:−{y}^{\:−\mathrm{2}} {y}'\:−{y}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\:=\:−\frac{\mathrm{1}}{{x}}\:{ln}\left({x}\right) \\ $$$$\:\:\:\:\:{u}'\:−\frac{{u}}{{x}\:}\:=\:−\frac{{ln}\left({x}\right)}{{x}} \\ $$$$\:\:\:\:\:\:\:{u}=\:{e}^{\:\int\frac{\mathrm{1}}{{x}}\:{dx}} \left(\:\int−\frac{{ln}\left({x}\right)}{{x}}\:{e}^{\:−\int\frac{\mathrm{1}}{{x}}{dx}} {dx}\:+{C}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:{x}\:\left(\:\int−\frac{{ln}\left({x}\right)}{{x}^{\:\mathrm{2}} }{dx}\:+{C}\right) \\ $$$$\:\:\:\:\:\:\:\:=\:{x}\:\left[\:\frac{{ln}\left(\:{x}\:\right)}{{x}}\:−\:\int\frac{\mathrm{1}}{{x}^{\:\mathrm{2}} }\:{dx}\:+{C}\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\:{ln}\left({x}\right)\:+\mathrm{1}\:+\:{C}\:{x} \\ $$$$\:\:\:\:\:\:{y}\:=\:\frac{\mathrm{1}}{{ln}\left({x}\right)+\mathrm{1}+{Cx}} \\ $$
Commented by MathSh last updated on 23/Oct/21
$$\mathrm{Tthank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\boldsymbol{\mathrm{Ser}} \\ $$
Commented by mnjuly1970 last updated on 23/Oct/21
$$\:\:{you}\:{are}\:{welcome}\:{sir} \\ $$
Answered by CAIMAN last updated on 23/Oct/21
Commented by MathSh last updated on 23/Oct/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$