Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 15759 by prakash jain last updated on 13/Jun/17

Let us call complex triangle which has either sides or angles are complex numbers. Let a,b,c ∈R which are sides of a complex triangle which need not satisfy triangle inequality. say a=1,b=2 and c=4. Prove (or counter example) (a/(sin A))=(b/(sin B))=(c/(sin C)) Is A+B+C=π? Assume only principle solution for A,B and C. For such a triangle A,B and C will take complex values.

$$\mathrm{Let}\:\mathrm{us}\:\mathrm{call}\:\mathrm{complex}\:\mathrm{triangle}\:\mathrm{which} \\ $$$$\mathrm{has}\:\mathrm{either}\:\mathrm{sides}\:\mathrm{or}\:\mathrm{angles}\:\mathrm{are} \\ $$$$\mathrm{complex}\:\mathrm{numbers}. \\ $$$$\mathrm{Let}\:{a},{b},{c}\:\in\mathbb{R}\:\mathrm{which}\:\mathrm{are}\:\mathrm{sides}\:\mathrm{of} \\ $$$$\mathrm{a}\:\mathrm{complex}\:\mathrm{triangle}\:\mathrm{which}\:\mathrm{need} \\ $$$$\mathrm{not}\:\mathrm{satisfy}\:\mathrm{triangle}\:\mathrm{inequality}. \\ $$$$\mathrm{say}\:{a}=\mathrm{1},{b}=\mathrm{2}\:\mathrm{and}\:{c}=\mathrm{4}. \\ $$$$\mathrm{Prove}\:\left(\mathrm{or}\:\mathrm{counter}\:\mathrm{example}\right) \\ $$$$\frac{{a}}{\mathrm{sin}\:{A}}=\frac{{b}}{\mathrm{sin}\:{B}}=\frac{{c}}{\mathrm{sin}\:{C}} \\ $$$$\mathrm{Is}\:{A}+{B}+{C}=\pi? \\ $$$$\mathrm{Assume}\:\mathrm{only}\:\mathrm{principle}\:\mathrm{solution} \\ $$$$\mathrm{for}\:{A},{B}\:\mathrm{and}\:{C}. \\ $$$$\mathrm{For}\:\mathrm{such}\:\mathrm{a}\:\mathrm{triangle}\:{A},{B}\:\mathrm{and}\:{C} \\ $$$$\mathrm{will}\:\mathrm{take}\:\mathrm{complex}\:\mathrm{values}. \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Jun/17

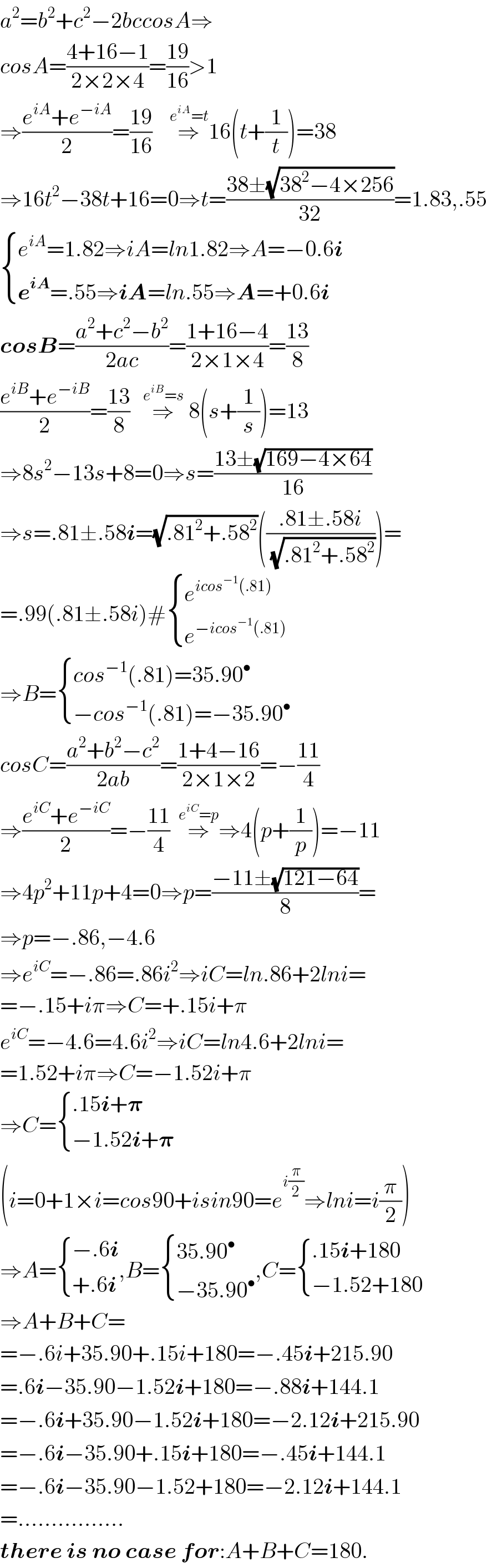
a^2 =b^2 +c^2 −2bccosA⇒ cosA=((4+16−1)/(2×2×4))=((19)/(16))>1 ⇒((e^(iA) +e^(−iA) )/2)=((19)/(16)) ⇒^(e^(iA) =t) 16(t+(1/t))=38 ⇒16t^2 −38t+16=0⇒t=((38±(√(38^2 −4×256)))/(32))=1.83,.55 { ((e^(iA) =1.82⇒iA=ln1.82⇒A=−0.6i)),((e^(iA) =.55⇒iA=ln.55⇒A=+0.6i)) :} cosB=((a^2 +c^2 −b^2 )/(2ac))=((1+16−4)/(2×1×4))=((13)/8) ((e^(iB) +e^(−iB) )/2)=((13)/8) ⇒^(e^(iB) =s) 8(s+(1/s))=13 ⇒8s^2 −13s+8=0⇒s=((13±(√(169−4×64)))/(16)) ⇒s=.81±.58i=(√(.81^2 +.58^2 ))(((.81±.58i)/(√(.81^2 +.58^2 ))))= =.99(.81±.58i)# { (e^(icos^(−1) (.81)) ),(e^(−icos^(−1) (.81)) ) :} ⇒B= { ((cos^(−1) (.81)=35.90^• )),((−cos^(−1) (.81)=−35.90^• )) :} cosC=((a^2 +b^2 −c^2 )/(2ab))=((1+4−16)/(2×1×2))=−((11)/4) ⇒((e^(iC) +e^(−iC) )/2)=−((11)/4) ⇒^(e^(iC) =p) ⇒4(p+(1/p))=−11 ⇒4p^2 +11p+4=0⇒p=((−11±(√(121−64)))/8)= ⇒p=−.86,−4.6 ⇒e^(iC) =−.86=.86i^2 ⇒iC=ln.86+2lni= =−.15+iπ⇒C=+.15i+π e^(iC) =−4.6=4.6i^2 ⇒iC=ln4.6+2lni= =1.52+iπ⇒C=−1.52i+π ⇒C= { ((.15i+𝛑)),((−1.52i+𝛑)) :} (i=0+1×i=cos90+isin90=e^(i(π/2)) ⇒lni=i(π/2)) ⇒A= { ((−.6i)),((+.6i)) :},B= { ((35.90^• )),((−35.90^• )) :},C= { ((.15i+180)),((−1.52+180)) :} ⇒A+B+C= =−.6i+35.90+.15i+180=−.45i+215.90 =.6i−35.90−1.52i+180=−.88i+144.1 =−.6i+35.90−1.52i+180=−2.12i+215.90 =−.6i−35.90+.15i+180=−.45i+144.1 =−.6i−35.90−1.52+180=−2.12i+144.1 =................ there is no case for:A+B+C=180.

$${a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bccosA}\Rightarrow \\ $$$${cosA}=\frac{\mathrm{4}+\mathrm{16}−\mathrm{1}}{\mathrm{2}×\mathrm{2}×\mathrm{4}}=\frac{\mathrm{19}}{\mathrm{16}}>\mathrm{1} \\ $$$$\Rightarrow\frac{{e}^{{iA}} +{e}^{−{iA}} }{\mathrm{2}}=\frac{\mathrm{19}}{\mathrm{16}}\:\:\:\:\overset{{e}^{{iA}} ={t}} {\Rightarrow}\mathrm{16}\left({t}+\frac{\mathrm{1}}{{t}}\right)=\mathrm{38} \\ $$$$\Rightarrow\mathrm{16}{t}^{\mathrm{2}} −\mathrm{38}{t}+\mathrm{16}=\mathrm{0}\Rightarrow{t}=\frac{\mathrm{38}\pm\sqrt{\mathrm{38}^{\mathrm{2}} −\mathrm{4}×\mathrm{256}}}{\mathrm{32}}=\mathrm{1}.\mathrm{83},.\mathrm{55} \\ $$$$\begin{cases}{{e}^{{iA}} =\mathrm{1}.\mathrm{82}\Rightarrow{iA}={ln}\mathrm{1}.\mathrm{82}\Rightarrow{A}=−\mathrm{0}.\mathrm{6}\boldsymbol{{i}}}\\{\boldsymbol{{e}}^{\boldsymbol{{iA}}} =.\mathrm{55}\Rightarrow\boldsymbol{{iA}}={ln}.\mathrm{55}\Rightarrow\boldsymbol{{A}}=+\mathrm{0}.\mathrm{6}\boldsymbol{{i}}}\end{cases} \\ $$$$\boldsymbol{{cosB}}=\frac{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ac}}=\frac{\mathrm{1}+\mathrm{16}−\mathrm{4}}{\mathrm{2}×\mathrm{1}×\mathrm{4}}=\frac{\mathrm{13}}{\mathrm{8}} \\ $$$$\frac{{e}^{{iB}} +{e}^{−{iB}} }{\mathrm{2}}=\frac{\mathrm{13}}{\mathrm{8}}\:\:\:\overset{{e}^{{iB}} ={s}} {\Rightarrow}\:\mathrm{8}\left({s}+\frac{\mathrm{1}}{{s}}\right)=\mathrm{13} \\ $$$$\Rightarrow\mathrm{8}{s}^{\mathrm{2}} −\mathrm{13}{s}+\mathrm{8}=\mathrm{0}\Rightarrow{s}=\frac{\mathrm{13}\pm\sqrt{\mathrm{169}−\mathrm{4}×\mathrm{64}}}{\mathrm{16}} \\ $$$$\Rightarrow{s}=.\mathrm{81}\pm.\mathrm{58}\boldsymbol{{i}}=\sqrt{.\mathrm{81}^{\mathrm{2}} +.\mathrm{58}^{\mathrm{2}} }\left(\frac{.\mathrm{81}\pm.\mathrm{58}{i}}{\sqrt{.\mathrm{81}^{\mathrm{2}} +.\mathrm{58}^{\mathrm{2}} }}\right)= \\ $$$$=.\mathrm{99}\left(.\mathrm{81}\pm.\mathrm{58}{i}\right)#\begin{cases}{{e}^{{icos}^{−\mathrm{1}} \left(.\mathrm{81}\right)} }\\{{e}^{−{icos}^{−\mathrm{1}} \left(.\mathrm{81}\right)} }\end{cases} \\ $$$$\Rightarrow{B}=\begin{cases}{{cos}^{−\mathrm{1}} \left(.\mathrm{81}\right)=\mathrm{35}.\mathrm{90}^{\bullet} }\\{−{cos}^{−\mathrm{1}} \left(.\mathrm{81}\right)=−\mathrm{35}.\mathrm{90}^{\bullet} }\end{cases} \\ $$$${cosC}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}=\frac{\mathrm{1}+\mathrm{4}−\mathrm{16}}{\mathrm{2}×\mathrm{1}×\mathrm{2}}=−\frac{\mathrm{11}}{\mathrm{4}} \\ $$$$\Rightarrow\frac{{e}^{{iC}} +{e}^{−{iC}} }{\mathrm{2}}=−\frac{\mathrm{11}}{\mathrm{4}}\:\:\overset{{e}^{{iC}} ={p}} {\Rightarrow}\Rightarrow\mathrm{4}\left({p}+\frac{\mathrm{1}}{{p}}\right)=−\mathrm{11} \\ $$$$\Rightarrow\mathrm{4}{p}^{\mathrm{2}} +\mathrm{11}{p}+\mathrm{4}=\mathrm{0}\Rightarrow{p}=\frac{−\mathrm{11}\pm\sqrt{\mathrm{121}−\mathrm{64}}}{\mathrm{8}}= \\ $$$$\Rightarrow{p}=−.\mathrm{86},−\mathrm{4}.\mathrm{6} \\ $$$$\Rightarrow{e}^{{iC}} =−.\mathrm{86}=.\mathrm{86}{i}^{\mathrm{2}} \Rightarrow{iC}={ln}.\mathrm{86}+\mathrm{2}{lni}= \\ $$$$=−.\mathrm{15}+{i}\pi\Rightarrow{C}=+.\mathrm{15}{i}+\pi \\ $$$${e}^{{iC}} =−\mathrm{4}.\mathrm{6}=\mathrm{4}.\mathrm{6}{i}^{\mathrm{2}} \Rightarrow{iC}={ln}\mathrm{4}.\mathrm{6}+\mathrm{2}{lni}= \\ $$$$=\mathrm{1}.\mathrm{52}+{i}\pi\Rightarrow{C}=−\mathrm{1}.\mathrm{52}{i}+\pi \\ $$$$\Rightarrow{C}=\begin{cases}{.\mathrm{15}\boldsymbol{{i}}+\boldsymbol{\pi}}\\{−\mathrm{1}.\mathrm{52}\boldsymbol{{i}}+\boldsymbol{\pi}}\end{cases} \\ $$$$\left({i}=\mathrm{0}+\mathrm{1}×{i}={cos}\mathrm{90}+{isin}\mathrm{90}={e}^{{i}\frac{\pi}{\mathrm{2}}} \Rightarrow{lni}={i}\frac{\pi}{\mathrm{2}}\right) \\ $$$$\Rightarrow{A}=\begin{cases}{−.\mathrm{6}\boldsymbol{{i}}}\\{+.\mathrm{6}\boldsymbol{{i}}}\end{cases},{B}=\begin{cases}{\mathrm{35}.\mathrm{90}^{\bullet} }\\{−\mathrm{35}.\mathrm{90}^{\bullet} }\end{cases},{C}=\begin{cases}{.\mathrm{15}\boldsymbol{{i}}+\mathrm{180}}\\{−\mathrm{1}.\mathrm{52}+\mathrm{180}}\end{cases} \\ $$$$\Rightarrow{A}+{B}+{C}= \\ $$$$=−.\mathrm{6}{i}+\mathrm{35}.\mathrm{90}+.\mathrm{15}{i}+\mathrm{180}=−.\mathrm{45}\boldsymbol{{i}}+\mathrm{215}.\mathrm{90} \\ $$$$=.\mathrm{6}\boldsymbol{{i}}−\mathrm{35}.\mathrm{90}−\mathrm{1}.\mathrm{52}\boldsymbol{{i}}+\mathrm{180}=−.\mathrm{88}\boldsymbol{{i}}+\mathrm{144}.\mathrm{1} \\ $$$$=−.\mathrm{6}\boldsymbol{{i}}+\mathrm{35}.\mathrm{90}−\mathrm{1}.\mathrm{52}\boldsymbol{{i}}+\mathrm{180}=−\mathrm{2}.\mathrm{12}\boldsymbol{{i}}+\mathrm{215}.\mathrm{90} \\ $$$$=−.\mathrm{6}\boldsymbol{{i}}−\mathrm{35}.\mathrm{90}+.\mathrm{15}\boldsymbol{{i}}+\mathrm{180}=−.\mathrm{45}\boldsymbol{{i}}+\mathrm{144}.\mathrm{1} \\ $$$$=−.\mathrm{6}\boldsymbol{{i}}−\mathrm{35}.\mathrm{90}−\mathrm{1}.\mathrm{52}+\mathrm{180}=−\mathrm{2}.\mathrm{12}\boldsymbol{{i}}+\mathrm{144}.\mathrm{1} \\ $$$$=................ \\ $$$$\boldsymbol{{there}}\:\boldsymbol{{is}}\:\boldsymbol{{no}}\:\boldsymbol{{case}}\:\boldsymbol{{for}}:{A}+{B}+{C}=\mathrm{180}. \\ $$

Commented by prakash jain last updated on 14/Jun/17

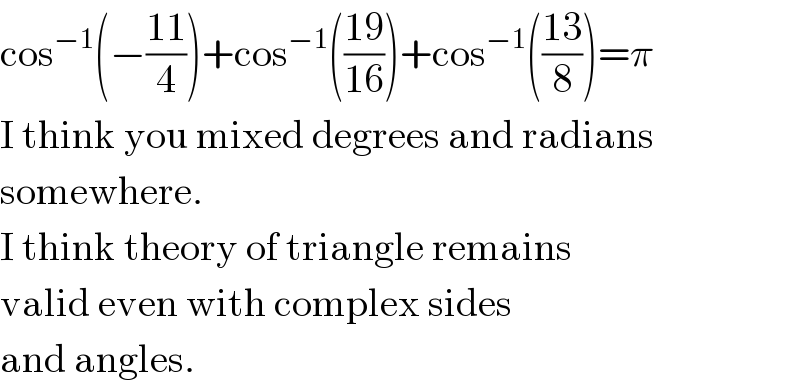
cos^(−1) (−((11)/4))+cos^(−1) (((19)/(16)))+cos^(−1) (((13)/8))=π I think you mixed degrees and radians somewhere. I think theory of triangle remains valid even with complex sides and angles.

$$\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{11}}{\mathrm{4}}\right)+\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{19}}{\mathrm{16}}\right)+\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{13}}{\mathrm{8}}\right)=\pi \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{mixed}\:\mathrm{degrees}\:\mathrm{and}\:\mathrm{radians} \\ $$$$\mathrm{somewhere}. \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{theory}\:\mathrm{of}\:\mathrm{triangle}\:\mathrm{remains} \\ $$$$\mathrm{valid}\:\mathrm{even}\:\mathrm{with}\:\mathrm{complex}\:\mathrm{sides} \\ $$$$\mathrm{and}\:\mathrm{angles}. \\ $$

Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 15/Jun/17

mr prakash! cos^(−1) (((19)/(16))),not a valid angle with primary elements of geometry and trigonometry.

$${mr}\:{prakash}!\:{cos}^{−\mathrm{1}} \left(\frac{\mathrm{19}}{\mathrm{16}}\right),{not}\:{a}\:{valid}\: \\ $$$${angle}\:{with}\:{primary}\:{elements}\:{of}\: \\ $$$${geometry}\:{and}\:{trigonometry}. \\ $$

Commented by prakash jain last updated on 18/Jun/17

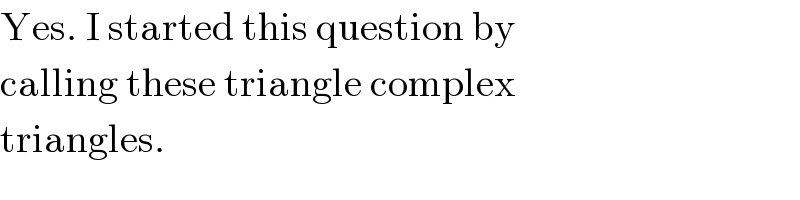
Yes. I started this question by calling these triangle complex triangles.

$$\mathrm{Yes}.\:\mathrm{I}\:\mathrm{started}\:\mathrm{this}\:\mathrm{question}\:\mathrm{by} \\ $$$$\mathrm{calling}\:\mathrm{these}\:\mathrm{triangle}\:\mathrm{complex} \\ $$$$\mathrm{triangles}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com