
Question and Answers Forum
Question Number 157665 by mnjuly1970 last updated on 26/Oct/21
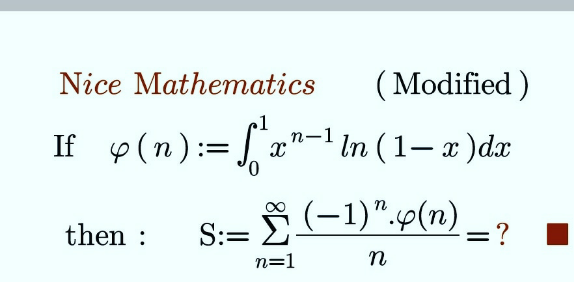
Answered by Raxreedoroid last updated on 26/Oct/21
![I=∫_0 ^( 1) x^(n−1) ln (1−x) dw=x^(n−1) ,w=(x^n /n) t=ln (1−x),dt=((−1)/(1−x))dx I=[((x^n ln (1−x))/n)+(1/n)∫(x^n /(1−x))dx]_0 ^1 u=1−x,x=1−u,dx=−du I=[(((1−u)^n ln (u))/n)−(1/n)∫(((1−u)^n )/u)du]_1 ^0 I=[(((1−u)^n ln (u))/n)+(1/n)∫(1−u)^(n−1) +(1/u)du]_1 ^0 I=[(((1−u)^n ln (u))/n)−(1/n)((((1−u)^n )/n)+ln u)]_1 ^0 I=[(((1−u)^n nln (u)−(1−u)^n −nln u)/n^2 )]_1 ^0 I=lim_(u→0^+ ) (((1−u)^n nln (u)−(1−u)^n −nln u)/n^2 ) I=lim_(u→0^+ ) ((nln u((1−u)^n −1)−(1−u)^n )/n^2 ) I=lim_(u→0^+ ) (((ln u((1−u)^n −1))/n))−(1/n^2 ) I=−(1/n^2 ) ϕ(n)=−(1/n^2 ) S=−Σ_(n=1) ^∞ (((−1)^n )/n^3 )=Σ_(n=1) ^∞ (1/n^3 )−2Σ_(n=1) ^∞ (1/((2n)^3 )) S=ζ(3)−2Σ_(n=1) ^∞ (1/(8n^3 ))=ζ(3)−(1/4)ζ(3) S=(3/4)ζ(3)](Q157684.png)
Answered by qaz last updated on 26/Oct/21
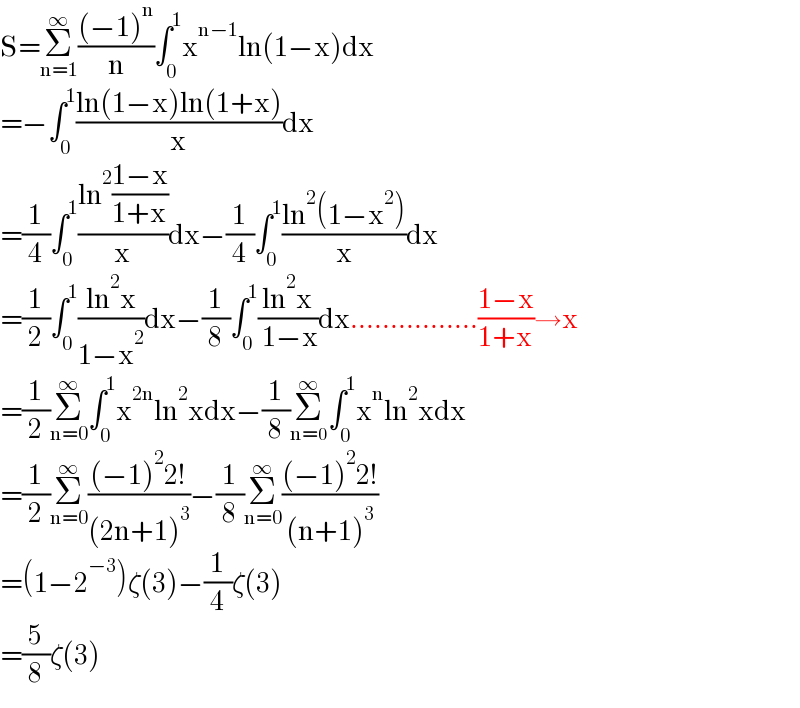
| ||
Question and Answers Forum | ||
Question Number 157665 by mnjuly1970 last updated on 26/Oct/21 | ||
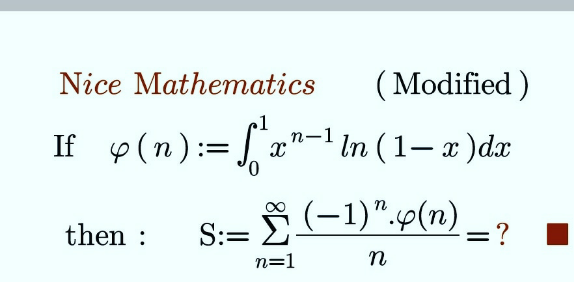 | ||
Answered by Raxreedoroid last updated on 26/Oct/21 | ||
![I=∫_0 ^( 1) x^(n−1) ln (1−x) dw=x^(n−1) ,w=(x^n /n) t=ln (1−x),dt=((−1)/(1−x))dx I=[((x^n ln (1−x))/n)+(1/n)∫(x^n /(1−x))dx]_0 ^1 u=1−x,x=1−u,dx=−du I=[(((1−u)^n ln (u))/n)−(1/n)∫(((1−u)^n )/u)du]_1 ^0 I=[(((1−u)^n ln (u))/n)+(1/n)∫(1−u)^(n−1) +(1/u)du]_1 ^0 I=[(((1−u)^n ln (u))/n)−(1/n)((((1−u)^n )/n)+ln u)]_1 ^0 I=[(((1−u)^n nln (u)−(1−u)^n −nln u)/n^2 )]_1 ^0 I=lim_(u→0^+ ) (((1−u)^n nln (u)−(1−u)^n −nln u)/n^2 ) I=lim_(u→0^+ ) ((nln u((1−u)^n −1)−(1−u)^n )/n^2 ) I=lim_(u→0^+ ) (((ln u((1−u)^n −1))/n))−(1/n^2 ) I=−(1/n^2 ) ϕ(n)=−(1/n^2 ) S=−Σ_(n=1) ^∞ (((−1)^n )/n^3 )=Σ_(n=1) ^∞ (1/n^3 )−2Σ_(n=1) ^∞ (1/((2n)^3 )) S=ζ(3)−2Σ_(n=1) ^∞ (1/(8n^3 ))=ζ(3)−(1/4)ζ(3) S=(3/4)ζ(3)](Q157684.png) | ||
| ||
Answered by qaz last updated on 26/Oct/21 | ||
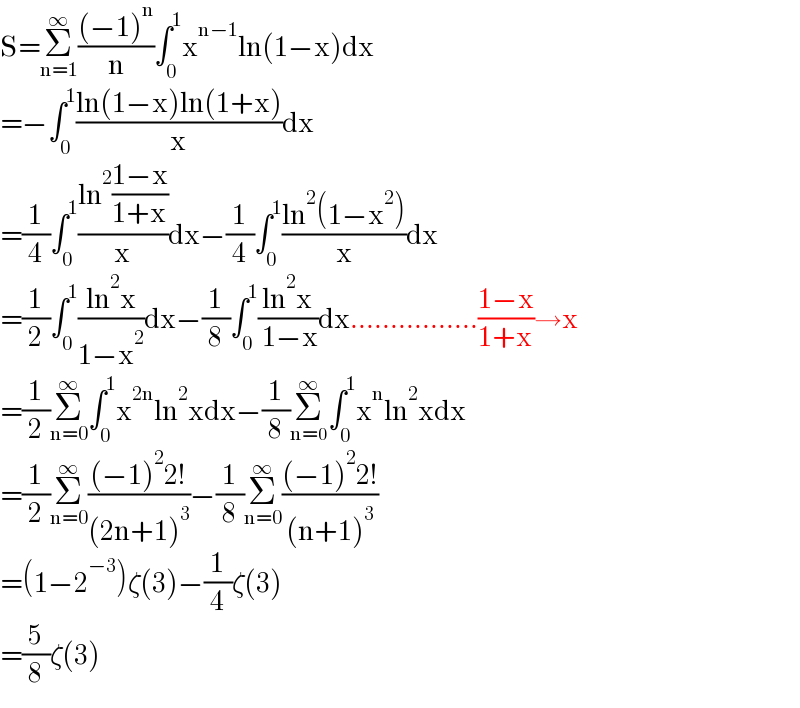 | ||
| ||