Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 15770 by arnabpapu550@gmail.com last updated on 13/Jun/17

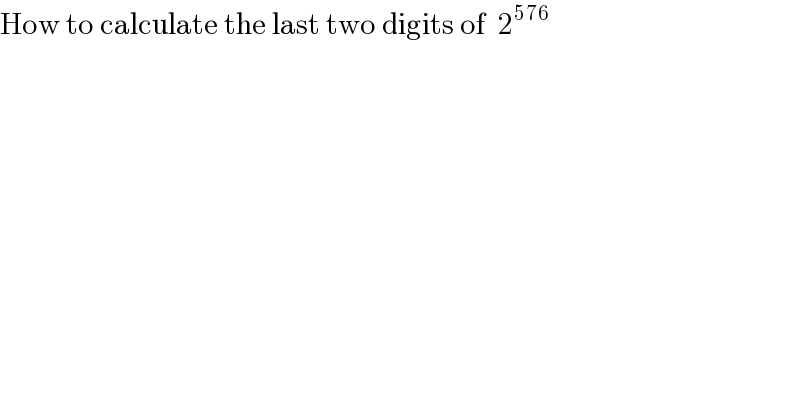
How to calculate the last two digits of 2^(576)

$$\mathrm{How}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{last}\:\mathrm{two}\:\mathrm{digits}\:\mathrm{of}\:\:\mathrm{2}^{\mathrm{576}} \\ $$

Answered by Tinkutara last updated on 14/Jun/17

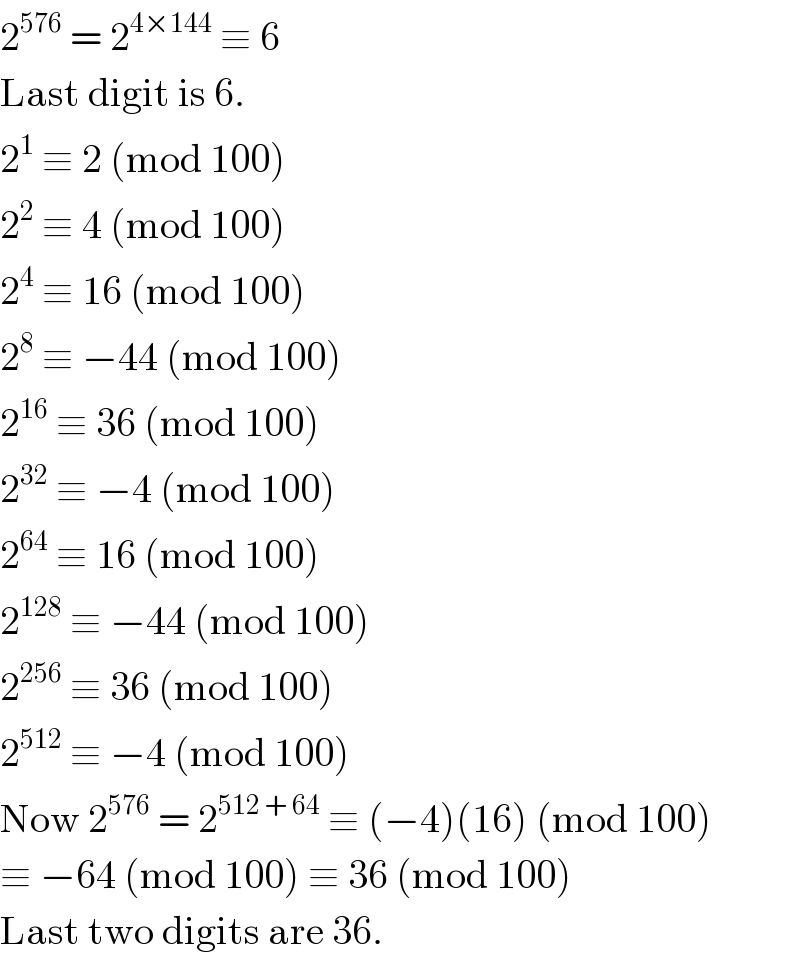
2^(576) = 2^(4×144) ≡ 6 Last digit is 6. 2^1 ≡ 2 (mod 100) 2^2 ≡ 4 (mod 100) 2^4 ≡ 16 (mod 100) 2^8 ≡ −44 (mod 100) 2^(16) ≡ 36 (mod 100) 2^(32) ≡ −4 (mod 100) 2^(64) ≡ 16 (mod 100) 2^(128) ≡ −44 (mod 100) 2^(256) ≡ 36 (mod 100) 2^(512) ≡ −4 (mod 100) Now 2^(576) = 2^(512 + 64) ≡ (−4)(16) (mod 100) ≡ −64 (mod 100) ≡ 36 (mod 100) Last two digits are 36.

$$\mathrm{2}^{\mathrm{576}} \:=\:\mathrm{2}^{\mathrm{4}×\mathrm{144}} \:\equiv\:\mathrm{6} \\ $$$$\mathrm{Last}\:\mathrm{digit}\:\mathrm{is}\:\mathrm{6}. \\ $$$$\mathrm{2}^{\mathrm{1}} \:\equiv\:\mathrm{2}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{2}} \:\equiv\:\mathrm{4}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{4}} \:\equiv\:\mathrm{16}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{8}} \:\equiv\:−\mathrm{44}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{16}} \:\equiv\:\mathrm{36}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{32}} \:\equiv\:−\mathrm{4}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{64}} \:\equiv\:\mathrm{16}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{128}} \:\equiv\:−\mathrm{44}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{256}} \:\equiv\:\mathrm{36}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{2}^{\mathrm{512}} \:\equiv\:−\mathrm{4}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{Now}\:\mathrm{2}^{\mathrm{576}} \:=\:\mathrm{2}^{\mathrm{512}\:+\:\mathrm{64}} \:\equiv\:\left(−\mathrm{4}\right)\left(\mathrm{16}\right)\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\equiv\:−\mathrm{64}\:\left(\mathrm{mod}\:\mathrm{100}\right)\:\equiv\:\mathrm{36}\:\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{Last}\:\mathrm{two}\:\mathrm{digits}\:\mathrm{are}\:\mathrm{36}. \\ $$

Commented by arnabpapu550@gmail.com last updated on 14/Jun/17

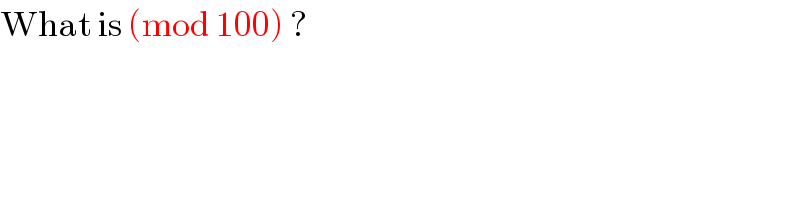
What is (mod 100) ?

$$\mathrm{What}\:\mathrm{is}\:\left(\mathrm{mod}\:\mathrm{100}\right)\:? \\ $$$$ \\ $$

Commented by arnabpapu550@gmail.com last updated on 14/Jun/17

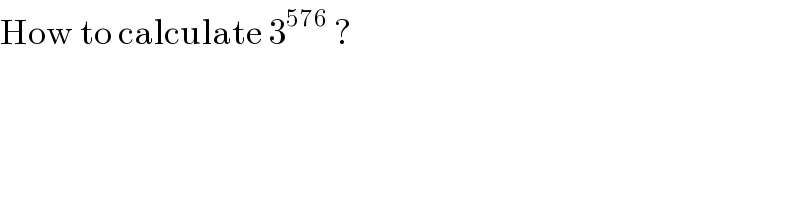
How to calculate 3^(576) ?

$$\mathrm{How}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{3}^{\mathrm{576}} \:? \\ $$

Commented by Tinkutara last updated on 14/Jun/17

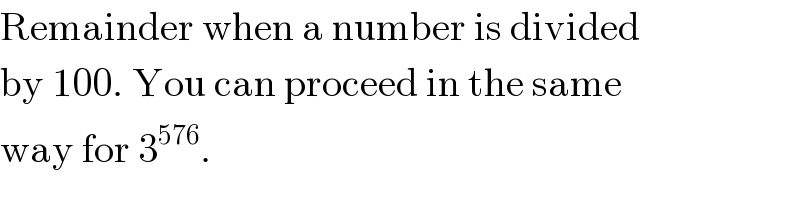
Remainder when a number is divided by 100. You can proceed in the same way for 3^(576) .

$$\mathrm{Remainder}\:\mathrm{when}\:\mathrm{a}\:\mathrm{number}\:\mathrm{is}\:\mathrm{divided} \\ $$$$\mathrm{by}\:\mathrm{100}.\:\mathrm{You}\:\mathrm{can}\:\mathrm{proceed}\:\mathrm{in}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{way}\:\mathrm{for}\:\mathrm{3}^{\mathrm{576}} . \\ $$

Commented by arnabpapu550@gmail.com last updated on 15/Jun/17

Now I am trying to calculate last two digits of 3^(576) 3^1 ≡3(mod 100) 3^2 ≡9(mod 100) 3^4 ≡−19(mod 100) 3^8 ≡−39(mod 100) 3^(16) ≡21(mod 100) 3^(32) ≡41(mod100) 3^(64) ≡−19(mod 100) 3^(128) ≡−39(mod 100) 3^(256) ≡21(mod 100) 3^(512) =41(mod 100) ∴ 3^(576) =3^(512+64) =41×(−19)(mod 100) =21 Is it right?

$$\mathrm{Now}\:\mathrm{I}\:\mathrm{am}\:\mathrm{trying}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{last}\:\mathrm{two}\:\mathrm{digits} \\ $$$$\mathrm{of}\:\:\mathrm{3}^{\mathrm{576}} \\ $$$$\mathrm{3}^{\mathrm{1}} \equiv\mathrm{3}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{3}^{\mathrm{2}} \equiv\mathrm{9}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{3}^{\mathrm{4}} \equiv−\mathrm{19}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{3}^{\mathrm{8}} \equiv−\mathrm{39}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{3}^{\mathrm{16}} \equiv\mathrm{21}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{3}^{\mathrm{32}} \equiv\mathrm{41}\left(\mathrm{mod100}\right) \\ $$$$\mathrm{3}^{\mathrm{64}} \equiv−\mathrm{19}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{3}^{\mathrm{128}} \equiv−\mathrm{39}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{3}^{\mathrm{256}} \equiv\mathrm{21}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\mathrm{3}^{\mathrm{512}} =\mathrm{41}\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$\therefore\:\mathrm{3}^{\mathrm{576}} =\mathrm{3}^{\mathrm{512}+\mathrm{64}} =\mathrm{41}×\left(−\mathrm{19}\right)\left(\mathrm{mod}\:\mathrm{100}\right) \\ $$$$=\mathrm{21} \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{right}? \\ $$

Commented by arnabpapu550@gmail.com last updated on 14/Jun/17

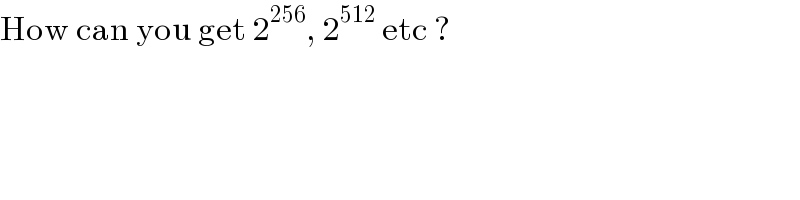
How can you get 2^(256) , 2^(512) etc ?

$$\mathrm{How}\:\mathrm{can}\:\mathrm{you}\:\mathrm{get}\:\mathrm{2}^{\mathrm{256}} ,\:\mathrm{2}^{\mathrm{512}} \:\mathrm{etc}\:? \\ $$

Commented by Tinkutara last updated on 15/Jun/17

Square the remainders obtained in previous step and find their remainders when divided by 100. For easy calculation and simplification, if the remainders are greater than 50, subtract 100 from them and put a minus sign. Now repeat the same procedure again and again.

$$\mathrm{Square}\:\mathrm{the}\:\mathrm{remainders}\:\mathrm{obtained}\:\mathrm{in} \\ $$$$\mathrm{previous}\:\mathrm{step}\:\mathrm{and}\:\mathrm{find}\:\mathrm{their}\:\mathrm{remainders} \\ $$$$\mathrm{when}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{100}.\:\mathrm{For}\:\mathrm{easy} \\ $$$$\mathrm{calculation}\:\mathrm{and}\:\mathrm{simplification},\:\mathrm{if}\:\mathrm{the} \\ $$$$\mathrm{remainders}\:\mathrm{are}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{50}, \\ $$$$\mathrm{subtract}\:\mathrm{100}\:\mathrm{from}\:\mathrm{them}\:\mathrm{and}\:\mathrm{put}\:\mathrm{a}\:\mathrm{minus} \\ $$$$\mathrm{sign}.\:\mathrm{Now}\:\mathrm{repeat}\:\mathrm{the}\:\mathrm{same}\:\mathrm{procedure} \\ $$$$\mathrm{again}\:\mathrm{and}\:\mathrm{again}. \\ $$

Commented by Tinkutara last updated on 15/Jun/17

Yes!

$$\mathrm{Yes}! \\ $$

Commented by arnabpapu550@gmail.com last updated on 15/Jun/17

Thank you very much.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com