
Question and Answers Forum
Question Number 1581 by 112358 last updated on 21/Aug/15
![Find a function f(x) satisfying the following equation. ∫_a ^( b) [(1/2){f(x)}^2 −(√({f(x)}^2 +{(d/dx)(f(x))}^2 ))]dx=0 b>0,a>0 , b≠a.](Q1581.png)
Commented by123456 last updated on 21/Aug/15
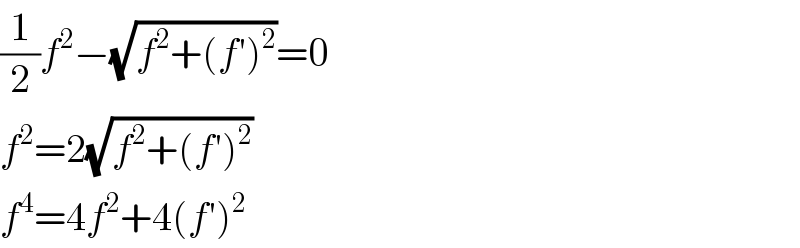
Commented by112358 last updated on 25/Aug/15
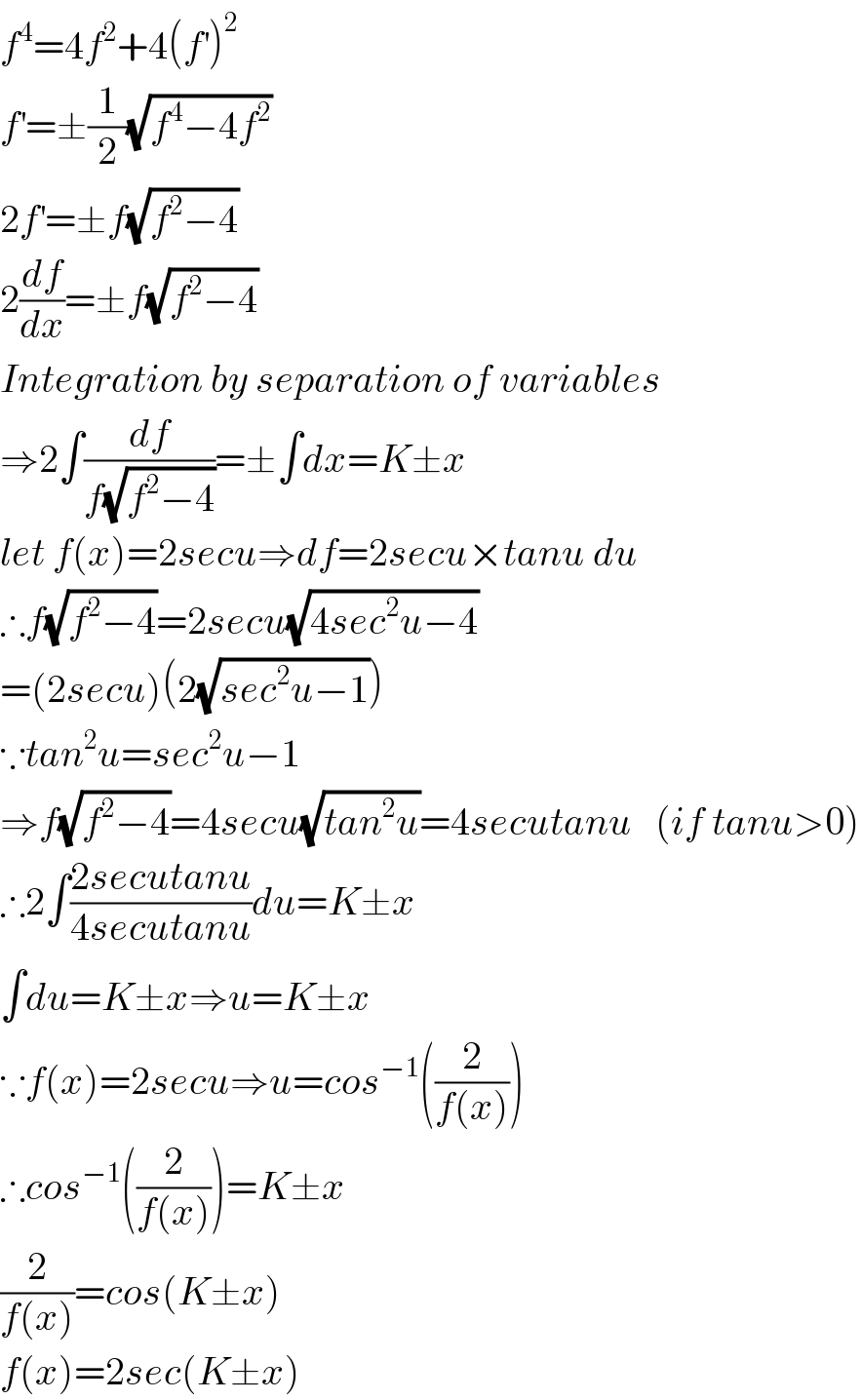
| ||
Question and Answers Forum | ||
Question Number 1581 by 112358 last updated on 21/Aug/15 | ||
![Find a function f(x) satisfying the following equation. ∫_a ^( b) [(1/2){f(x)}^2 −(√({f(x)}^2 +{(d/dx)(f(x))}^2 ))]dx=0 b>0,a>0 , b≠a.](Q1581.png) | ||
Commented by123456 last updated on 21/Aug/15 | ||
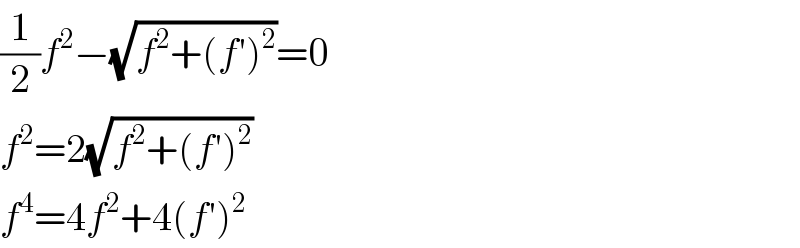 | ||
Commented by112358 last updated on 25/Aug/15 | ||
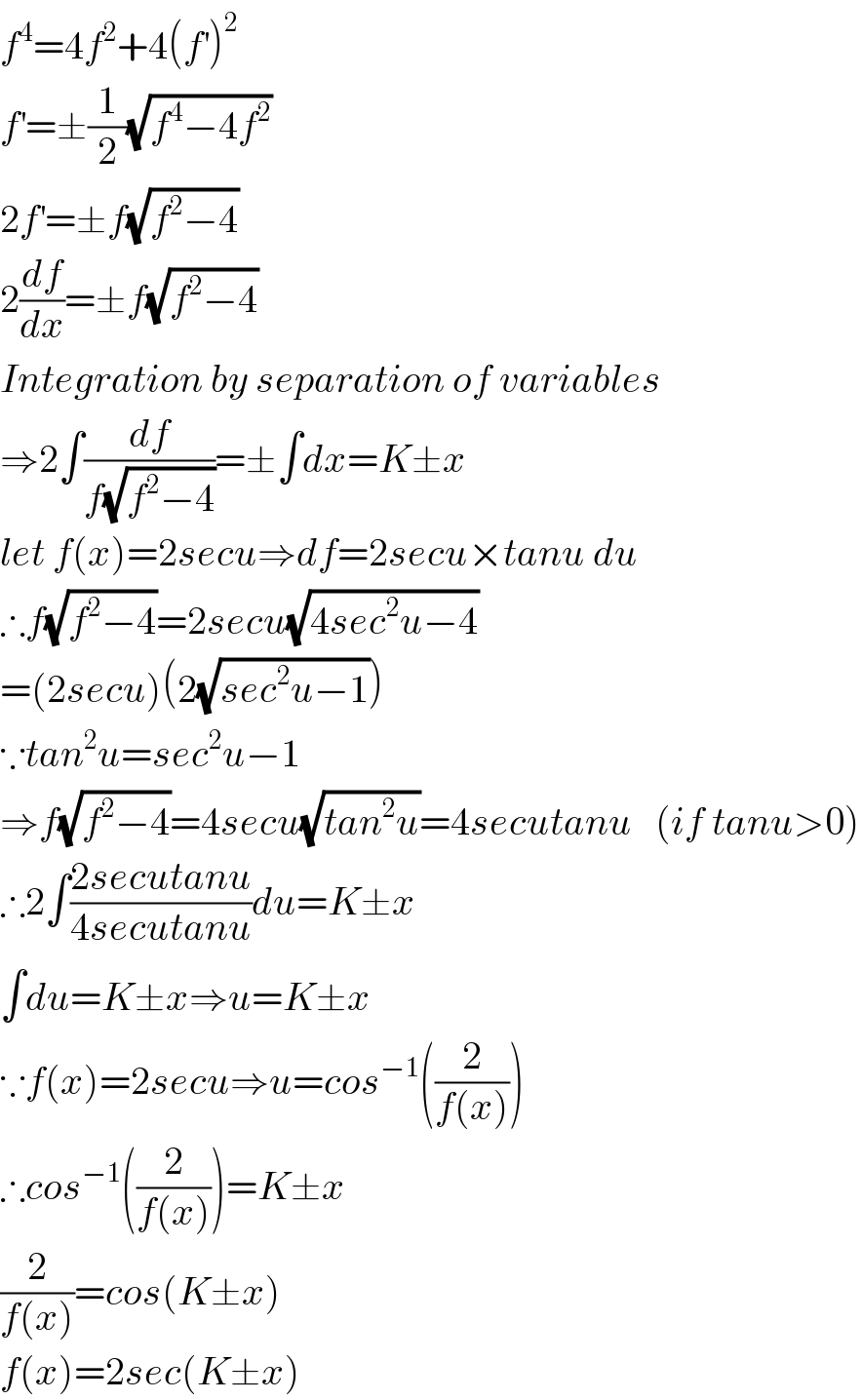 | ||