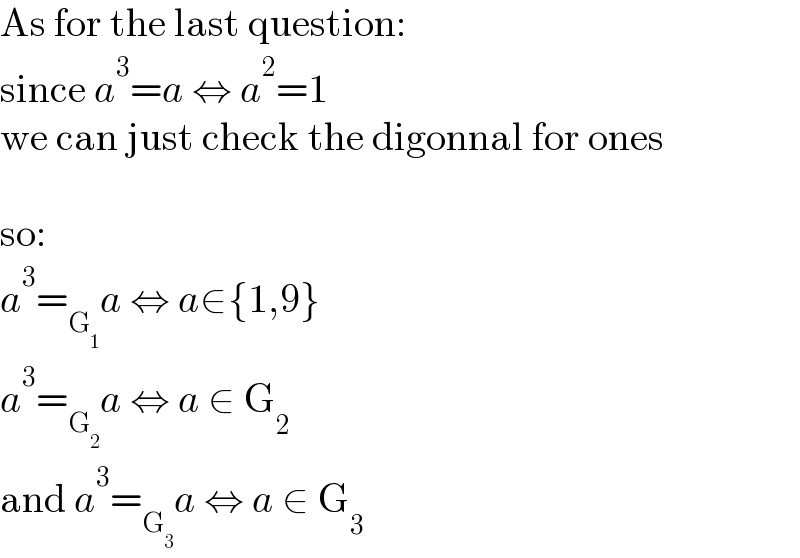Math Question and Answers


Question and Answers Forum

All Questions Topic List
Coordinate Geometry Questions
Previous in All Question Next in All Question
Previous in Coordinate Geometry Next in Coordinate Geometry
Question Number 158143 by alcohol last updated on 31/Oct/21

Commented by TheHoneyCat last updated on 31/Oct/21
$G_3 and G_2 are clearly isomorphical buy looking at their respectiv tables. we just need to map as follow: { (1,⇆,1),(5,⇆,3),(7,⇆,5),((11),⇆,7) :} G_1 cannot be isomorphic to either one because 3×_(10) 3=9≢1 [10] while ∀n∈{1,5,7,11} n×_(12) n=1 and ∀n∈{1,3,5,7} n×_8 n=1$
$G_{3} and G_{2} are clearly isomorphical buy looking$ $at their respectiv tables .$ $we just need to map as follow :$ ${\begin{cases} 1 & ⇆ & 1 \\ 5 & ⇆ & 3 \\ 7 & ⇆ & 5 \\ 11 & ⇆ & 7 \end{cases}$ $G_{1} cannot be isomorphic to either one because$ $3 \times_{10} 3 = 9 ≢ 1 [10]$ $while \forall n \in {1, 5, 7, 11} n \times_{12} n = 1$ $and \forall n \in {1, 3, 5, 7} n \times_{8} n = 1$
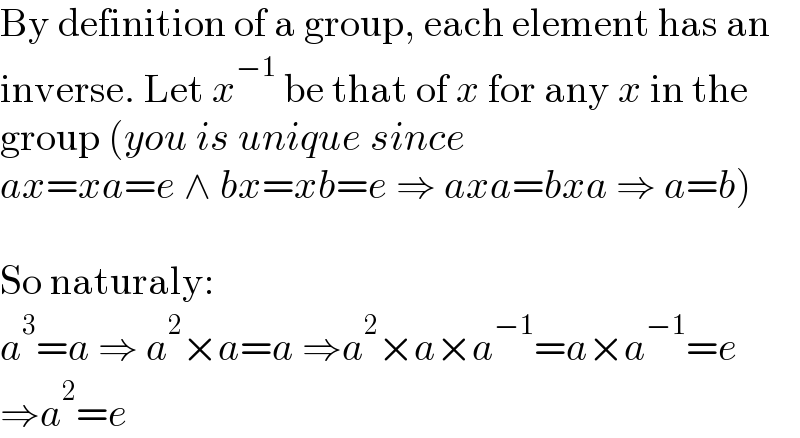
Commented by TheHoneyCat last updated on 31/Oct/21

$By definition of a group, each element has an$ $inverse . Let x^{- 1} be that of x for any x in the$ $group (y o u i s u n i q u e s i n c e$ $a x = x a = e \land b x = x b = e \Rightarrow a x a = b x a \Rightarrow a = b)$ $So naturaly :$ $a^{3} = a \Rightarrow a^{2} \times a = a \Rightarrow a^{2} \times a \times a^{- 1} = a \times a^{- 1} = e$ $\Rightarrow a^{2} = e$
Commented by TheHoneyCat last updated on 31/Oct/21

$G_{1} :$ $\| \begin{matrix} \times_{10} & 1 & 3 & 7 & 9 \\ 1 & 1 & 3 & 7 & 9 \\ 3 & 3 & 9 & 1 & 7 \\ 7 & 7 & 1 & 9 & 3 \\ 9 & 9 & 7 & 3 & 1 \end{matrix} \|$ $G_{2} :$ $\| \begin{matrix} \times_{12} & 1 & 5 & 7 & 11 \\ 1 & 1 & 5 & 7 & 11 \\ 5 & 5 & 1 & 11 & 7 \\ 7 & 7 & 11 & 1 & 5 \\ 11 & 11 & 7 & 5 & 1 \end{matrix} \|$ $G_{3} :$ $\| \begin{matrix} \times_{8} & 1 & 3 & 5 & 7 \\ 1 & 1 & 3 & 5 & 7 \\ 3 & 3 & 1 & 7 & 5 \\ 5 & 5 & 7 & 1 & 3 \\ 7 & 7 & 5 & 3 & 1 \end{matrix} \|$
Commented by TheHoneyCat last updated on 31/Oct/21
oups, I forgot to put the last one in blue...
Commented by phanphuoc last updated on 31/Oct/21

$y o u c a n p r o o f : g r o u p G s t \forall x \in G : x^{n} = e \to G a b e l$
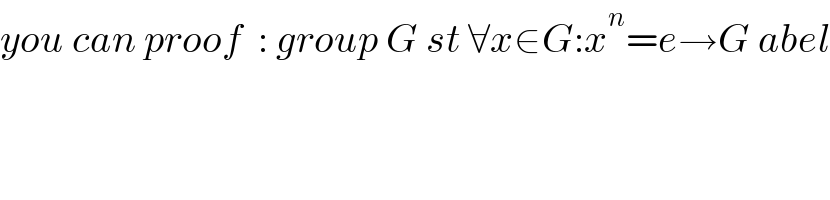
Commented by TheHoneyCat last updated on 31/Oct/21
it did say "∀x" but "∃a" so I just did not assume anything
	Answered by TheHoneyCat last updated on 31/Oct/21
	$As for the last question: since a^3 =a ⇔ a^2 =1 we can just check the digonnal for ones so: a^3 =_G_1 a ⇔ a∈{1,9} a^3 =_G_2 a ⇔ a ∈ G_2 and a^3 =_G_3 a ⇔ a ∈ G_3$
	$As for the last question :$ $since a^{3} = a \Leftrightarrow a^{2} = 1$ $we can just check the digonnal for ones$ $so :$ $a^{3} =_{G_{1}} a \Leftrightarrow a \in {1, 9}$ $a^{3} =_{G_{2}} a \Leftrightarrow a \in G_{2}$ $and a^{3} =_{G_{3}} a \Leftrightarrow a \in G_{3}$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum