Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 158469 by zakirullah last updated on 04/Nov/21

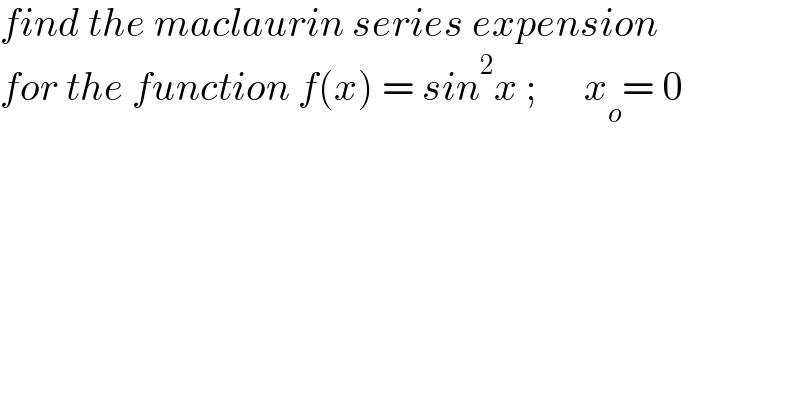
find the maclaurin series expension for the function f(x) = sin^2 x ; x_o = 0

$${find}\:{the}\:{maclaurin}\:{series}\:{expension} \\ $$$${for}\:{the}\:{function}\:{f}\left({x}\right)\:=\:{sin}^{\mathrm{2}} {x}\:;\:\:\:\:\:\:{x}_{{o}} =\:\mathrm{0} \\ $$

Answered by TheSupreme last updated on 04/Nov/21

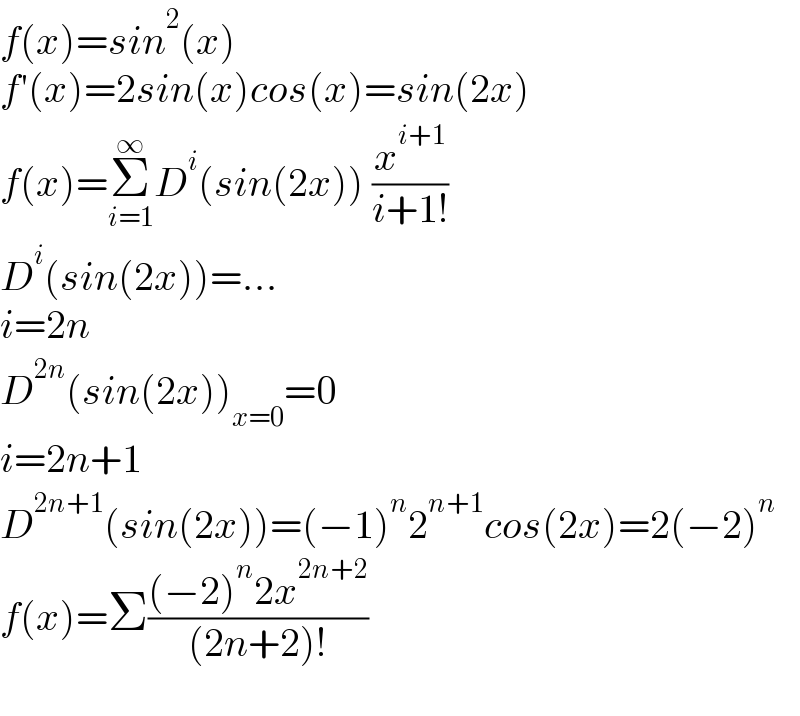
f(x)=sin^2 (x) f′(x)=2sin(x)cos(x)=sin(2x) f(x)=Σ_(i=1) ^∞ D^i (sin(2x)) (x^(i+1) /(i+1!)) D^i (sin(2x))=... i=2n D^(2n) (sin(2x))_(x=0) =0 i=2n+1 D^(2n+1) (sin(2x))=(−1)^n 2^(n+1) cos(2x)=2(−2)^n f(x)=Σ(((−2)^n 2x^(2n+2) )/((2n+2)!))

$${f}\left({x}\right)={sin}^{\mathrm{2}} \left({x}\right) \\ $$$${f}'\left({x}\right)=\mathrm{2}{sin}\left({x}\right){cos}\left({x}\right)={sin}\left(\mathrm{2}{x}\right) \\ $$$${f}\left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{D}^{{i}} \left({sin}\left(\mathrm{2}{x}\right)\right)\:\frac{{x}^{{i}+\mathrm{1}} }{{i}+\mathrm{1}!} \\ $$$${D}^{{i}} \left({sin}\left(\mathrm{2}{x}\right)\right)=... \\ $$$${i}=\mathrm{2}{n} \\ $$$${D}^{\mathrm{2}{n}} \left({sin}\left(\mathrm{2}{x}\right)\right)_{{x}=\mathrm{0}} =\mathrm{0} \\ $$$${i}=\mathrm{2}{n}+\mathrm{1} \\ $$$${D}^{\mathrm{2}{n}+\mathrm{1}} \left({sin}\left(\mathrm{2}{x}\right)\right)=\left(−\mathrm{1}\right)^{{n}} \mathrm{2}^{{n}+\mathrm{1}} {cos}\left(\mathrm{2}{x}\right)=\mathrm{2}\left(−\mathrm{2}\right)^{{n}} \\ $$$${f}\left({x}\right)=\Sigma\frac{\left(−\mathrm{2}\right)^{{n}} \mathrm{2}{x}^{\mathrm{2}{n}+\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{2}\right)!} \\ $$$$ \\ $$

Commented by zakirullah last updated on 04/Nov/21

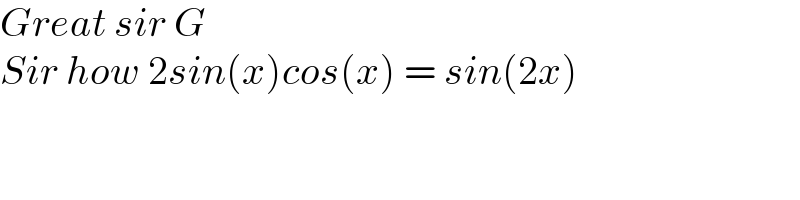
Great sir G Sir how 2sin(x)cos(x) = sin(2x)

$${Great}\:{sir}\:{G} \\ $$$${Sir}\:{how}\:\mathrm{2}{sin}\left({x}\right){cos}\left({x}\right)\:=\:{sin}\left(\mathrm{2}{x}\right) \\ $$

Commented by MJS_new last updated on 05/Nov/21

2sin x cos x =2×((e^(ix) −e^(−ix) )/(2i))×((e^(ix) +e^(−ix) )/2)= [(a−b)(a+b)=a^2 +b^2 ] =((e^(2ix) −e^(−2ix) )/(2i))=sin 2x

$$\mathrm{2sin}\:{x}\:\mathrm{cos}\:{x}\:=\mathrm{2}×\frac{\mathrm{e}^{\mathrm{i}{x}} −\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2i}}×\frac{\mathrm{e}^{\mathrm{i}{x}} +\mathrm{e}^{−\mathrm{i}{x}} }{\mathrm{2}}= \\ $$$$\:\:\:\:\:\left[\left({a}−{b}\right)\left({a}+{b}\right)={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right] \\ $$$$=\frac{\mathrm{e}^{\mathrm{2i}{x}} −\mathrm{e}^{−\mathrm{2i}{x}} }{\mathrm{2i}}=\mathrm{sin}\:\mathrm{2}{x} \\ $$

Commented by zakirullah last updated on 05/Nov/21

ok sir you′r the great

$${ok}\:{sir}\:{you}'{r}\:{the}\:{great} \\ $$

Commented by MJS_new last updated on 05/Nov/21

I′m just a tiny snip

$$\mathrm{I}'\mathrm{m}\:\mathrm{just}\:\mathrm{a}\:\mathrm{tiny}\:\mathrm{snip} \\ $$

Answered by mr W last updated on 04/Nov/21

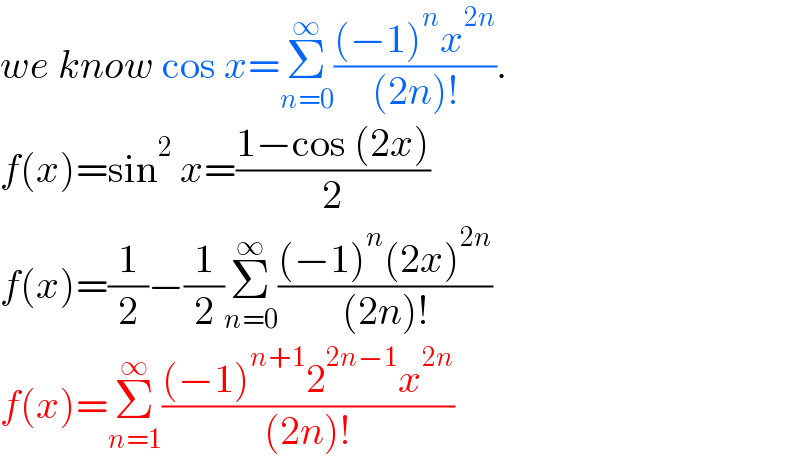
we know cos x=Σ_(n=0) ^∞ (((−1)^n x^(2n) )/((2n)!)). f(x)=sin^2 x=((1−cos (2x))/2) f(x)=(1/2)−(1/2)Σ_(n=0) ^∞ (((−1)^n (2x)^(2n) )/((2n)!)) f(x)=Σ_(n=1) ^∞ (((−1)^(n+1) 2^(2n−1) x^(2n) )/((2n)!))

$${we}\:{know}\:\mathrm{cos}\:{x}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}. \\ $$$${f}\left({x}\right)=\mathrm{sin}^{\mathrm{2}} \:{x}=\frac{\mathrm{1}−\mathrm{cos}\:\left(\mathrm{2}{x}\right)}{\mathrm{2}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{2}{x}\right)^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$$${f}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} {x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com