
Question and Answers Forum
Question Number 158477 by LEKOUMA last updated on 04/Nov/21
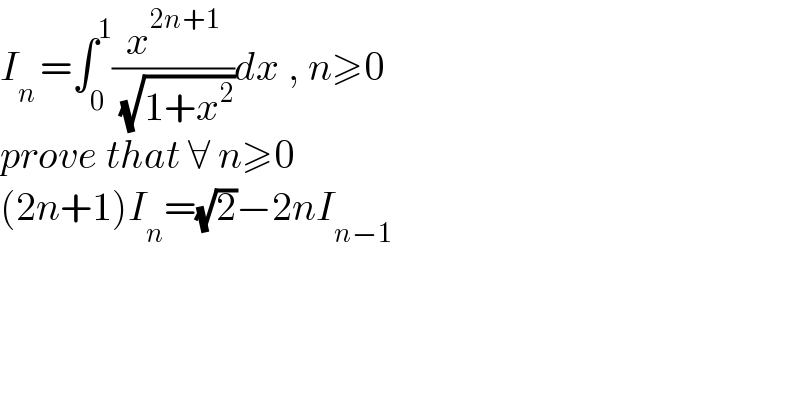
Answered by Ar Brandon last updated on 04/Nov/21
![I_n =∫_0 ^1 (x^(2n+1) /( (√(1+x^2 ))))dx, x=tanϑ⇒dx=sec^2 ϑdϑ =∫_0 ^(π/4) ((tan^(2n+1) ϑ)/(secϑ))∙sec^2 ϑdϑ=∫_0 ^(π/4) tan^(2n+1) ϑsecϑdϑ =∫_0 ^(π/4) tan^(2n) ϑ∙secϑtanϑdϑ, { ((u(ϑ)=tan^(2n) ϑ)),((v′(ϑ)=secϑtanϑ)) :} ⇒ { ((u′(ϑ)=2ntan^(2n−1) ϑsec^2 ϑ)),((v(ϑ)=secϑ)) :} =[tan^(2n) ϑsecϑ]_0 ^(π/4) −2n∫_0 ^(π/4) tan^(2n−1) sec^3 ϑdϑ =(√2)−2n∫_0 ^(π/4) tan^(2n−1) secϑdϑ−2n∫_0 ^(π/4) tan^(2n+1) ϑsecϑdϑ =(√2)−2nI_(n−1) −2nI_n ⇒ determinant ((((2n+1)I_n =(√2)−2nI_(n−1) )))](Q158490.png)
Answered by Ar Brandon last updated on 04/Nov/21
![I_n =∫_0 ^1 (x^(2n+1) /( (√(1+x^2 ))))dx=(1/2)∫_0 ^1 x^(2n) ∙((2x)/( (√(1+x^2 ))))dx { ((u(x)=x^(2n) )),((v′(x)=((2x)/( (√(1+x^2 )))))) :}⇒ { ((u′(x)=2nx^(2n−1) )),((v(x)=2(√(1+x^2 )))) :} I_n =[x^(2n) (√(1+x^2 ))]_0 ^1 −2n∫_0 ^1 x^(2n−1) (√(1+x^2 ))dx =(√2)−2n∫_0 ^1 ((x^(2n−1) (1+x^2 ))/( (√(1+x^2 ))))dx =(√2)−2n∫_0 ^1 (x^(2n−1) /( (√(1+x^2 ))))dx−2n∫_0 ^1 (x^(2n+1) /( (√(1+x^2 ))))dx =(√2)−2nI_(n−1) −2nI_n ⇒ determinant ((((2n+1)I_n =(√2)−2nI_(n−1) )))](Q158491.png)
Commented by mnjuly1970 last updated on 05/Nov/21

| ||
Question and Answers Forum | ||
Question Number 158477 by LEKOUMA last updated on 04/Nov/21 | ||
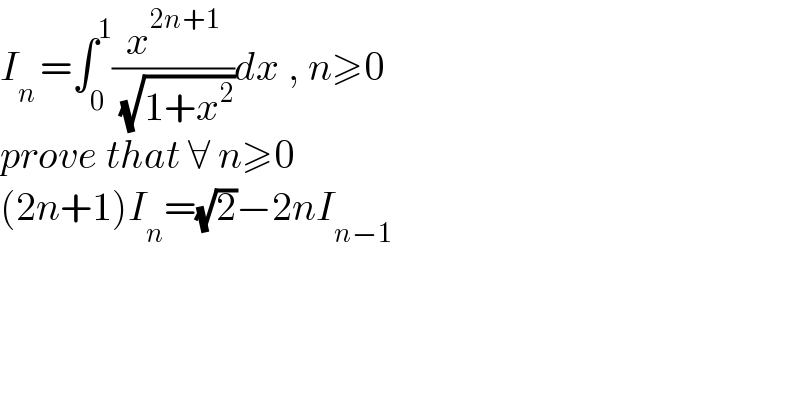 | ||
Answered by Ar Brandon last updated on 04/Nov/21 | ||
![I_n =∫_0 ^1 (x^(2n+1) /( (√(1+x^2 ))))dx, x=tanϑ⇒dx=sec^2 ϑdϑ =∫_0 ^(π/4) ((tan^(2n+1) ϑ)/(secϑ))∙sec^2 ϑdϑ=∫_0 ^(π/4) tan^(2n+1) ϑsecϑdϑ =∫_0 ^(π/4) tan^(2n) ϑ∙secϑtanϑdϑ, { ((u(ϑ)=tan^(2n) ϑ)),((v′(ϑ)=secϑtanϑ)) :} ⇒ { ((u′(ϑ)=2ntan^(2n−1) ϑsec^2 ϑ)),((v(ϑ)=secϑ)) :} =[tan^(2n) ϑsecϑ]_0 ^(π/4) −2n∫_0 ^(π/4) tan^(2n−1) sec^3 ϑdϑ =(√2)−2n∫_0 ^(π/4) tan^(2n−1) secϑdϑ−2n∫_0 ^(π/4) tan^(2n+1) ϑsecϑdϑ =(√2)−2nI_(n−1) −2nI_n ⇒ determinant ((((2n+1)I_n =(√2)−2nI_(n−1) )))](Q158490.png) | ||
| ||
Answered by Ar Brandon last updated on 04/Nov/21 | ||
![I_n =∫_0 ^1 (x^(2n+1) /( (√(1+x^2 ))))dx=(1/2)∫_0 ^1 x^(2n) ∙((2x)/( (√(1+x^2 ))))dx { ((u(x)=x^(2n) )),((v′(x)=((2x)/( (√(1+x^2 )))))) :}⇒ { ((u′(x)=2nx^(2n−1) )),((v(x)=2(√(1+x^2 )))) :} I_n =[x^(2n) (√(1+x^2 ))]_0 ^1 −2n∫_0 ^1 x^(2n−1) (√(1+x^2 ))dx =(√2)−2n∫_0 ^1 ((x^(2n−1) (1+x^2 ))/( (√(1+x^2 ))))dx =(√2)−2n∫_0 ^1 (x^(2n−1) /( (√(1+x^2 ))))dx−2n∫_0 ^1 (x^(2n+1) /( (√(1+x^2 ))))dx =(√2)−2nI_(n−1) −2nI_n ⇒ determinant ((((2n+1)I_n =(√2)−2nI_(n−1) )))](Q158491.png) | ||
| ||
Commented by mnjuly1970 last updated on 05/Nov/21 | ||
 | ||