
Question Number 1585 by Rasheed Soomro last updated on 22/Aug/15

$$\mathrm{Let}\:\omega\:\mathrm{is}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}\:\mathrm{and}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\in\:\mathbb{Z} \\ $$$$\mathrm{If}\:\omega^{\mathrm{x}} +\omega^{\mathrm{y}} +\omega^{\mathrm{z}} =\mathrm{0}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{3}\:\mid\:\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right) \\ $$$$\mathrm{Show}\:{by}\:{an}\:{example}\:\mathrm{that}\:\mathrm{the}\:\mathrm{converse}\:\mathrm{is}\:{not}\:\:\mathrm{true}. \\ $$
Commented by 112358 last updated on 22/Aug/15
![ω^3 −1=0 Cube root of unity⇒ω=e^((2kπi)/3) ,k=−1,0,1 Let ψ(x,y,z)=ω^x +ω^y +ω^z =e^((2xπik)/3) +e^((2kπiy)/3) +e^((2kπiz)/3) ψ(x,y,z)=cos(((2πxk)/3))+cos(((2πyk)/3))+cos(((2πzk)/3))+i[sin(((2kxπ)/3))+sin(((2πyk)/3))+sin(((2πzk)/3))] If ψ(x,y,z)=0⇒Re(ψ(x,y,z))=0 ,Im(ψ(x,y,z))=0 ∴cos(((2πxk)/3))+cos(((2πyk)/3))+cos(((2πzk)/3))=0 and sin(((2πxk)/3))+sin(((2πyk)/3))+sin(((2πzk)/3))=0 for k=−1,0,1 and x,y,z∈Z](Q1586.png)
$$\omega^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$${Cube}\:{root}\:{of}\:{unity}\Rightarrow\omega={e}^{\frac{\mathrm{2}{k}\pi{i}}{\mathrm{3}}} \:,{k}=−\mathrm{1},\mathrm{0},\mathrm{1} \\ $$$${Let} \\ $$$$\psi\left({x},{y},{z}\right)=\omega^{{x}} +\omega^{{y}} +\omega^{{z}} ={e}^{\frac{\mathrm{2}{x}\pi{ik}}{\mathrm{3}}} +{e}^{\frac{\mathrm{2}{k}\pi{iy}}{\mathrm{3}}} +{e}^{\frac{\mathrm{2}{k}\pi{iz}}{\mathrm{3}}} \\ $$$$\psi\left({x},{y},{z}\right)={cos}\left(\frac{\mathrm{2}\pi{xk}}{\mathrm{3}}\right)+{cos}\left(\frac{\mathrm{2}\pi{yk}}{\mathrm{3}}\right)+{cos}\left(\frac{\mathrm{2}\pi{zk}}{\mathrm{3}}\right)+{i}\left[{sin}\left(\frac{\mathrm{2}{kx}\pi}{\mathrm{3}}\right)+{sin}\left(\frac{\mathrm{2}\pi{yk}}{\mathrm{3}}\right)+{sin}\left(\frac{\mathrm{2}\pi{zk}}{\mathrm{3}}\right)\right] \\ $$$${If}\:\psi\left({x},{y},{z}\right)=\mathrm{0}\Rightarrow{Re}\left(\psi\left({x},{y},{z}\right)\right)=\mathrm{0}\:,{Im}\left(\psi\left({x},{y},{z}\right)\right)=\mathrm{0} \\ $$$$\therefore{cos}\left(\frac{\mathrm{2}\pi{xk}}{\mathrm{3}}\right)+{cos}\left(\frac{\mathrm{2}\pi{yk}}{\mathrm{3}}\right)+{cos}\left(\frac{\mathrm{2}\pi{zk}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$${and}\: \\ $$$${sin}\left(\frac{\mathrm{2}\pi{xk}}{\mathrm{3}}\right)+{sin}\left(\frac{\mathrm{2}\pi{yk}}{\mathrm{3}}\right)+{sin}\left(\frac{\mathrm{2}\pi{zk}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$${for}\:{k}=−\mathrm{1},\mathrm{0},\mathrm{1}\:{and}\:{x},{y},{z}\in\mathbb{Z} \\ $$$$ \\ $$$$ \\ $$
Commented by 123456 last updated on 22/Aug/15
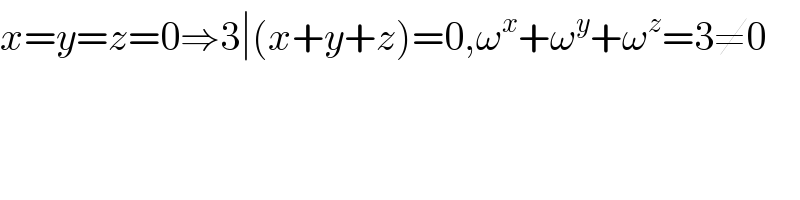
$${x}={y}={z}=\mathrm{0}\Rightarrow\mathrm{3}\mid\left({x}+{y}+{z}\right)=\mathrm{0},\omega^{{x}} +\omega^{{y}} +\omega^{{z}} =\mathrm{3}\neq\mathrm{0} \\ $$
Answered by 123456 last updated on 23/Aug/15
![ω=e^(((2π)/3)ι) =cos ((2π)/3)+ısin ((2π)/3) some fact that help theorem: if z_1 ,z_2 ,z_3 are 3 unitary complex number such that their sum is 0, then the angle betwen them is 120° proof: since z_1 ,z_2 ,z_3 are unitary, we can write ∣z_1 ∣=∣z_2 ∣=∣z_3 ∣=1 z_1 =e^(φı) =cos φ+ısin φ z_2 =e^((φ+θ_1 )ı) =cos(φ+θ_1 )+ısin(φ+θ_1 ) z_3 =e^((φ+θ_2 )ı) =cos(φ+θ_2 )+ısin(φ+θ_2 ) z_1 +z_2 +z_3 =0 e^(φı) +e^((φ+θ_1 )ı) +e^((φ+θ_2 )ı) =0 cos φ+ısin φ+cos(φ+θ_1 )+ısin(φ+θ_1 )+cos(φ+θ_2 )+ısin(φ+θ_2 )=0 [cos φ+cos(φ+θ_1 )+cos(φ+θ_2 )]+ı[sin φ+sin(φ+θ_1 )+sin(φ+θ_2 )]=0 { ((cos φ+cos(φ+θ_1 )+cos(φ+θ_2 )=0)),((sin φ+sin(φ+θ_1 )+sin(φ+θ_2 )=0)) :} cos(α+β)=cos α cos β−sin α sin β sin(α+β)=cos α sin β+cos β sin α { ((cos φ(1+cos θ_1 +cos θ_2 )−sin φ(sin θ_1 +sin θ_2 )=0)),((sin φ(1+cos θ_1 +cos θ_2 )+cos φ(sin θ_1 +sin θ_2 )=0)) :} cos φ=a,sin φ=b,1+cos θ_1 +cos θ_2 =x,sin θ_1 +sin θ_2 =y,a^2 +b^2 =1 { ((ax−by=0)),((bx+ay=0)) :} Δ= determinant ((a,(−b)),(b,a))=a^2 +b^2 =1 Δx= determinant ((0,(−b)),(0,a))=0 Δy= determinant ((a,0),(b,0))=0 x=((Δx)/Δ)=0 y=((Δy)/Δ)=0 { ((1+cos θ_1 +cos θ_2 =0)),((sin θ_1 +sin θ_2 =0)) :} sin θ_1 =sin −θ_2 ⇔θ_1 =−θ_2 +2πk∨θ_1 =π+θ_2 +2πk,k∈Z θ_1 =π+θ_2 +2πk⇒1+cos θ_1 +cos θ_2 =1+cos(π+θ_2 +2πk)+cos θ_2 =1−cos θ_2 +cos θ_2 =1≠0 θ_1 =−θ_2 +2πk⇒1+cos θ_1 +cos θ_2 =1+cos(−θ_2 +2πk)+cos θ_2 =1+cos θ_2 +cos θ_2 =1+2cos θ_2 =0 cos θ_2 =−(1/2) θ_2 =((2π)/3)+2πj∨θ_2 =((4π)/3)+2πj,j∈Z θ_1 =−((2π)/3)+2π(j+k)∨θ_2 =−((4π)/3)+2π(j+k). the cube roots of unity are 1,e^(((2π)/3)ı) ,e^(((4π)/3)j) ⇒1,ω,ω^2 ω^n =1,n≡0(mod 3) ω^n =e^(((2π)/3)ı) ,n≡1(mod 3) ω^n =e^(((4π)/3)ı) ,n≡2(mod 3) then for ω^x +ω^y +ω^z =0 as shown above, them need to have a angle of 120° betwen them, wich imply that all the three roots apear, without loss of generaly take x≡0(mod 3) y≡1(mod 3) z≡2(mod 3) them x+y+z≡0+1+2≡3≡0(mod 3) wich imply that 3∣(x+y+z)](Q1588.png)
$$\omega={e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}\iota} =\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}}+\imath\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{some}\:\mathrm{fact}\:\mathrm{that}\:\mathrm{help} \\ $$$$\boldsymbol{\mathrm{theorem}}: \\ $$$$\mathrm{if}\:{z}_{\mathrm{1}} ,{z}_{\mathrm{2}} ,{z}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{3}\:\mathrm{unitary}\:\mathrm{complex}\:\mathrm{number} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{their}\:\mathrm{sum}\:\mathrm{is}\:\mathrm{0},\:\mathrm{then}\:\mathrm{the}\:\mathrm{angle} \\ $$$$\mathrm{betwen}\:\mathrm{them}\:\mathrm{is}\:\mathrm{120}° \\ $$$$\boldsymbol{\mathrm{proof}}: \\ $$$$\mathrm{since}\:{z}_{\mathrm{1}} ,{z}_{\mathrm{2}} ,{z}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{unitary},\:\mathrm{we}\:\mathrm{can}\:\mathrm{write} \\ $$$$\mid{z}_{\mathrm{1}} \mid=\mid{z}_{\mathrm{2}} \mid=\mid{z}_{\mathrm{3}} \mid=\mathrm{1} \\ $$$${z}_{\mathrm{1}} ={e}^{\phi\imath} =\mathrm{cos}\:\phi+\imath\mathrm{sin}\:\phi \\ $$$${z}_{\mathrm{2}} ={e}^{\left(\phi+\theta_{\mathrm{1}} \right)\imath} =\mathrm{cos}\left(\phi+\theta_{\mathrm{1}} \right)+\imath\mathrm{sin}\left(\phi+\theta_{\mathrm{1}} \right) \\ $$$${z}_{\mathrm{3}} ={e}^{\left(\phi+\theta_{\mathrm{2}} \right)\imath} =\mathrm{cos}\left(\phi+\theta_{\mathrm{2}} \right)+\imath\mathrm{sin}\left(\phi+\theta_{\mathrm{2}} \right) \\ $$$${z}_{\mathrm{1}} +{z}_{\mathrm{2}} +{z}_{\mathrm{3}} =\mathrm{0} \\ $$$${e}^{\phi\imath} +{e}^{\left(\phi+\theta_{\mathrm{1}} \right)\imath} +{e}^{\left(\phi+\theta_{\mathrm{2}} \right)\imath} =\mathrm{0} \\ $$$$\mathrm{cos}\:\phi+\imath\mathrm{sin}\:\phi+\mathrm{cos}\left(\phi+\theta_{\mathrm{1}} \right)+\imath\mathrm{sin}\left(\phi+\theta_{\mathrm{1}} \right)+\mathrm{cos}\left(\phi+\theta_{\mathrm{2}} \right)+\imath\mathrm{sin}\left(\phi+\theta_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left[\mathrm{cos}\:\phi+\mathrm{cos}\left(\phi+\theta_{\mathrm{1}} \right)+\mathrm{cos}\left(\phi+\theta_{\mathrm{2}} \right)\right]+\imath\left[\mathrm{sin}\:\phi+\mathrm{sin}\left(\phi+\theta_{\mathrm{1}} \right)+\mathrm{sin}\left(\phi+\theta_{\mathrm{2}} \right)\right]=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{cos}\:\phi+\mathrm{cos}\left(\phi+\theta_{\mathrm{1}} \right)+\mathrm{cos}\left(\phi+\theta_{\mathrm{2}} \right)=\mathrm{0}}\\{\mathrm{sin}\:\phi+\mathrm{sin}\left(\phi+\theta_{\mathrm{1}} \right)+\mathrm{sin}\left(\phi+\theta_{\mathrm{2}} \right)=\mathrm{0}}\end{cases} \\ $$$$\mathrm{cos}\left(\alpha+\beta\right)=\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta \\ $$$$\mathrm{sin}\left(\alpha+\beta\right)=\mathrm{cos}\:\alpha\:\mathrm{sin}\:\beta+\mathrm{cos}\:\beta\:\mathrm{sin}\:\alpha \\ $$$$\begin{cases}{\mathrm{cos}\:\phi\left(\mathrm{1}+\mathrm{cos}\:\theta_{\mathrm{1}} +\mathrm{cos}\:\theta_{\mathrm{2}} \right)−\mathrm{sin}\:\phi\left(\mathrm{sin}\:\theta_{\mathrm{1}} +\mathrm{sin}\:\theta_{\mathrm{2}} \right)=\mathrm{0}}\\{\mathrm{sin}\:\phi\left(\mathrm{1}+\mathrm{cos}\:\theta_{\mathrm{1}} +\mathrm{cos}\:\theta_{\mathrm{2}} \right)+\mathrm{cos}\:\phi\left(\mathrm{sin}\:\theta_{\mathrm{1}} +\mathrm{sin}\:\theta_{\mathrm{2}} \right)=\mathrm{0}}\end{cases} \\ $$$$\mathrm{cos}\:\phi={a},\mathrm{sin}\:\phi={b},\mathrm{1}+\mathrm{cos}\:\theta_{\mathrm{1}} +\mathrm{cos}\:\theta_{\mathrm{2}} ={x},\mathrm{sin}\:\theta_{\mathrm{1}} +\mathrm{sin}\:\theta_{\mathrm{2}} ={y},{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\begin{cases}{{ax}−{by}=\mathrm{0}}\\{{bx}+{ay}=\mathrm{0}}\end{cases} \\ $$$$\Delta=\begin{vmatrix}{{a}}&{−{b}}\\{{b}}&{{a}}\end{vmatrix}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Delta{x}=\begin{vmatrix}{\mathrm{0}}&{−{b}}\\{\mathrm{0}}&{{a}}\end{vmatrix}=\mathrm{0} \\ $$$$\Delta{y}=\begin{vmatrix}{{a}}&{\mathrm{0}}\\{{b}}&{\mathrm{0}}\end{vmatrix}=\mathrm{0} \\ $$$${x}=\frac{\Delta{x}}{\Delta}=\mathrm{0} \\ $$$${y}=\frac{\Delta{y}}{\Delta}=\mathrm{0} \\ $$$$\begin{cases}{\mathrm{1}+\mathrm{cos}\:\theta_{\mathrm{1}} +\mathrm{cos}\:\theta_{\mathrm{2}} =\mathrm{0}}\\{\mathrm{sin}\:\theta_{\mathrm{1}} +\mathrm{sin}\:\theta_{\mathrm{2}} =\mathrm{0}}\end{cases} \\ $$$$\mathrm{sin}\:\theta_{\mathrm{1}} =\mathrm{sin}\:−\theta_{\mathrm{2}} \Leftrightarrow\theta_{\mathrm{1}} =−\theta_{\mathrm{2}} +\mathrm{2}\pi{k}\vee\theta_{\mathrm{1}} =\pi+\theta_{\mathrm{2}} +\mathrm{2}\pi{k},{k}\in\mathbb{Z} \\ $$$$\theta_{\mathrm{1}} =\pi+\theta_{\mathrm{2}} +\mathrm{2}\pi{k}\Rightarrow\mathrm{1}+\mathrm{cos}\:\theta_{\mathrm{1}} +\mathrm{cos}\:\theta_{\mathrm{2}} =\mathrm{1}+\mathrm{cos}\left(\pi+\theta_{\mathrm{2}} +\mathrm{2}\pi{k}\right)+\mathrm{cos}\:\theta_{\mathrm{2}} =\mathrm{1}−\mathrm{cos}\:\theta_{\mathrm{2}} +\mathrm{cos}\:\theta_{\mathrm{2}} =\mathrm{1}\neq\mathrm{0} \\ $$$$\theta_{\mathrm{1}} =−\theta_{\mathrm{2}} +\mathrm{2}\pi{k}\Rightarrow\mathrm{1}+\mathrm{cos}\:\theta_{\mathrm{1}} +\mathrm{cos}\:\theta_{\mathrm{2}} =\mathrm{1}+\mathrm{cos}\left(−\theta_{\mathrm{2}} +\mathrm{2}\pi{k}\right)+\mathrm{cos}\:\theta_{\mathrm{2}} =\mathrm{1}+\mathrm{cos}\:\theta_{\mathrm{2}} +\mathrm{cos}\:\theta_{\mathrm{2}} =\mathrm{1}+\mathrm{2cos}\:\theta_{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{cos}\:\theta_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\theta_{\mathrm{2}} =\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}\pi{j}\vee\theta_{\mathrm{2}} =\frac{\mathrm{4}\pi}{\mathrm{3}}+\mathrm{2}\pi{j},{j}\in\mathbb{Z} \\ $$$$\theta_{\mathrm{1}} =−\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}\pi\left({j}+{k}\right)\vee\theta_{\mathrm{2}} =−\frac{\mathrm{4}\pi}{\mathrm{3}}+\mathrm{2}\pi\left({j}+{k}\right). \\ $$$$\mathrm{the}\:\mathrm{cube}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity}\:\mathrm{are} \\ $$$$\mathrm{1},{e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}\imath} ,{e}^{\frac{\mathrm{4}\pi}{\mathrm{3}}{j}} \Rightarrow\mathrm{1},\omega,\omega^{\mathrm{2}} \\ $$$$\omega^{{n}} =\mathrm{1},{n}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\omega^{{n}} ={e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}\imath} ,{n}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\omega^{{n}} ={e}^{\frac{\mathrm{4}\pi}{\mathrm{3}}\imath} ,{n}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\mathrm{then}\:\mathrm{for} \\ $$$$\omega^{{x}} +\omega^{{y}} +\omega^{{z}} =\mathrm{0} \\ $$$$\mathrm{as}\:\mathrm{shown}\:\mathrm{above},\:\mathrm{them}\:\mathrm{need}\:\mathrm{to}\:\mathrm{have}\:\mathrm{a}\:\mathrm{angle} \\ $$$$\mathrm{of}\:\mathrm{120}°\:\mathrm{betwen}\:\mathrm{them},\:\mathrm{wich}\:\mathrm{imply}\:\mathrm{that} \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{three}\:\mathrm{roots}\:\mathrm{apear},\:\mathrm{without}\:\mathrm{loss}\:\mathrm{of}\:\mathrm{generaly} \\ $$$$\mathrm{take} \\ $$$${x}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$${y}\equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$${z}\equiv\mathrm{2}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\mathrm{them} \\ $$$${x}+{y}+{z}\equiv\mathrm{0}+\mathrm{1}+\mathrm{2}\equiv\mathrm{3}\equiv\mathrm{0}\left(\mathrm{mod}\:\mathrm{3}\right) \\ $$$$\mathrm{wich}\:\mathrm{imply}\:\mathrm{that} \\ $$$$\mathrm{3}\mid\left({x}+{y}+{z}\right) \\ $$
Commented by Rasheed Soomro last updated on 23/Aug/15

$$\:\mathrm{THANKS}.\:\mathrm{Fully}\:\:\mathrm{logical}\:\:\mathrm{and}\:\mathrm{full}\:\mathrm{of}\:\mathrm{knowledge}. \\ $$$$\mathrm{But}\:\mathrm{too}\:\mathrm{technical}!\:\mathrm{Long}\:\mathrm{tour}\:\mathrm{of}\:\mathrm{logic}! \\ $$$$\mathrm{Could}\:\mathrm{there}\:\mathrm{be}\:\mathrm{a}\:\mathrm{simple}{r}\:\:\mathrm{answer}? \\ $$$$ \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 23/Aug/15
![x,y,z ∈ Z (given) All the integers wrt modulo 3 are of three types 3k, 3k+1, 3k+2 . So suppose each of x, y, z is one of above types. It can easily be shown that ω^x +ω^y +ω^z =0 ⇒ { ((x, y, z all are of different types)),(((wrt modulo 3))) :} [If two or three are of same type ω^x +ω^y +ω^z ≠0.] Let one of x, y, z is equal to 3l, another is equal to 3m+1 and remaining is equal to 3n+2 ω^x +ω^y +ω^z = ω^(3l) +ω^(3m+1) +ω^(3n+2) =1+ω+ω^2 =0 ⇒ { x+y+z= 3l+(3m+1)+(3n+2) = 3l+3m+3n+3=3(l+m+n+1) This implies that 3 ∣ (x+y+z) } Counter examples that prove that converse is not true: 1) Each of x,y,z is of 3k type. x+y+z=3l+3m+3n=3(l+m+n) 3 ∣ (x+y+z) But ω^x +ω^y +ω^z =ω^(3l) +ω^(3m) +ω^(3n) =1+1+1=3≠0 2) Each of x,y,z is of 3k+1 type. 3) Each of x,y,z is of 3k+2 type.](Q1591.png)
$$\:\:\:\:\:\:\:\:\mathrm{x},\mathrm{y},\mathrm{z}\:\in\:\mathbb{Z}\:\left(\mathrm{given}\right) \\ $$$$\mathrm{All}\:\mathrm{the}\:\mathrm{integers}\:\mathrm{wrt}\:\mathrm{modulo}\:\mathrm{3}\:\mathrm{are}\:\mathrm{of}\:\mathrm{three}\:\mathrm{types}\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{3k},\:\mathrm{3k}+\mathrm{1},\:\mathrm{3k}+\mathrm{2}\:. \\ $$$$\:\mathrm{So}\:\mathrm{suppose}\:\mathrm{each}\:\mathrm{of}\:\mathrm{x},\:\mathrm{y},\:\mathrm{z}\:\mathrm{is}\:\mathrm{one}\:\mathrm{of}\:\mathrm{above}\:\mathrm{types}. \\ $$$$\mathrm{It}\:\mathrm{can}\:\mathrm{easily}\:\mathrm{be}\:\mathrm{shown}\:\mathrm{that}\: \\ $$$$\:\:\:\:\:\:\:\:\omega^{\mathrm{x}} +\omega^{\mathrm{y}} +\omega^{\mathrm{z}} =\mathrm{0}\:\:\Rightarrow\begin{cases}{\mathrm{x},\:\mathrm{y},\:\mathrm{z}\:\mathrm{all}\:\:\mathrm{are}\:\mathrm{of}\:\mathrm{different}\:\mathrm{types}}\\{\left(\mathrm{wrt}\:\mathrm{modulo}\:\mathrm{3}\right)}\end{cases}\: \\ $$$$\left[\mathrm{If}\:\mathrm{two}\:\mathrm{or}\:\mathrm{three}\:\:\mathrm{are}\:\mathrm{of}\:\mathrm{same}\:\mathrm{type}\:\omega^{\mathrm{x}} +\omega^{\mathrm{y}} +\omega^{\mathrm{z}} \neq\mathrm{0}.\right] \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{Let}\:\mathrm{one}\:\mathrm{of}\:\:\mathrm{x},\:\mathrm{y},\:\mathrm{z}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{3}{l},\:\mathrm{another}\:\mathrm{is}\:\mathrm{equal} \\ $$$$\mathrm{to}\:\mathrm{3}{m}+\mathrm{1}\:\mathrm{and}\:\mathrm{remaining}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{3}{n}+\mathrm{2} \\ $$$$\:\:\:\:\omega^{\mathrm{x}} +\omega^{\mathrm{y}} +\omega^{\mathrm{z}} =\:\omega^{\mathrm{3}{l}} +\omega^{\mathrm{3}{m}+\mathrm{1}} +\omega^{\mathrm{3}{n}+\mathrm{2}} =\mathrm{1}+\omega+\omega^{\mathrm{2}} =\mathrm{0}\:\Rightarrow \\ $$$$\left\{\right. \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{x}+\mathrm{y}+\mathrm{z}=\:\mathrm{3}{l}+\left(\mathrm{3}{m}+\mathrm{1}\right)+\left(\mathrm{3}{n}+\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{3}{l}+\mathrm{3}{m}+\mathrm{3}{n}+\mathrm{3}=\mathrm{3}\left({l}+{m}+{n}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{This}\:\mathrm{implies}\:\mathrm{that}\:\:\:\:\:\:\:\:\mathrm{3}\:\mid\:\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left.\right\} \\ $$$$\mathrm{Counter}\:\mathrm{examples}\:\mathrm{that}\:\mathrm{prove}\:\mathrm{that}\:\:\mathrm{converse}\:\mathrm{is}\:\mathrm{not}\:\mathrm{true}: \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\right)\:\:\mathrm{Each}\:\mathrm{of}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{is}\:\mathrm{of}\:\mathrm{3k}\:\mathrm{type}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{3}{l}+\mathrm{3}{m}+\mathrm{3}{n}=\mathrm{3}\left({l}+{m}+{n}\right) \\ $$$$\mathrm{3}\:\mid\:\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\:\mathrm{But}\:\omega^{\mathrm{x}} +\omega^{\mathrm{y}} +\omega^{\mathrm{z}} =\omega^{\mathrm{3}{l}} +\omega^{\mathrm{3}{m}} +\omega^{\mathrm{3}{n}} =\mathrm{1}+\mathrm{1}+\mathrm{1}=\mathrm{3}\neq\mathrm{0} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\right)\:\mathrm{Each}\:\mathrm{of}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{is}\:\mathrm{of}\:\:\mathrm{3k}+\mathrm{1}\:\:\mathrm{type}. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}\right)\:\mathrm{Each}\:\mathrm{of}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{is}\:\mathrm{of}\:\:\mathrm{3k}+\mathrm{2}\:\:\mathrm{type}. \\ $$
